题意 : 给你若干个点,让你找最小的正方形覆盖这所有的点。输出面积。
思路 : 三分枚举正方形两对边的距离,然后求出最大,本题用的是旋转正方形,也可以用旋转点,即点的相对位置不变。
正方形从0度到180度变化的过程中,把所有点覆盖,面积肯定是有一个最小峰值,是一个凸函数。因此可以用三分法解决。这里有一个难点就是已知两个定点的x,y坐标,过这两个点做两条平行线,平行线并与x轴成d度的角,怎么算出两条平行线的距离。
d1 = fabs(cos(d)*(yi-yj)-sin(d)*(xi-xj));
d2 = fabs*(sin(d)*(yi-yj)+cos(d)*(xi-xj));

1 #include <iostream> 2 #include <cstdio> 3 #include <cmath> 4 #define eps 1e-9 5 6 using namespace std; 7 8 int T,n; 9 int x[1000],y[1000]; 10 11 double calc(double d) 12 { 13 double dis1,dis2,dis; 14 dis = 0.0; 15 for(int i = 1 ; i < n ; i ++) 16 { 17 for(int j = i+1 ; j <= n ; j++) 18 { 19 dis1 = fabs(cos(d)*(y[i]-y[j])-sin(d)*(x[i]-x[j])); 20 dis2 = fabs(sin(d)*(y[i]-y[j])+cos(d)*(x[i]-x[j])); 21 dis = max(dis,max(dis1,dis2) ) ; 22 } 23 } 24 return dis*dis; 25 } 26 int main() 27 { 28 double l,r,mid,midmid; 29 double s1,s2; 30 cin>>T; 31 for(int k = 0 ; k < T ; k++) 32 { 33 cin>>n; 34 for(int i = 1 ; i <= n ; i++) 35 cin>>x[i]>>y[i]; 36 l = 0.0; 37 r = acos(-1.0)/2; 38 while(r-l >= eps) 39 { 40 mid = (l + r) / 2 ; 41 midmid = (mid + r) / 2 ; 42 s1 = calc(mid) ; 43 s2 = calc(midmid) ; 44 if(s1 < s2) 45 r = midmid ; 46 else l = mid ; 47 } 48 printf("%.2lf\n",min(s1,s2)); 49 } 50 return 0; 51 }
三分算法解决凸形或者凹形函数的极值;
二分解决具有单调性的函数的极值;
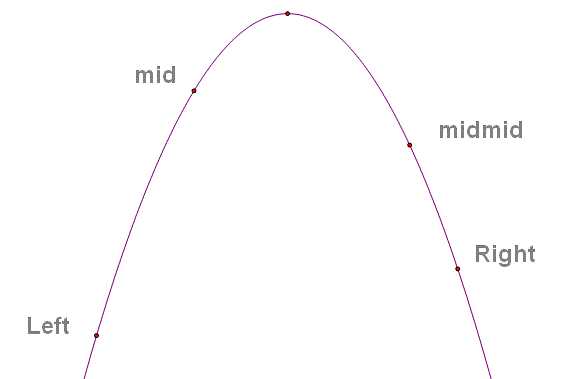
mid = (Left + Right) / 2
midmid = (mid + Right) / 2;
如果mid靠近极值点,则Right = midmid;
否则(即midmid靠近极值点),则Left = mid;
程序模版如下:
double cal(Type a) { /* 根据题目的意思计算 */ }
1 void solve() 2 { 3 double Left, Right; 4 double mid, midmid; 5 double mid_value, midmid_value; 6 Left = MIN; Right = MAX; 7 while (Left + EPS <= Right) 8 { 9 mid = (Left + Right) / 2; 10 midmid = (mid + Right) / 2; 11 if (cal(mid)>=cal(midmid)) 12 13 Right = midmid; 14 else Left = mid; 15 } 16 }
我搜索的三分算法的题目:HDU :3400 2298 4454 2438 3756
POJ: 3301 3737
ZOJ: 3203
POJ 3301 Texas Trip (三分),布布扣,bubuko.com
原文:http://www.cnblogs.com/luyingfeng/p/3895820.html