本节为手撕代码系列之第一弹,主要来手撕排序算法,主要包括以下几大排序算法:
直接插入排序
冒泡排序
选择排序
快速排序
希尔排序
堆排序
归并排序
【算法思想】
每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
【代码实现】
# 直接插入排序 def insert_sort(arr): length = len(arr) for i in range(length): k = i for j in range(k,0,-1): if arr[j]<arr[j-1]: t = arr[j] arr[j]=arr[j-1] arr[j-1]=t arr = [4,3,0,-1] insert_sort(arr) print(arr)
【算法思想】
对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序。
【代码实现】
# 冒泡排序 def bubbleSort(arr): length = len(arr) for i in range(length-1): flag = True for j in range(length-i-1): if arr[j]>arr[j+1]: t = arr[j] arr[j]=arr[j+1] arr[j+1]=t flag = False if flag: break arr = [6,-2,0,9] bubbleSort(arr) print(arr)
【算法思想】
每一趟从待排序的数据元素中选择最小(或最大)的一个元素作为首元素,直到所有元素排完为止,简单选择排序是不稳定排序。
【代码实现】
def selectSort(arr): length = len(arr) for i in range(length-1): min = i for j in range(i+1,length): if arr[min]>arr[j]: min=j if min!=i: t = arr[i] arr[i]=arr[min] arr[min]=t arr = [6,-2,0,9] selectSort(arr) print(arr)
【算法思想】
快速排序思想----分治法。
先从数列中取出一个数作为基准数。
分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
再对左右区间重复第二步,直到各区间只有一个数。
每次划分得到,枢椎的左边比它小,右边比它大。
【代码实现】
def quickSort(arr,left,right): # 递归终止条件 if left>right: return pivot = arr[left] i = left j = right while i<j: while i<j and arr[j]>=pivot: j-=1 while i<j and arr[i]<=pivot: i+=1 if i<j: t = arr[i] arr[i] = arr[j] arr[j] = t # 放入枢椎 arr[left] = arr[i] arr[i]=pivot # 递归调用左区域 quickSort(arr,left,i-1) # 递归调用右区域 quickSort(arr,i+1,right) arr = [6,-2,0,9] quickSort(arr,0,len(arr)-1) print(arr)
【算法思想】
该算法也被称为:缩小增量排序。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
【代码实现】
# 希尔排序 def shellSort(arr): length = len(arr) # 设置初始增量 gap = length//2 while gap>0: # 从第gap个元素,逐个对其所在组进行直接插入排序 for i in range(gap,length): j = i while j-gap>=0 and arr[j]<arr[j-gap]: t = arr[j] arr[j] = arr[j-gap] arr[j-gap] = t j-=gap gap//=2 arr = [6,-2,0,9] shellSort(arr) print(arr)
【算法思想】
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。
基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;(升序方法)
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
【代码实现】
class HeapSort: def heapSort(self, nums): length = len(nums) # 从后往前遍历,交换堆顶与最后叶子节点,并依次调整堆,重复操作 for j in range(length-1,0,-1): # 获取堆顶元素(获取同时,调整堆) firstNum = self.adjustHeap(nums,j+1) # 交换最后一个叶子节点与堆顶元素 temp = nums[j] nums[j] = firstNum nums[0] = temp return nums # 调整堆(最大堆),每次返回最大堆顶元素 def adjustHeap(self,nums,length): # 最后一个非叶节点 i = length//2 -1 # 从最后一个非叶节点开始调整,构成最大堆 while i>=0: temp = nums[i] k = 2*i+1 while k<length: if k+1<length and nums[k]<nums[k+1]: k+=1 if nums[k]>temp: nums[i]=nums[k] i=k else: break k=2*k+1 nums[i] = temp i-=1 return nums[0] s = HeapSort() nums = [8,9,7,10] t = s.heapSort(nums) print(t)
【算法思想】
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
【代码实现】
def mergeSort(nums): if len(nums)<=1: return nums mid = len(nums)//2 left = mergeSort(nums[:mid]) right = mergeSort(nums[mid:]) return merge(left,right) def merge(left,right): result = [] i,j = 0,0 while i<len(left) and j<len(right): if left[i]<=right[j]: result.append(left[i]) i+=1 else: result.append(right[j]) j+=1 if i<len(left): result+=left[i:] if j<len(right): result+=right[j:] return result nums = [5,3,0,6,1,4] t = mergeSort(nums) print(t)
来自于wx公众号“光城”。
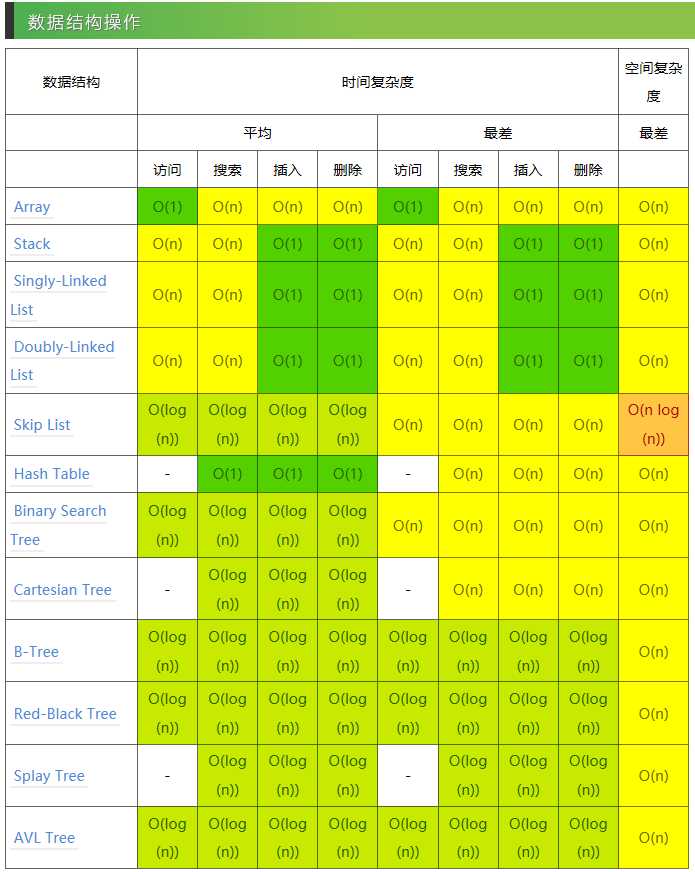
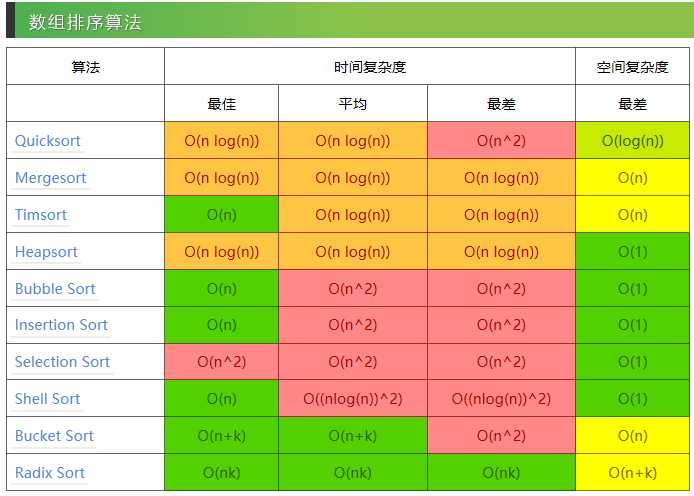
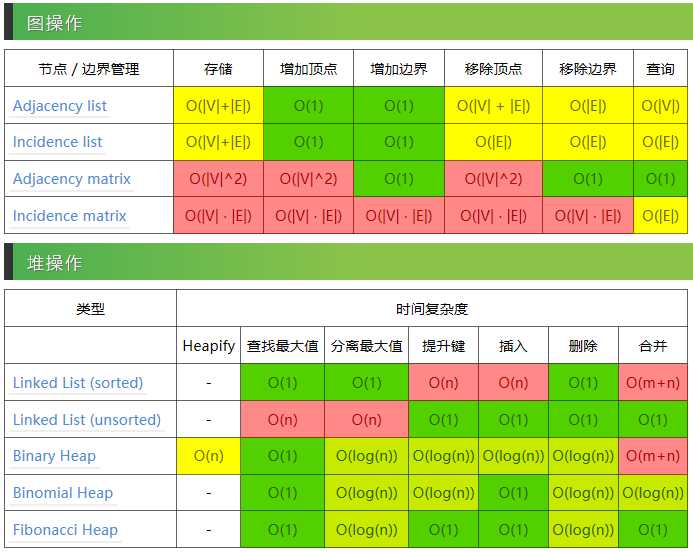
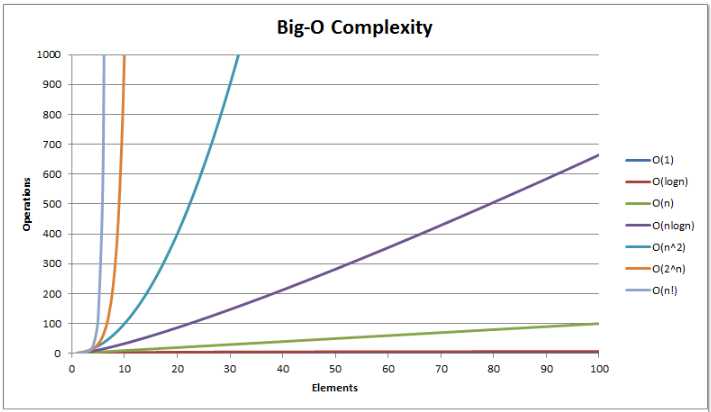
基本算法复杂度:
参考来源:https://linux.cn/article-7480-1.html

原文:https://www.cnblogs.com/nicetoseeyou/p/10512700.html