写一点自己对码间串扰的理解。。(大白话)
码间干扰是数字通信系统中除噪声干扰之外最主要的干扰,它与加性的噪声干扰不同,是一种乘性的干扰。造成码间干扰的原因有很多,实际上,只要传输信道的频带是有限的,就会造成一定的码间干扰。
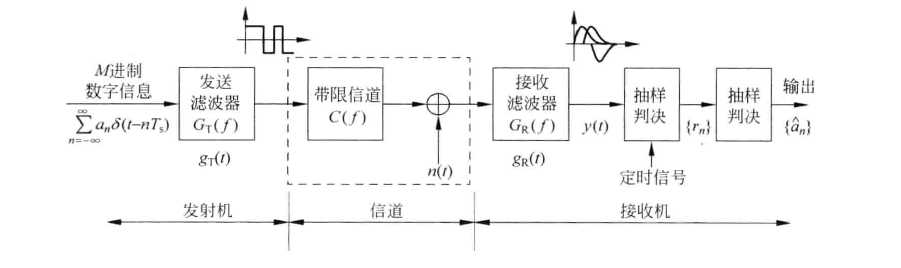
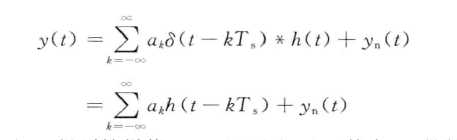
对y(t)信号进行抽样判决,设抽样值t=nTs ,那么 抽样值{rn} 表示为
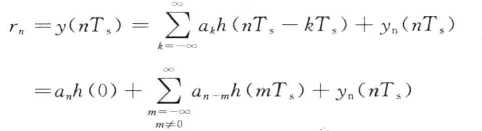
经过变形后 除了h(0)之外的都是干扰,第二项就是码间干扰(an数字所引起的波形值为h(0)其他的都是有其他码元引起的),所以我们要设计h(t)是码间串扰为零。
在时域 在频域(奈奎斯特)
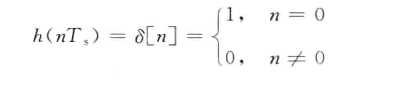
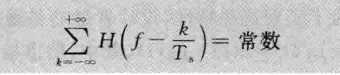
从上式中我们能联想起一种特殊h(f)即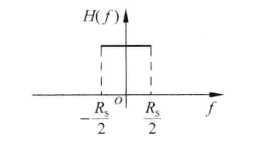
这种H(f)的带宽为W(我们所说的带宽就是H(f)的带宽当然它由信道带宽来决定)
上面的系统是最小带宽系统即 W = R/2 ,但是这个像理想低通滤波器的系统频谱这么尖锐,物理不可实现的。即使实现了在他的时域部分尾巴的震动是很激烈的,如果我们的定时制作不好系统的性能一样很差劲。
所以来讲我们设计系统时要从整体来考虑,不是仅仅考虑发端或者收端。h(f)是一个整体;而且我们也要考虑抽样与判决这样设计出来的系统才能完美;
现在说一下:如果时域我们发方脉冲,匹配滤波器也将是方脉冲,如果带宽无限那么我们就不会有码间串扰,实际上要带限的,所以不可取
如果把发送滤波器和匹配滤波器都设计成频域为低通的,由于物理不可实现的所以也不可取;
那么我们该怎么设计呢?在实际中我们往往把他设计成H(f)为升余弦;
原文:https://www.cnblogs.com/yangzhanxiang/p/10527021.html