题意
Problem 4572. -- [Scoi2016]围棋4572: [Scoi2016]围棋
Time Limit: 50 Sec Memory Limit: 512 MB
Submit: 252 Solved: 154
[Submit][Status][Discuss]Description
近日,谷歌研发的围棋AI—AlphaGo以4:1的比分战胜了曾经的世界冠军李世石,这是人工智能领域的又一里程碑。
与传统的搜索式AI不同,AlphaGo使用了最近十分流行的卷积神经网络模型。在卷积神经网络模型中,棋盘上每一
块特定大小的区域都被当做一个窗口。例如棋盘的大小为5×6,窗口大小为2×4,那么棋盘中共有12个窗口。此外
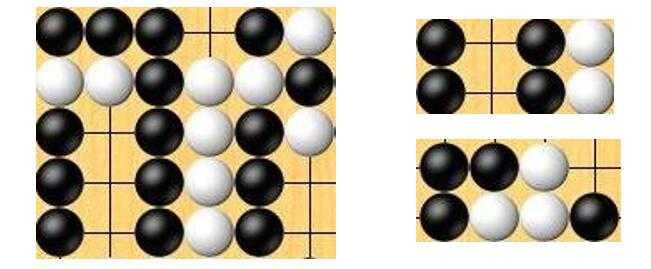
,模型中预先设定了一些模板,模板的大小与窗口的大小是一样的。下图展现了一个5×6的棋盘和两个2×4的模板
。对于一个模板,只要棋盘中有某个窗口与其完全匹配,我们称这个模板是被激活的,否则称这个模板没有被激活
。例如图中第一个模板就是被激活的,而第二个模板就是没有被激活的。我们要研究的问题是:对于给定的模板,
有多少个棋盘可以激活它。为了简化问题,我们抛开所有围棋的基本规则,只考虑一个n×m的棋盘,每个位置只能
是黑子、白子或无子三种情况,换句话说,这样的棋盘共有3n×m种。此外,我们会给出q个2×c的模板。我们希望
知道,对于每个模板,有多少种棋盘可以激活它。强调:模板一定是两行的。
Input
输入数据的第一行包含四个正整数n,m,c和q,分别表示棋盘的行数、列数、模板的列数和模板的数量。随后2×q
行,每连续两行描述一个模板。其中,每行包含c个字符,字符一定是‘W’,‘B’或‘X’中的一个,表示白子、
黑子或无子三种情况的一种。N<=100,M<=12,C<=6,Q<=5
Output
输出应包含q行,每行一个整数,表示符合要求的棋盘数量。由于答案可能很大,你只需要输出答案对1,000,000,007取模后的结果即可。
Sample Input
3 1 1 2
B
W
B
B
Sample Output
6
5
HINT
Source
[Submit][Status][Discuss]?
HOME
Back
无图差评,样例只有一组差评,数据范围没给全差评。
分析
考虑反面,用状压DP求出不合法的方案数,用\(3^{n*m}\)减去它就行了。
如果模板串只有一行,那么状态显然是\(f[i][j]\),表示长度为\(i\)匹配到状态\(j\)未出现模板串的方案数。
考虑多了一行怎么做。显然不能两行都匹配上了,但是只有一行匹配上是可行的。那么就要记录二进制状态\(S\)表示上一行每个位置作为开头是否完全匹配第一个串。为了方便转移\(S\),还要记录当前位置匹配到了第一个串的哪个位置。
那么设\(f[i][j][S][x][y]\)表示填到了\((i,j)\),上一行每个位置作为开头是否完全匹配第一个串的状态为\(S\),与第一个串kmp匹配到了\(x\),与第二个串kmp匹配到了\(y\)的方案数。然后直接加法转移即可。实现的时候不用记录状态\((i,j)\)
可以预处理出自动机,加速匹配。
时间复杂度\(O(nm2^{m-c+1}c^2)\),最后那个测试点是5e6.
代码
#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;
rg char ch=getchar();
while(!isdigit(ch)){
if(ch=='-') w=-1;
ch=getchar();
}
while(isdigit(ch))
data=data*10+ch-'0',ch=getchar();
return data*w;
}
template<class T>il T read(rg T&x){
return x=read<T>();
}
typedef long long ll;
co int mod=1e9+7;
int n,m,c,T,nxt[7],ta[6][3],tb[6][3],na,nb;
char a[8],b[8];
int id(char x) {return x=='B'?0:(x=='W'?1:2);}
int U,f[1024][6][6],g[1024][6][6],ans;
void up(int&x,int y) {x+=y;if(x>=mod)x-=mod;}
void clear() {for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)g[S][x][y]=0;}
void copy() {for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)f[S][x][y]=g[S][x][y];}
int main(){
// freopen(".in","r",stdin),freopen(".out","w",stdout);
read(n),read(m),read(c),read(T);
while(T--){
scanf("%s%s",a+1,b+1);
for(int i=1;i<=c;++i)a[i]=id(a[i]),b[i]=id(b[i]);
for(int j=nxt[1]=0,i=2;i<=c;nxt[i++]=j){
while(j&&a[j+1]!=a[i]) j=nxt[j];
if(a[j+1]==a[i]) ++j;
}
na=nxt[c];
for(int i=0;i<c;++i)for(int j=0,k;j<3;++j){
for(k=i;k&&a[k+1]!=j;k=nxt[k]);
if(a[k+1]==j) ++k;
ta[i][j]=k;
}
for(int j=nxt[1]=0,i=2;i<=c;nxt[i++]=j){
while(j&&b[j+1]!=b[i]) j=nxt[j];
if(b[j+1]==b[i]) ++j;
}
nb=nxt[c];
for(int i=0;i<c;++i)for(int j=0,k;j<3;++j){
for(k=i;k&&b[k+1]!=j;k=nxt[k]);
if(b[k+1]==j) ++k;
tb[i][j]=k;
}
U=1<<(m-c+1);
for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)f[S][x][y]=0;
for(int i=f[0][0][0]=1;i<=n;++i){
clear();
for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)
if(f[S][x][y]) up(g[S][0][0],f[S][x][y]);
copy();
for(int j=1;j<=m;++j){
clear();
for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y)
if(f[S][x][y]) for(int k=0,A,B,E;k<3;++k){
E=S;
if(j>=c) if(S>>(j-c)&1) E^=1<<(j-c); // init
A=ta[x][k];
if(A==c) E|=1<<(j-c),A=na;
B=tb[y][k];
if(B==c){
if(S>>(j-c)&1) continue;
B=nb;
}
up(g[E][A][B],f[S][x][y]);
}
copy();
}
}
ans=1;
for(int i=n*m;i;--i) ans=3LL*ans%mod;
for(int S=0;S<U;++S)for(int x=0;x<c;++x)for(int y=0;y<c;++y) up(ans,mod-f[S][x][y]);
printf("%d\n",ans);
}
return 0;
}
加强版
由于那个状态\(S\)跟棋子无关,所以可以增加棋子种类。另外可以规定某些位置不能填什么,某些位置必须填什么。
BZOJ4572 [Scoi2016]围棋
原文:https://www.cnblogs.com/autoint/p/10533089.html



