一个渣渣的再次分享：

标题：圆周率

数学发展历史上，圆周率的计算曾有许多有趣甚至是传奇的故事。其中许多方法都涉及无穷级数。

图1.png中所示，就是一种用连分数的形式表示的圆周率求法。

下面的程序实现了该求解方法。实际上数列的收敛对x的初始值 并不敏感。

结果打印出圆周率近似值（保留小数点后4位，并不一定与圆周率真值吻合）。

double x = 111;
for(int n = 10000; n>=0; n--){
int i = 2 * n + 1;
x = 2 + (i*i / x);
}

System.out.println(String.format("%.4f", ______________));

图一在此：

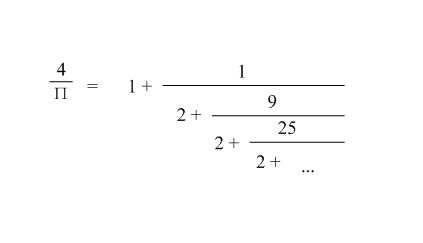
结果（自动加红色）：4/（x-1）

一渣一总结：按照他的想法n从10000，不如到这想从0开始，闯一闯

圆周率

原文：https://www.cnblogs.com/zhazhaboke/p/10533676.html