动态规划

一. 动态规划概念

当年学习算法的动态规划部分时，就觉得一个字，难。至今过去一年左右，再次捡起来。
它可以说是算法的精髓，少了它便少了一份美。而它确实是独一无二的存在，它不属于也不是一个特定的算法，而是一个思想，一种手段。

接下来我们举个例子说明下什么叫动态规划，理解下状态和状态转移方程，理解下最优子结构。

数字三角形

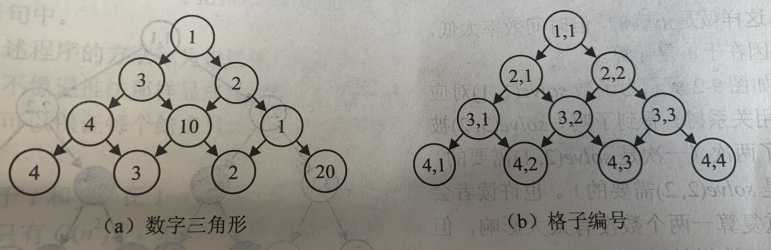
如果我们要求从第一行开始，每次往下走一格，可以往左，也可以往右，直到走到最下行，把沿途经过的数全部加起来，如何走才能使得这个数尽量大？
解法

把当前的位置(i,j)看成是一种状态，然后定位(i,j)的指标函数d(i,j)为从格子(i,j)出发时能得到的最大和(包括自身的值)，这样题目要求就转化成求d(1,1)

状态转移方程：d(i,j)=a(i,j)+max{d(i+1,j),d(i+1,j+1)}

最优子结构：(i,j)接下来如果往左走，那么就是a(i,j)加上从(i+1,j)位置出发的最大总和，注意这里必须要求(i+1,j)最大总和，这个性质称为最优子结构。换一种说法就是全局最优解包含局部最优解

二. 实现的三种方法

方法1：递归

int solve(int i,int j){
    return a[i][j]+(i==n?0:max(solve(i+1,j),solve(i+1,j+1)));
}

解释

1. 首先该指出此方法不好，时间效率太低，原因在于重复计算。

2. 本程序用到了一个三目运算符，旨在区别最后一行与其他行的运算区别，最后一行就是本身状态值就是了。

   方法2：递推

   方法3：记忆化

初见动态规划

原文：https://www.cnblogs.com/MarkKobs-blog/p/10536210.html