我们定义一棵树的删除序列为:每一次将树中编号最小的叶子删掉,将该节点编号加入到当前序列的最末端,最后只剩下一个节点时将该节点的编号加入到结尾。
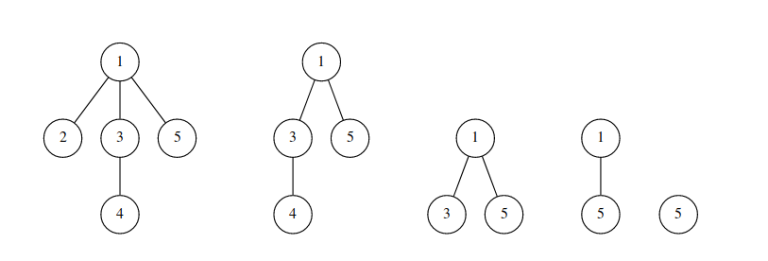
例如对于上图中的树,它的删除序列为:2 4 3 1 5
现在给出一棵\(n\)个节点的树,有\(m\)次操作:
\(up\) \(v\):将\(v\)号节点的编号变为当前所有节点编号的\(\max + 1\)
\(when\) \(v\):查询\(v\)在当前树的删除序列中是第几号元素
\(compare\) \(u\) \(v\):查询\(u\)和\(v\)在当前树的删除序列中谁更靠前
放火烧山,牢底坐穿
首先我们考虑一下,设当前树上优先度最高的点为\(u\),此时一个\(up\)操作,使得\(v\)成为了优先度最高的点,那么这棵树烧起来的时候会发生什么事
首先\(uv\)之间这条路肯定会最后才烧着,而且是从\(u\)烧到\(v\),而其它所有节点烧的相对顺序都是不变的
那么可以理解为,我们定义一个时间戳\(tim\),每次\(up\)操作的时候\(++tim\),并记录一下这个时间戳路径的起点\(u\),然后把\(uv\)路径上全都覆盖上这个时间戳。那么,一个节点第几个被烧呢?显然就是所有时间戳小于它的点的点数,再加上它到自己时间戳的起点\(u\)的距离
每一次都是区间覆盖,有没有让你想到什么呢?
对,这很像珂朵莉树。我们可以先树剖,对于每一条重链,维护一个\(set\),\(set\)里维护这条重链上的颜色区间。那么一次区间覆盖只要把旧的区间删去,并加入新的区间就行了。不过因为要维护每种颜色的点的个数,所以我们可能还需要用一个树状数组,再删除和插入区间的时候维护一下点的个数
还有个问题是我们需要算出一开始的答案,直接把每个点暴力\(up\)就行了
虽然说着像珂朵莉树不过这里的复杂度应该是严格的。每一次路径修改会被拆成\(O(\log n)\)个区间,每个被拆出来的区间最多插入一次删除一次。以及我们中间有可能需要把一个区间拆成两半,一次是询问的时候要把一个点拆出来看看它的时间戳是啥,那么这一部分拆出的区间总数是\(O(n)\)的。还有就是我们插入区间的时候有可能会拆掉区间,不过这种情况下拆出的区间最多一个,所以一次路径覆盖最多会拆出\(O(\log n)\)的区间,和前面的复杂度相同,再加上\(set\)和树状数组,时间复杂度应该是\(O(n\log^2 n)\)(大概没算错?)
//minamoto
#include<bits/stdc++.h>
#define R register
#define IT set<node>::iterator
#define fp(i,a,b) for(R int i=(a),I=(b)+1;i<I;++i)
#define fd(i,a,b) for(R int i=(a),I=(b)-1;i>I;--i)
#define go(u) for(int i=head[u],v=e[i].v;i;i=e[i].nx,v=e[i].v)
template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,1:0;}
using namespace std;
char buf[1<<21],*p1=buf,*p2=buf;
inline char getc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++;}
int read(){
R int res,f=1;R char ch;
while((ch=getc())>'9'||ch<'0')(ch=='-')&&(f=-1);
for(res=ch-'0';(ch=getc())>='0'&&ch<='9';res=res*10+ch-'0');
return res*f;
}
int read(char *s){
R int len=0;R char ch;while(((ch=getc())>'z'||ch<'a'));
for(s[++len]=ch;(ch=getc())>='a'&&ch<='z';s[++len]=ch);
return s[len+1]='\0',len;
}
char sr[1<<21],z[20];int C=-1,Z=0;
inline void Ot(){fwrite(sr,1,C+1,stdout),C=-1;}
void print(R int x){
if(C>1<<20)Ot();if(x<0)sr[++C]='-',x=-x;
while(z[++Z]=x%10+48,x/=10);
while(sr[++C]=z[Z],--Z);sr[++C]='\n';
}
const int N=5e5+5;
struct node{
int l,r,c;
node(){}
node(R int ll,R int rr=-1,R int cc=N){l=ll,r=rr,c=cc;}
inline bool operator <(const node &b)const{return l<b.l;}
};set<node>pool[N],*s[N];
struct eg{int v,nx;}e[N<<1];int head[N],tot;char t[25];
int dfn[N],sz[N],son[N],fa[N],top[N],dep[N],bg[N],c[N],mx[N];
int n,m,cnt,tim,las;
inline void add(R int u,R int v){e[++tot]={v,head[u]},head[u]=tot;}
inline void upd(R int x,R int y){for(;x<N;x+=x&-x)c[x]+=y;}
inline int ask(R int x){R int res=0;for(;x;x-=x&-x)res+=c[x];return res;}
IT split(set<node> *s,int pos){
IT it=s->lower_bound(node(pos));
if(it!=s->end()&&it->l==pos)return it;
--it;int l=it->l,r=it->r,c=it->c;
s->erase(it),s->insert(node(l,pos-1,c));
return s->insert(node(pos,r,c)).first;
}
void ins(set<node> *s,int l,int r,int c){
IT itr=split(s,r+1),itl=split(s,l);
for(IT it=itl;it!=itr;++it)upd(it->c,-(it->r-it->l+1));
upd(c,r-l+1);
s->erase(itl,itr),s->insert(node(l,r,c));
}
void dfs1(int u){
sz[u]=1,dep[u]=dep[fa[u]]+1;
go(u)if(v!=fa[u]){
fa[v]=u,dfs1(v),sz[u]+=sz[v];
sz[v]>sz[son[u]]?son[u]=v:0;
}
}
void dfs2(int u,int t){
top[u]=t,mx[u]=dfn[u]=++cnt;
if(son[u])dfs2(son[u],t),cmax(mx[u],mx[son[u]]);
if(u==t)s[u]=&pool[u],s[u]->insert(node(dfn[u],mx[u]+1));
go(u)if(!top[v])dfs2(v,v);
}
int LCA(int u,int v){
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
u=fa[top[u]];
}
return dep[u]<dep[v]?u:v;
}
inline int dis(R int u,R int v){return dep[u]+dep[v]-(dep[LCA(u,v)]<<1)+1;}
void update(int u,int v){
bg[++tim]=u;
while(top[u]!=top[v]){
if(dep[top[u]]<dep[top[v]])swap(u,v);
ins(s[top[u]],dfn[top[u]],dfn[u],tim);
u=fa[top[u]];
}
if(dep[u]>dep[v])swap(u,v);
ins(s[top[u]],dfn[u],dfn[v],tim);
}
int query(int u){
int c=split(s[top[u]],dfn[u])->c;
return ask(c-1)+dis(u,bg[c]);
}
int main(){
// freopen("testdata.in","r",stdin);
n=read(),m=read();
for(R int i=1,u,v;i<n;++i)u=read(),v=read(),add(u,v),add(v,u);
dfs1(1),dfs2(1,1),las=n;
fp(i,1,n-1)update(i,i+1);
for(R int T=1,u,v;T<=m;++T){
read(t),u=read(),t[1]=='c'?v=read():0;
switch(t[1]){
case 'u':update(las,u),las=u;break;
case 'w':print(query(u));break;
case 'c':print(query(u)<query(v)?u:v);break;
}
}
return Ot(),0;
}CF1137F Matches Are Not a Child's Play(树链剖分)
原文:https://www.cnblogs.com/bztMinamoto/p/10537308.html