给定一正整数\(N \in \mathbb{N}^*\),试快速找到它的一个因数。
很久很久以前,我们曾学过试除法来解决这个问题。很容易想到因数是成对称分布的:即\(N\)的所有因数可以被分成两块:\([1,\sqrt(N)]\)和\([\sqrt(N),N]\).这个很容易想清楚,我们只需要把区间\([1,\sqrt(N)]\)扫一遍就可以了,此时试除法的时间复杂度为\(O(\sqrt(N))\).
对于\(N \geqslant 10^{18}\)的数据,这个算法运行起来无意是非常糟糕的.我们希望有更快的算法,比如\(O(1)\)级别的?
对于这样的算法,一个比较好的想法是去设计一个随机程序,随便猜一个因数.如果你运气好,这个程序的时间复杂度下限为\(o(1)\).但对于一个\(N \geqslant 10^{18}\)的数据,这个算法给出答案的概率是\(\frac{1}{1000000000000000000}\).当然,如果在\([1,\sqrt(N)]\)里面猜,成功的可能性会更大.
那么,有没有更好的改进算法来提高我们猜的准确率呢?
我们来考虑这样一种情况:在\([1,1000]\)里面取一个数,取到我们想要的数(比如说,\(42\)),成功的概率是多少呢?显然是\(\frac{1}{1000}\).
一个不行就取两个吧:随便在\([1,1000]\)里面取两个数.我们想办法提高准确率,就取两个数的差值绝对值.也就是说,在\([1,1000]\)里面任意选取两个数\(i , j\),问\(|i-j|=42\)的概率是多大?答案会扩大到\(\frac{1}{500}\)左右,也就是将近扩大一倍.机房的gql大佬给出了简证:\(i\)在\([1,1000]\)里面取出一个正整数的概率是\(100\%\),而取出\(j\)满足\(|i-j|=42\)的概率差不多就是原来的一倍:\(j\)取\(i-42\)和\(i+42\)都是可以的.
这给了我们一点启发:这种"组合随机采样"的方法是不是可以大大提高准确率呢?
这个便是生日悖论的模型了.假如说一个班上有k个人,如果找到一个人的生日是4月2日,这个概率的确会相当低.但是如果单纯想找到两个生日相同的人,这个概率是不是会高一点呢?
可以暴力证明:如果是\(k\)个人生日互不相同,则概率为:\(p=\frac{365}{365}\cdot\frac{364}{365}\cdot\frac{363}{365}\cdot\dots\cdot\frac{365-k+1}{365}\) ,故生日有重复的现象的概率是:\(\text{P}(k)=1-\prod\limits_{i=1}^{k}{\frac{365-i+1}{365}}\).
我们随便取一个概率:当\(P(k) \geqslant \frac{1}{2}\)时,解得\(k \gtrsim 23\).这意味着一个有23个人组成的班级中,两个人在同一天生日的概率至少有\(50\%\)!当k取到60时,\(\text{P}(k) \approx 0.9999\).这个数学模型和我们日常的经验严重不符.这也是"生日悖论"这个名字的由来.
生日悖论的实质是:由于采用"组合随机采样"的方法,满足答案的组合比单个个体要多一些.这样可以提高正确率.
我们不妨想一想:如何通过组合来提高正确率呢?有一个重要的想法是:最大公约数一定是某个数的约数.也就是说,\(\forall k \in \mathbb{N}^* , \gcd(k,n)|n\).只要选适当的k使得\(\gcd(k,n)>1\)就可以求得一个约数\(\gcd(k,n)\).这样的k数量还是蛮多的:k有若干个质因子,而每个质因子的倍数都是可行的.
我们不放选取一组数\(x_1,x_2,x_3,\dots,x_n\),若有\(gcd(|x_i-x_j|,N)>1\),则称\(gcd(|x_i-x_j|,N)\)是N的一个因子.早期的论文中有证明,需要选取的数的个数大约是\(O(N^{\frac{1}{4}})\).但是,我们还需要解决储存方面的问题.如果\(N=10^{18}\),那么我们也需要取\(10^4\)个数.如果还要\(O(n^2)\)来两两比较,时间复杂度又会弹回去.
我们不妨考虑构造一个伪随机数序列,然后取相邻的两项来求gcd.为了生成一串优秀的随机数,Pollard设计了这样一个函数:
\(f(x)=(x^2+c)\mod N\)
其中c是一个随机的常数.
我们随便取一个\(x_1\),令\(x_2=f(x_1)\),\(x_3=f(x_2)\),\(\dots\),\(x_i=f(x_{i-1})\).在一定的范围内,这个数列是基本随机的,可以取相邻两项作差求gcd.
生成随机函数的方式有很多种,比如\(\alpha_j-y\)函数.但是这个函数生成出来的伪随机数效果比较好.它的图像长这个样子:
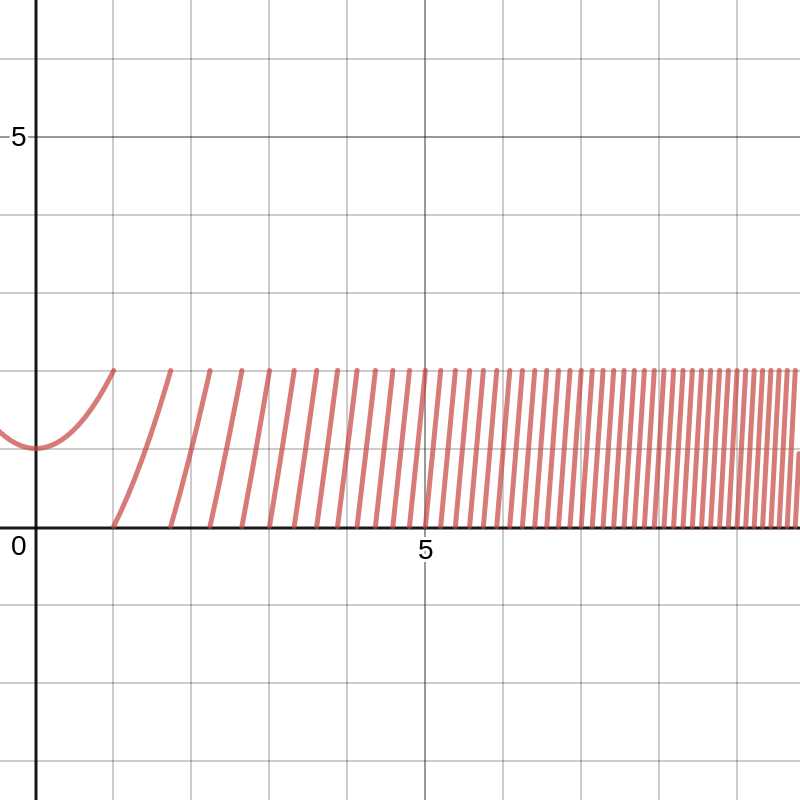
选取这个函数是自有道理的.有一种几何图形叫做曼德勃罗集,它是用\(f(x)=x^2+c\),然后带入复数,用上面讲到的方式进行迭代的.

↑曼德勃罗集.每个点的坐标代表一个复数\(x_1\),然后根据数列的发散速度对这个点染色.
这个图形和所谓的混沌系统有关.我猜大概是混沌这个性质保证了Pollard函数会生成一串优秀的伪随机数吧.
不过之所以叫伪随机数,是因为这个数列里面会包含有"死循环".
\({1,8,11,8,11,8,11,\dots}\)这个数列是\(c=7,N=20,x_1=1\)时得到的随机数列.这个数列会最终在8和11之间不断循环.循环节的产生不难理解:在模N意义下,整个函数的值域只能是\({0,1,2,\dots,N-1}\).总有一天,函数在迭代的过程中会带入之前的值,得到相同的结果.
生成数列的轨迹很像一个希腊字母\(\rho\),所以整个算法的名字叫做Pollard Rho.
为了判断环的存在,可以用一个简单的Floyd判圈算法,也就是"龟兔赛跑".
假设乌龟为\(t\),兔子为\(r\),初始时\(t=r=1\).假设兔子的速度是乌龟的一倍.
过了时间\(i\)后,\(t=i,r=2i\).此时两者得到的数列值\(x_t=x_i,x_r=x_{2i}\).
假设环的长度为\(c\),在环内恒有:\(x_i=x_{i+c}\).
如果龟兔"相遇",此时有:\(x_r=x_t\),也就是\(x_i=x_{2i}=x_{i+c}\),解得\(i=c\).(自己动笔算了之后发现,长链+自环的结构好像不符合这个公式,也不知道怎么回事)
这样以来,我们得到了一套基于Floyd判圈算法的Pollard Rho 算法.
int f(int x,int c,int n)
{
return (x*x+c)%n;
}
int pollard_rho(int N)
{
int c=rand()%(N-1)+1;
int t=f(0,c,N),r=f(f(0,c,N),c,N);//两倍速跑
while(t!=r)
{
int d=gcd(abs(t-r),N);
if(d>1)
return d;
t=f(t,c,N),r=f(f(r,c,N),c,N);
}
return N;//没有找到,重新调整参数c
}原文:https://www.cnblogs.com/LinearODE/p/10542226.html