6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。

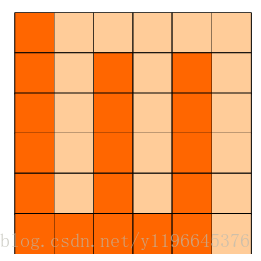
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
思路:从中间点搜索碰到边界答案就加1 然后值得注意的是每一次都要标记两个点 因为是对称搜索的 其次最后答案需要除4,因为题目中说要旋转对称的是同一种。
#include<cstdio> #include<cstring> #include<algorithm> #include<iostream> #include<string> #include<vector> #include<stack> #include<bitset> #include<cstdlib> #include<cmath> #include<set> #include<list> #include<deque> #include<map> #include<queue> #define ll long long int using namespace std; inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;} inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;} int moth[13]={0,31,28,31,30,31,30,31,31,30,31,30,31}; int dir[4][2]={1,0 ,0,1 ,-1,0 ,0,-1}; int dirs[8][2]={1,0 ,0,1 ,-1,0 ,0,-1, -1,-1 ,-1,1 ,1,-1 ,1,1}; const int inf=0x3f3f3f3f; const ll mod=1e9+7; int ans; bool vis[10][10]; void dfs(int x,int y){ if(x==0||x==6||y==0||y==6){ ans++; return ; } for(int i=0;i<4;i++){ int xx=x+dir[i][0]; int yy=y+dir[i][1]; if(xx>=0&&xx<=6&&yy>=0&&yy<=6&&!vis[xx][yy]){ vis[xx][yy]=1; vis[6-xx][6-yy]=1; dfs(xx,yy); vis[xx][yy]=0; vis[6-xx][6-yy]=0; } } } int main(){ ios::sync_with_stdio(false); ans=0; vis[3][3]=1; dfs(3,3); cout<<ans/4<<endl; return 0; }
原文:https://www.cnblogs.com/wmj6/p/10543344.html