一 无向图单源最短路径,Dijkstra算法
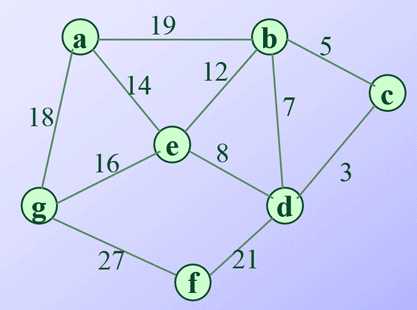
计算源点a到图中其他节点的最短距离,是一种贪心算法。利用局部最优,求解全局最优解。
设立一个visited访问和dist距离数组,在初始化后每一次收集一个当前最短的节点cur并将其标记为visited,然后更新这个节点的未被收集临近节点的dist值 [ if ( visited[t] != True && (dis[cur]+ Graph[cur][t]) < dis[t] ) ],直到所有节点被访问。查找dist中的最短路径节点,可使用最小堆或二项堆,降低时间复杂度。
二
/* Dijkstra of shortest path of single source in graph */ #include <stdio.h> #define MAX 100 /* int as +/-[2^31] --> 0-2147483647 */ #define INFIN 2147483647 enum BOOL { False, True }; int Graph[MAX][MAX]; /* matrix of graph */ int dis[MAX]; /* distance from origin other nodes */ BOOL visited[MAX]; void Dijkstra( int v0 , int N); int main(int argc, char *argv[]) { int i, j, k; int N, M, src, dst, distance; int start; /* input vertex number and edge number */ scanf("%d%d", &N, &M); /* Initialize the vertax and edge of graph matrix */ for ( i = 0; i < N; i++ ) { for ( j = 0; j < N; j++ ) { if ( i == j ) { /* edge of vertax itself*/ Graph[i][j] = 0; } else { /* all edge large than 0, unless it‘s unkonwn */ Graph[i][j] = INFIN; } } } /* Init the orignal graph edge */ printf("Please input the init edge\n"); for ( k = 0; k < M; k++ ) { scanf("%d%d%d", &src, &dst, &distance); Graph[src][dst] = distance; } printf("Please input the start vertax:"); scanf("%d", &start); if ( start >= 0 ) { Dijkstra( start, N); printf("Distance from %d to others as follows:\n", start); printf("src --> dst\n"); for ( k = 0; k < N; k++ ) { printf("%d-->%d cost:%d ", start, k, dis[k]); if ( k > 0 && (k % 3) == 0 ) { printf("\n"); } } } return 0; } void Dijkstra( int v0, int N ) { /* Init dis */ int i, j, k, t; /* cur represent current vertax */ int cur, mini_dis; for ( i = 0; i < N; i++ ) { dis[i] = Graph[v0][i]; visited[i] = False; } cur = v0; visited[v0] = True; mini_dis = INFIN; /* find dis to another MAX-1 points */ for ( j = 1; j < N; j++ ) { /* for simple use,iterate the array to find a shortest*/ for ( k = 0; k < N; k++ ) { if ( visited[k] != True && dis[k] < mini_dis ) { mini_dis = dis[k]; cur = k; } } visited[cur] = True; /* Update the correlated dis with current shortest point */ for ( t = 0; t < N; t++ ) { if ( Graph[cur][t] < dis[t] ) { /* update if dis to [cur veratx + edge] < [dis to t] */ if ( visited[t] != True && (dis[cur]+ Graph[cur][t]) < dis[t] ) { dis[t] = dis[cur] + Graph[cur][t]; } } } } }
原文:https://www.cnblogs.com/justLittleStar/p/10544141.html