Siruseri 城中的道路都是单向的。不同的道路由路口连接。按照法律的规定， 在每个路口都设立了一个 Siruseri 银行的 ATM 取款机。令人奇怪的是，Siruseri 的酒吧也都设在路口，虽然并不是每个路口都设有酒吧。
Banditji 计划实施 Siruseri 有史以来最惊天动地的 ATM 抢劫。他将从市中心 出发，沿着单向道路行驶，抢劫所有他途径的 ATM 机，最终他将在一个酒吧庆 祝他的胜利。
使用高超的黑客技术，他获知了每个 ATM 机中可以掠取的现金数额。他希 望你帮助他计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可 以经过同一路口或道路任意多次。但只要他抢劫过某个 ATM 机后，该 ATM 机 里面就不会再有钱了。 例如，假设该城中有 6 个路口，道路的连接情况如下图所示：
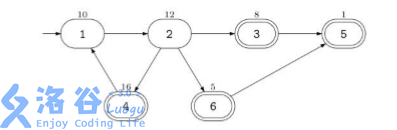
市中心在路口 1，由一个入口符号→来标识，那些有酒吧的路口用双圈来表
示。每个 ATM 机中可取的钱数标在了路口的上方。在这个例子中，Banditji 能抢 劫的现金总数为 47，实施的抢劫路线是：1-2-4-1-2-3-5。
输入格式：
第一行包含两个整数 N、M。N 表示路口的个数，M 表示道路条数。接下来 M 行，每行两个整数，这两个整数都在 1 到 N 之间，第 i+1 行的两个整数表示第 i 条道路的起点和终点的路口编号。接下来 N 行，每行一个整数，按顺序表示每 个路口处的 ATM 机中的钱数。接下来一行包含两个整数 S、P，S 表示市中心的 编号，也就是出发的路口。P 表示酒吧数目。接下来的一行中有 P 个整数，表示 P 个有酒吧的路口的编号。
输出格式：
输出一个整数，表示 Banditji 从市中心开始到某个酒吧结束所能抢劫的最多 的现金总数。
50%的输入保证 N, M<=3000。所有的输入保证 N, M<=500000。每个 ATM 机中可取的钱数为一个非负整数且不超过 4000。
输入数据保证你可以从市中心 沿着 Siruseri 的单向的道路到达其中的至少一个酒吧。
这道题给我最大的帮助就是，终于找到了我手动模拟堆栈时候会出现的一个问题。
终于解决了为什么开st的栈就AC，而手模就死的问题。
这个小问题只要是我们这样不背模板的人都可能会犯的，一会会细致的介绍（你可能也是WA在这里了QAQ）
先讲一下思路。
作为一道典型的缩点题，这题强连通的暗示也太强了吧。
在有向图里，可以绕来绕去的情况下，取尽可能大的值。然后要求在有酒吧的点里尽可能大。
那么我们来看一张图。
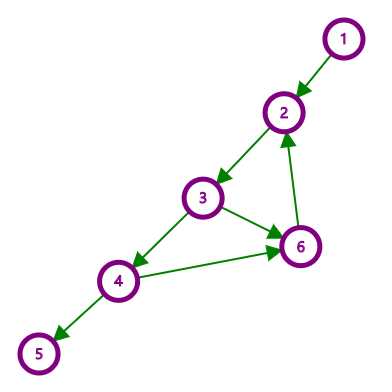（原创！！）
在这张图中我们可以很容易的发现{1}，{2.3.4.6}，{5}是三个强连通分量。
所以我们就可以想到这题的第一种写法：
这就只有一个要注意的地方：是将团体连边，不是让点于点之间连边哦~。
放上代码》特别感谢代码原主人！！
1 #include <cstdio> 2 int f[2000001],chu[2000001],bb[2000001],l[2000001]; 3 struct nodea{ int h,i,b,v,d; } a[5000001]; 4 struct nodeb{ int x,y,gg; } b[5000001]; 5 int len=0,tou=0,lx=0,lb=0,n=0,m=0,st=0,p=0; 6 void ins(int x,int y) 7 { 8 len++; 9 b[len].x=x; 10 b[len].y=y; 11 b[len].gg=a[x].h; 12 a[x].h=len; 13 } 14 void dfs(int x) 15 { 16 l[++tou]=x; 17 a[x].i=++lx; 18 a[x].d=lx; 19 a[x].v=1; 20 for(int i=a[x].h;i>0;i=b[i].gg) 21 { 22 int y=b[i].y; 23 if(a[y].i==0) 24 { 25 dfs(y); 26 if(a[y].d<a[x].d) 27 { 28 a[x].d=a[y].d; 29 } 30 } 31 else if(a[y].v==1) 32 { 33 if(a[y].i<a[x].d) 34 { 35 a[x].d=a[y].i; 36 } 37 } 38 } 39 if(a[x].i==a[x].d) 40 { 41 lb++; 42 while(true) 43 { 44 int k=l[tou--]; 45 a[k].v=0; 46 a[k].b=lb; 47 if(k==x) 48 { 49 break; 50 } 51 } 52 } 53 } 54 void spfa() 55 { 56 int tou=1,wei=2; 57 f[1]=st; 58 a[st].v=1; 59 a[st].d=bb[st]; 60 while(tou!=wei) 61 { 62 int x=f[tou]; 63 for(int i=a[x].h;i>0;i=b[i].gg) 64 { 65 int y=b[i].y; 66 if(a[y].d<a[x].d+bb[y]) 67 { 68 a[y].d=a[x].d+bb[y]; 69 if(a[y].v==0) 70 { 71 a[y].v=1; 72 f[wei]=y; 73 wei++; 74 if(wei>lb) 75 { 76 wei=1; 77 } 78 } 79 } 80 } 81 a[x].v=0; 82 tou++; 83 if(tou>lb) 84 { 85 tou=1; 86 } 87 } 88 } 89 int main() 90 { 91 scanf("%d %d",&n,&m); 92 for(int i=1;i<=m;i++) 93 { 94 int x=0,y=0; 95 scanf("%d %d",&x,&y); 96 ins(x,y); 97 } 98 for(int i=1;i<=n;i++) 99 { 100 if(a[i].i==0) 101 { 102 dfs(i); 103 } 104 } 105 int td=0; 106 for(int i=1;i<=n;i++) 107 { 108 a[i].h=0; 109 a[i].v=0; 110 a[i].d=0; 111 scanf("%d",&td); 112 bb[a[i].b]+=td; 113 } 114 scanf("%d %d",&st,&p); 115 int now=len; 116 len=0; 117 for(int i=1;i<=now;i++) 118 { 119 int x=b[i].x; 120 int y=b[i].y; 121 if(a[x].b!=a[y].b) 122 { 123 ins(a[x].b,a[y].b); 124 } 125 } 126 st=a[st].b; 127 spfa(); 128 int ans=0; 129 int tx=0; 130 for(int i=1;i<=p;i++) 131 { 132 scanf("%d",&tx); 133 if(ans<a[a[tx].b].d) 134 { 135 ans=a[a[tx].b].d; 136 } 137 } 138 printf("%d",ans); 139 return 0; 140 }
一看就不是我的风格QAQ
那么这题就完成了？
想的美！
接下来介绍我的写法。
很显然这缩点后的图是一个DAG
DAG上搞DP这不是基本操作吗？？？那我们就按拓扑序搞一波DP就好了啊！！
假设 f[ i ] 表示从起点抢劫到 DAG 上的点 i 时能得到的最多的钱
那么就有了：
f[ i ] = max( f [ i ] , f[ j ] + mon i ]) （ j 有一条边指向 i , smon i ] 表示DAG上点 i 的钱数）
至于 Tarjan 的具体操作我之前有讲到，自觉讲的很详细了，这里不再赘述
测了一波，自己的DP比SPFA快个100ms（都开了O2）
放上代码
#include<iostream> #include<cstring> #include<cstdio> #include<cmath> #include<algorithm> #include<queue> using namespace std; const int MA=5e5+7; int n,m,k,str,ans; int head[MA],ecnt,Head[MA],Ecnt,c[MA]; int val[MA],du[MA],f[MA]; int dfn[MA],low[MA],st[MA],be[MA],dis[MA]; int num,ti,tp; bool bar[MA],Bar[MA]; struct ss{ int to,nxt; }t[MA],d[MA]; queue<int> q; inline int read() { int x=0;char ch=getchar(); while(ch<‘0‘||ch>‘9‘)ch=getchar(); while(ch>=‘0‘&&ch<=‘9‘)x=(x<<3)+(x<<1)+ch-‘0‘,ch=getchar(); return x; } inline void add(int a,int b) { t[++ecnt].to=head[a]; t[ecnt].nxt=b; head[a]=ecnt; return; } inline void add2(int a,int b) { d[++Ecnt].to=Head[a]; d[Ecnt].nxt=b; Head[a]=Ecnt; return; } void Tar(int x) { dfn[x]=low[x]=++ti; be[x]=1; st[++tp]=x; for(int i=head[x];i;i=t[i].to) { int v=t[i].nxt; if(!dfn[v]) { Tar(v); low[x]=min(low[x],low[v]); } else if(be[v]) low[x]=min(low[x],dfn[v]); } if(dfn[x]==low[x]) { ++num; while(st[tp]!=x) { c[st[tp]]=num; dis[num]+=val[st[tp]]; be[st[tp]]=0; if(bar[st[tp]]) Bar[num]=1; tp--;
//没错就是这个地方坑我！！
// 我们在这个地方应该是先更改top的性质和值再进行tp--操作！！
//其实只有我错了对不对，我是脑残QAQ
} if(bar[st[tp]]) Bar[num]=1; dis[num]+=val[st[tp]]; c[st[tp]]=num; be[st[tp--]]=0; } } void build() { for(int i=1;i<=n;i++) { if(!dfn[i]) continue; for(int j=head[i];j;j=t[j].to) { int v=t[j].nxt; if(!dfn[v]) continue; if(c[i]==c[v]) continue; add2(c[i],c[v]); du[c[v]]++; } } return; } void DP() { q.push(c[str]); f[c[str]]=dis[c[str]]; while(!q.empty()) { int u=q.front(); q.pop(); for(int i=Head[u];i;i=d[i].to){ int v=d[i].nxt; f[v]=max(f[v],f[u]+dis[v]); if(!(--du[v])) q.push(v); } } return; } int main() { n=read(); m=read(); for(int i=1;i<=m;i++) { int a=read(); int b=read(); add(a,b); } for(int i=1;i<=n;i++) val[i]=read(); str=read(); k=read(); for(int i=1;i<=k;i++) { int a=read(); bar[a]=1; } Tar(str); build(); DP(); for(int i=1;i<=n;i++) if(bar[i]) ans=max(ans,f[c[i]]); printf("%d\n",ans); return 0; }
这样就完成了。
谢谢！
原文：https://www.cnblogs.com/qxyzili--24/p/10551784.html