前段时间我受极视角邀请,在斗鱼上直播分享有关GAN的话题。考虑到现在网上关于GAN的文章、视频都已经非常多了,所以我就故意选择了一个之前没有什么人讲过的主题:LSTM之父Schmidhuber与GAN之间的恩怨纠葛。其实这件事在英文网上传播得还挺广,而且除了八卦之外也有一些严肃的学术讨论,可惜相关的中文信息寥寥,不过这样倒正好给我一个机会来给大家介绍一些新内容。
其实相比视频直播我还是更喜欢写成文章的形式,因为后者更适合深入理解和收藏回顾。所以为了方便错过直播或者不习惯看视频的朋友,我对当晚直播内容进行了文字整理,全文分为以下四个部分:
如果选择看直播回放,可以到百度云下载。
链接:http://pan.baidu.com/s/1skUZidn
密码:200j
2016年12月,NIPS大会,Ian Goodfellow的GAN Tutorial上,发生了尴尬的一幕。

正当Goodfellow讲到GAN与其他模型的比较时,台下一位神秘人物站起来打断了演讲,自顾自地说了一大通话(视频片段在此)


只见他站起来之后,先讲自己在1992年提出了一个叫做Predictability Minimization的模型,它如何如何,一个网络干嘛另一个网络干嘛,花了好几分钟,接着话锋一转,直问台上的Goodfellow:“你觉得我这个PM模型跟你的GAN有没有什么相似之处啊?”



回到正题,当时Schmidhuber在评审意见中认为,他92年提出的PM模型才是“第一个对抗网络”,而GAN跟PM的主要差别仅仅在于方向反过来了,可以把GAN名字改成“inverse PM”,即反过来的PM。按他的意思,GAN简直就是个PM的变种模型罢了。

Goodfellow也不客气,干脆在2016年的GAN Tutorial中完全移除了对PM的比较和引用。他在Quora上公开表示,“我从没有否认GAN跟另外一些模型有联系,比如NCE,但是GAN跟PM之间我真的认为没太大联系。”更有意思的是,Goodfellow还透露说,“Jürgen和我准备合写一篇paper来比较PM和GAN——如果我们能够取得一致意见的话。”想必真要写出来,背后又要经过一番激烈的争论了。
说了这么多,所谓的PM模型究竟是什么?它跟GAN究竟有多少相同多少不同?还有,这个“古老”的模型能给今天的GAN研究带来什么启发吗?大家心里肯定充满了疑问。那么八卦结束,我们现在就来走近科学,走近尘封多年的PM模型。
Predictability Minimization(可预测性最小化)模型,简称PM模型,出自1992年的论文《Learning Factorial Codes by Predictability Minimization》,Jürgen Schmidhuber是唯一的作者。对于类似我这样二零一几年才接触深度学习的人来说,它几乎就是“中古时期”的文献了。

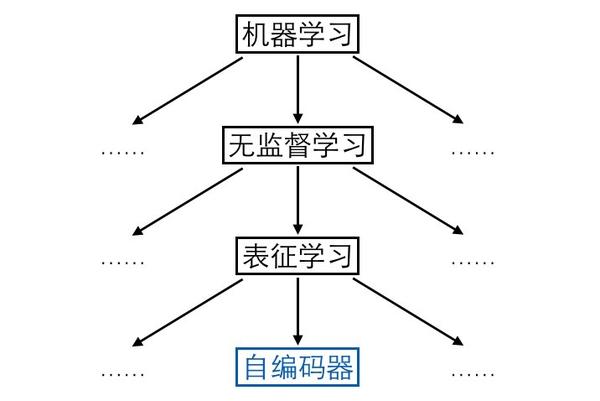
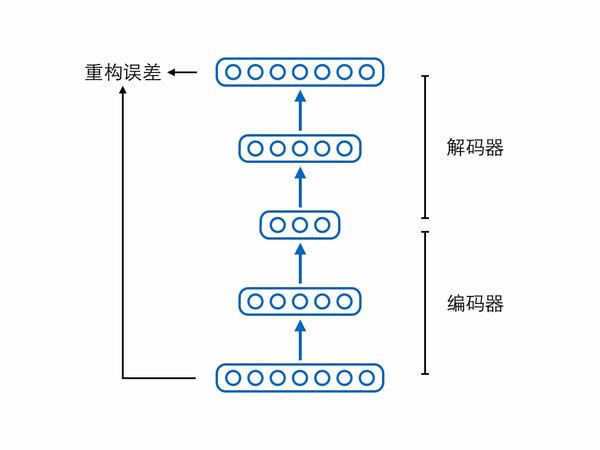
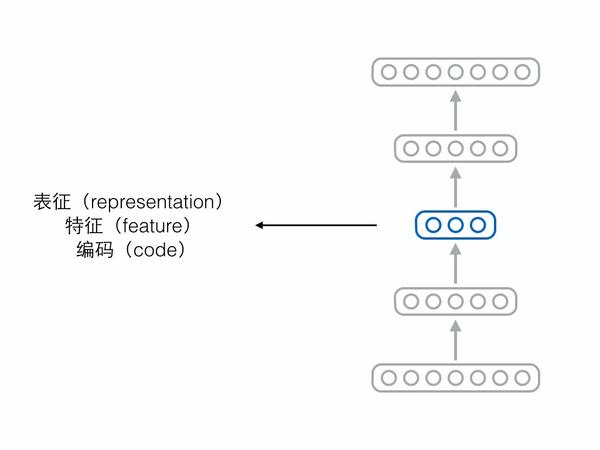
比如有人认为编码向量的各个维度代表了样本所具有的属性,而单独一个样本不应该同时具备那么多种属性,所以合理的情况是编码向量中大多数维度都是0(不激活),只有少数维度不为0(激活),此为“稀疏”,附带稀疏要求的编码器就叫稀疏自编码器。
再比如有人认为自编码器不能死记硬背,需要在“理解”样本的基础上对样本进行编码,即便输入的时候存在一些噪声损坏了样本,自编码器也要能够还原出完好的原始样本,在此条件下编码出来的向量可能会更具语义信息,此为“降噪”,附带降噪要求的编码器就叫降噪自编码器。
除了稀疏、降噪,还有人认为编码向量的各个维度之间应该相互独立,此为“解耦”(factorial / disentangled),也是下文的重点。为了方便起见,我们考虑编码只有3个维度的情况,此时解耦在数学形式上表现为:
(1)
其中是全部训练样本而非单个样本,
对应编码的第
个维度。为方便起见,下文省略
。

现在问题来了,我们可以通过L1正则化给来自编码器提出稀疏的要求,可以通过输入加噪来给自编码器提出降噪的要求,那要怎么给自编码器提出解耦的要求呢?当年Schmidhuber就想到了非常聪明的方法。
首先,上面公式(1)可以换一个表述,改写成三个条件独立表达式:
(2a)
(2b)
(2c)
直观上可以把这组式子解释为,一个编码维度旁边的“兄弟维度”对于预测该维度没有额外帮助,比如说知道了和
并不能帮助我们将
猜得更准。
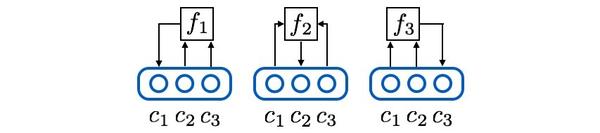
接着,使用三个预测器网络把上述逻辑具体化,其中预测器1负责预测维度1,输入维度2和3,以此类推,数学形式如下:
(3a)
(3b)
(4a)
(4b)
(4c)
按Schmidhuber的思想,上述loss体现了各个编码维度的解耦程度。怎么说呢?以预测器1为例,如果和
很有关系,甚至极端情况下
恒等于
,那么
就能够猜得很准。此时
关于
条件不独立,很有可预测性(predictability),我们就认为
没能从
中解耦。
这显然不是想要的局面。为了将与
解耦,编码器就得尽可能让预测器猜不中,loss上体现为:
(5)
预测器1想要猜中维度1,而编码器想要让它猜不中,loss函数刚好相反,,两者之间存在对抗。如果编码器赢了,就代表与
关系不大,成功解耦。
接下来考虑上所有维度,再把公式写得通用一点。每个预测器试图猜中它所负责的编码维度,体现了编码的可预测性,其loss为:
(6)
编码器试图让所有预测器都猜不中,试图最小化可预测性,其loss与预测器相反:
(7)
如果编码器赢了,就解耦了编码向量的各个维度。至此,读者就可以理解Schmidhuber论文标题的含义了:Learning Factorial Codes by Predictability Minimization,通过最小化可预测性,来学习一个解耦的编码表示。
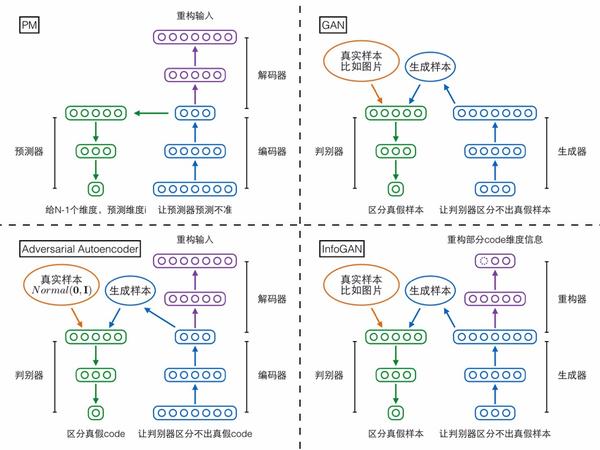
当然,除了上述两个相互对抗可预测性loss,别忘了还有个自编码器本身的重构误差loss,它能够保证编码中尽可能保留了原始输入样本的重要信息。论文中其实还有其他loss,但不是重点,感兴趣的人可以去读原论文。将上述网络模块与loss函数全部集中在一起,就形成了PM模型的总体架构图,我们用这张图作为第二部分的总结:
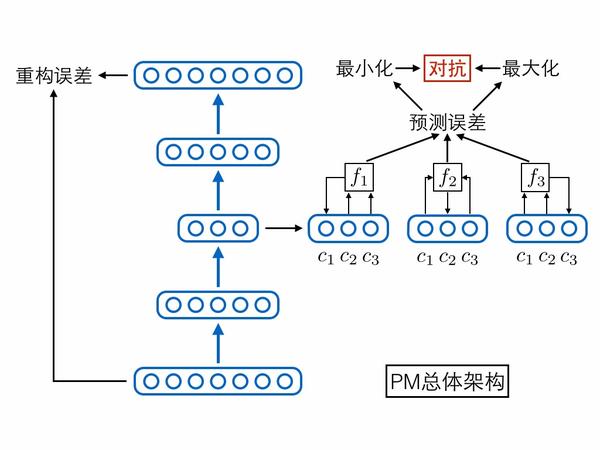
知道了PM是啥,接下来的问题就是它跟GAN究竟有多相似,但实际上GAN的两个后续变种——InfoGAN、对抗自编码器反而跟PM更像,所以第三部分先简单介绍这三个模型,再在第四部分跟PM进行综合比较。相关论文如下:
Generative Adversarial Nets第一个模型是大家已经很熟悉的GAN,分为生成器(generator)和判别器(discriminator)两个模块。生成器输入一个随机编码向量,输出一个复杂样本(如图片);判别器输入一个复杂样本,输出一个概率表示该样本是真实样本还是生成器产生的假样本。判别器的目标是区分真假样本,生成器的目标是让判别器区分不出真假样本,两者目标相反,存在对抗。
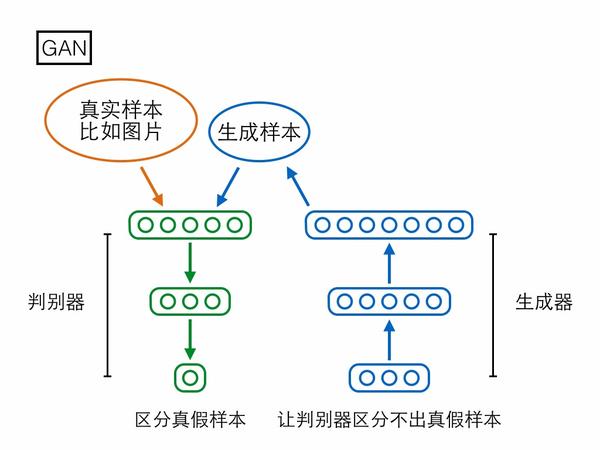
第二个模型InfoGAN却可以做到。先来看它的结构,相比GAN多了个重构器模块,用于重构生成器输入的随机编码向量,但是只重构由我们指定的一部分维度。
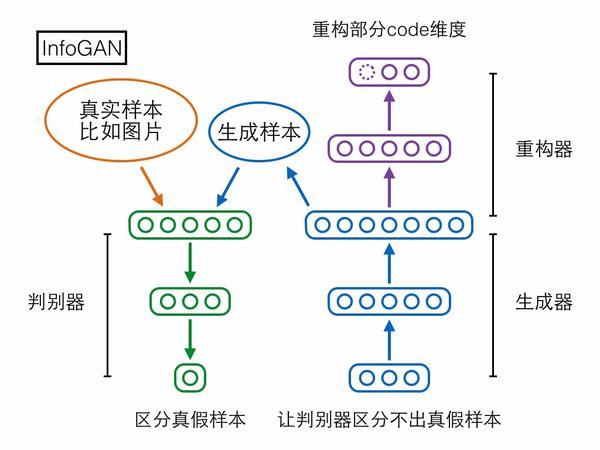

无论是GAN、InfoGAN还是其他GAN变种,基本上都想学习从零均值、一方差的标准高斯分布到复杂样本分布的映射,而GAN的思路是先固定前者(标准高斯分布)作为网络输入,再慢慢调整网络输出去匹配后者(复杂样本分布)。
第三个模型Adversarial Autoencoder(对抗自编码器)却采取了相反的思路!它是先固定后者(复杂样本分布)作为网络输入,再慢慢调整网络输出去匹配前者(标准高斯分布)。具体来说,对抗自编码器包含三个模块——编码器、解码器、判别器,前两者构成一个普通的自编码器,输入的复杂样本,还是要求在解码器的输出端重构;判别器输入编码向量,判定它是来自一个真实的标准高斯分布,还是来自编码器的输出。判别器试图区分编码向量的真假,编码器就试图让判别器区分不出真假,如果最终编码器赢了,就意味着它输出的编码很接近标准高斯分布,导致判别器混淆不清,我们的目的也就达到了。对抗自编码器严格来说应该不算GAN的变种,因为它的思路方向与GAN相反。
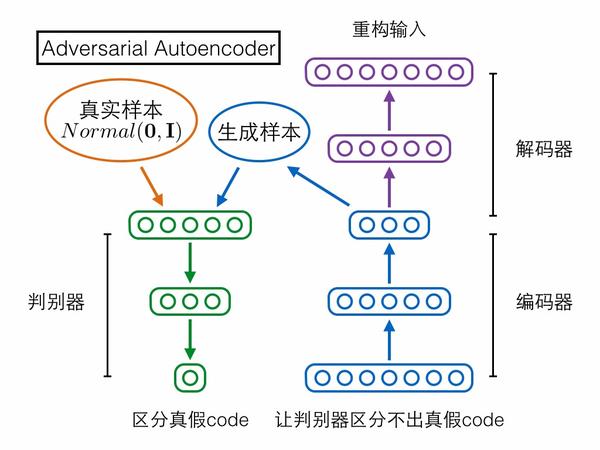
需要注意的是,上图其实把N个预测器合并画成了一个。
最后,一图总结第三部分:
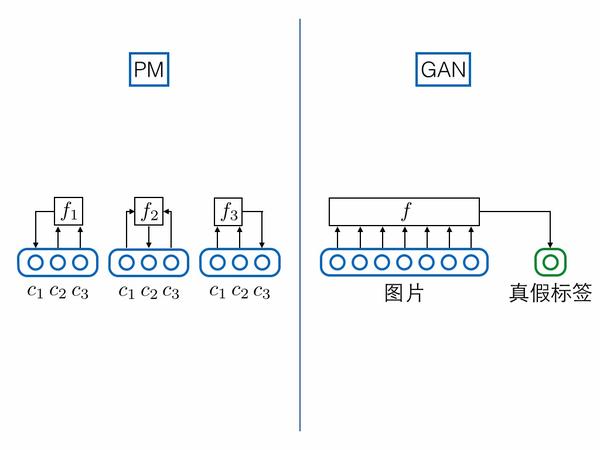
最后是对上述四个模型做综合比较。首先对比PM和GAN:
1.映射方向相反
其中PM的编码器和GAN的生成器方向相反,所以Schmidhuber把GAN称为“inverse PM”。
2.都是对抗优化相反的目标
3.预测/判别结构相似
如果把真假标签的节点跟图片样本节点拼接到一起,视为一个超长向量的话,GAN的判别器就可以强行视为PM预测器的特例:PM对每一个维度都要预测,但是GAN只预测真假标签这一特殊维度。
5.可拓展性不同
Goodfellow在GAN论文中还提了其他不同点,但是我个人觉得不合理,就忽略不讲了。经过上述比较,我们可以看到PM和GAN确实有非常多的相似之处,但是差异也很大,我个人觉得并不能把GAN简单看作PM的变种。
相比之下,PM和InfoGAN、对抗自编码器反倒更像:
1.模型主体
2.对网络中间层的要求
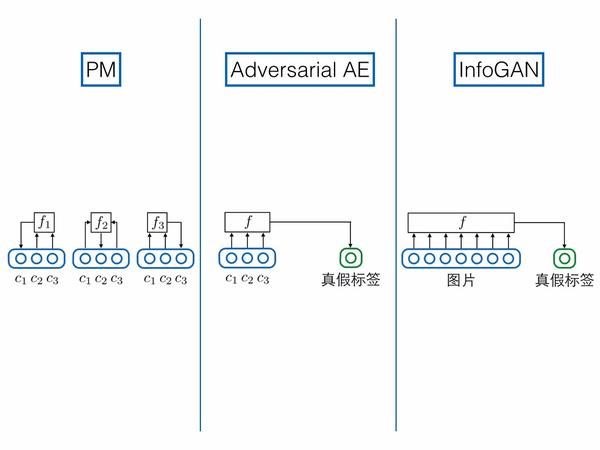
3.预测/判别结构相似
PM输入编码其他维度,预测某一维度;对抗自编码器,输入编码全部维度,预测真假标签;InfoGAN和前面GAN的情况相同,输入图片,预测真假标签。在这个角度上对抗自编码器与PM更相似。
inference.vc是一个关于生成模型的著名博客,其中有篇文章认为对抗自编码器中用GAN来拉近编码分布和高斯分布,是杀鸡用牛刀的做法。

看了PM之后就可以想到另一个思路——分别要求解耦和高斯。先把对抗自编码器的判别器换成PM模型的N组预测器,用可预测性最小化的思想,实现编码向量各个维度之间的解耦;接着对每个单独的编码维度,通过GAN使其满足高斯分布。虽然还是用GAN,但是我们把向量上的对抗训练转化为标量上的对抗训练,而后者可能比前者要容易和稳定得多。
Schmidhuber在92年提出的PM模型通过可预测性最小化来学习一个解耦的编码表示,编码器和预测器优化相反的目标,确实是比GAN更早地使用了对抗训练的思想。
PM不仅跟GAN,还跟InfoGAN、对抗自编码器存在很多相似之处,但还是有很明显的差异。其中PM和对抗自编码器最像,主体都是自编码器,但它们并不能简单地视为GAN的变种。
我们现在都是盯着最新最前沿的研究工作,其实也许有很多像PM这样“古老”但有趣的想法被我们忽视了,有的是因为当年提出的时候思想太过超前,或者硬件计算能力撑不起来,导致无人问津,最典型的例子就是LSTM。这些工作不应该被埋没,如果能够重新挖掘出来的话,就可能给今天的研究带来很多新的启发。
原文:https://www.cnblogs.com/jiangkejie/p/10581133.html