这个主要是线性回归和逻辑回归部分,除了前面关于最小二乘法,后面基本都看不懂,只做了记录。
二维线性模型:普通最小二乘法:


1 from __future__ import print_function 2 import numpy as np 3 import matplotlib.pyplot as plt 4 from scipy.optimize import minimize 5 6 # For reproducibility 7 np.random.seed(1000) 8 # Number of samples 9 nb_samples = 200 10 11 def loss(v): 12 e = 0.0 13 for i in range(nb_samples): 14 e += np.square(v[0] + v[1]*X[i] - Y[i]) 15 return 0.5 * e 16 17 def gradient(v): 18 g = np.zeros(shape=2) 19 for i in range(nb_samples): 20 g[0] += (v[0] + v[1]*X[i] - Y[i]) 21 g[1] += ((v[0] + v[1]*X[i] - Y[i]) * X[i]) 22 return g 23 24 def show_dataset(X, Y): 25 fig, ax = plt.subplots(1, 1, figsize=(5, 5)) 26 ax.scatter(X, Y) 27 ax.set_xlabel(‘X‘) 28 ax.set_ylabel(‘Y‘) 29 ax.grid() 30 plt.show() 31 32 if __name__ == ‘__main__‘: 33 # Create dataset 34 X = np.arange(-5, 5, 0.05) 35 Y = X + 2 36 Y += np.random.uniform(-0.5, 0.5, size=nb_samples) 37 38 # Show the dataset 39 show_dataset(X, Y) 40 41 # Minimize loss function 42 result = minimize(fun=loss, x0=np.array([0.0, 0.0]), jac=gradient, method=‘L-BFGS-B‘) 43 44 print(‘Interpolating rect:‘) 45 print(‘y = %.2fx + %2.f‘ % (result.x[1], result.x[0])) 46 47 # Compute the absolute error 48 err = 0.0 49 50 for i in range(nb_samples): 51 err += np.abs(Y[i] - (result.x[1]*X[i] + result.x[0])) 52 53 print(‘Absolute error: %.2f‘ % err)
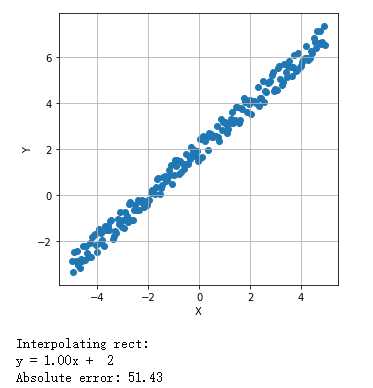
基于scikit-learn的线性回归和更高维:
利用k折交叉验证完成测试:
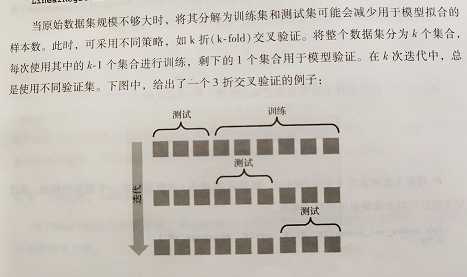
在交叉验证中,使用scoring=‘r2‘时,R2接近于1效果好,接近0模型差。R2=1-(xxx/XXXXX)

1 from __future__ import print_function 2 import numpy as np 3 import matplotlib.pyplot as plt 4 from sklearn.datasets import load_boston 5 from sklearn.linear_model import LinearRegression 6 from sklearn.model_selection import train_test_split, cross_val_score 7 # For reproducibility 8 np.random.seed(1000) 9 def show_dataset(data): 10 fig, ax = plt.subplots(4, 3, figsize=(20, 15)) 11 for i in range(4): 12 for j in range(3): 13 ax[i, j].plot(data.data[:, i + (j + 1) * 3]) 14 ax[i, j].grid() 15 plt.show() 16 17 if __name__ == ‘__main__‘: 18 # Load dataset 19 boston = load_boston() 20 # Show dataset 21 show_dataset(boston) 22 # Create a linear regressor instance 23 lr = LinearRegression(normalize=True) 24 # Split dataset 25 X_train, X_test, Y_train, Y_test = train_test_split(boston.data, boston.target, test_size=0.1) 26 # Train the model 27 lr.fit(X_train, Y_train) 28 print(‘Score %.3f‘ % lr.score(X_test, Y_test)) 29 # CV score k折交叉验证,负均方差验证 30 scores = cross_val_score(lr, boston.data, boston.target, cv=7, scoring=‘neg_mean_squared_error‘) 31 print(‘CV Negative mean squared errors mean: %.3f‘ % scores.mean()) 32 print(‘CV Negative mean squared errors std: %.3f‘ % scores.std()) 33 # CV R2 score k折交叉验证,决定系数验证 34 r2_scores = cross_val_score(lr, boston.data, boston.target, cv=10, scoring=‘r2‘) 35 print(‘CV R2 score: %.3f‘ % r2_scores.mean())

求得的回归表达式和结果:(不理想的结果)

1 print(‘y=‘+ str(lr.intercept_)+‘ ‘) 2 for i,c in enumerate(lr.coef_): 3 print(str(c)+‘*x‘+str(i)) 4 X = boston.data[0:10]+np.random.normal(0.0,0.1) 5 lr.predict(X)
boston.target[0:10]

Ridge、Lasso、ElasticNet回归:

1 from __future__ import print_function 2 import numpy as np 3 from sklearn.datasets import load_diabetes 4 from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet, RidgeCV, LassoCV, ElasticNetCV 5 from sklearn.model_selection import cross_val_score 6 # For reproducibility 7 np.random.seed(1000) 8 if __name__ == ‘__main__‘: 9 diabetes = load_diabetes() 10 # Create a linear regressor and compute CV score 11 lr = LinearRegression(normalize=True) 12 lr_scores = cross_val_score(lr, diabetes.data, diabetes.target, cv=10) 13 print(‘Linear regression CV score: %.6f‘ % lr_scores.mean()) 14 # Create a Ridge regressor and compute CV score 15 rg = Ridge(0.005, normalize=True) 16 rg_scores = cross_val_score(rg, diabetes.data, diabetes.target, cv=10) 17 print(‘Ridge regression CV score: %.6f‘ % rg_scores.mean()) 18 # Create a Lasso regressor and compute CV score 19 ls = Lasso(0.01, normalize=True) 20 ls_scores = cross_val_score(ls, diabetes.data, diabetes.target, cv=10) 21 print(‘Lasso regression CV score: %.6f‘ % ls_scores.mean()) 22 # Create ElasticNet regressor and compute CV score 23 en = ElasticNet(alpha=0.001, l1_ratio=0.8, normalize=True) 24 en_scores = cross_val_score(en, diabetes.data, diabetes.target, cv=10) 25 print(‘ElasticNet regression CV score: %.6f‘ % en_scores.mean()) 26 27 # Find the optimal alpha value for Ridge regression 28 rgcv = RidgeCV(alphas=(1.0, 0.1, 0.01, 0.001, 0.005, 0.0025, 0.001, 0.00025), normalize=True) 29 rgcv.fit(diabetes.data, diabetes.target) 30 print(‘Ridge optimal alpha: %.3f‘ % rgcv.alpha_) 31 # Find the optimal alpha value for Lasso regression 32 lscv = LassoCV(alphas=(1.0, 0.1, 0.01, 0.001, 0.005, 0.0025, 0.001, 0.00025), normalize=True) 33 lscv.fit(diabetes.data, diabetes.target) 34 print(‘Lasso optimal alpha: %.3f‘ % lscv.alpha_) 35 # Find the optimal alpha and l1_ratio for Elastic Net 36 encv = ElasticNetCV(alphas=(0.1, 0.01, 0.005, 0.0025, 0.001), l1_ratio=(0.1, 0.25, 0.5, 0.75, 0.8), normalize=True) 37 encv.fit(diabetes.data, diabetes.target) 38 print(‘ElasticNet optimal alpha: %.3f and L1 ratio: %.4f‘ % (encv.alpha_, encv.l1_ratio_))

随机采样一致的鲁棒回归:

1 from __future__ import print_function 2 import numpy as np 3 import matplotlib.pyplot as plt 4 from sklearn.linear_model import LinearRegression, RANSACRegressor 5 # For reproducibility 6 np.random.seed(1000) 7 nb_samples = 200 8 nb_noise_samples = 150 9 10 def show_dataset(X, Y): 11 fig, ax = plt.subplots(1, 1, figsize=(10, 8)) 12 ax.scatter(X, Y) 13 ax.set_xlabel(‘X‘) 14 ax.set_ylabel(‘Y‘) 15 ax.grid() 16 plt.show() 17 18 if __name__ == ‘__main__‘: 19 # Create dataset 20 X = np.arange(-5, 5, 0.05) 21 Y = X + 2 22 Y += np.random.uniform(-0.5, 0.5, size=nb_samples) 23 for i in range(nb_noise_samples, nb_samples): 24 Y[i] += np.random.uniform(12, 15) 25 # Show the dataset 26 show_dataset(X, Y) 27 # Create a linear regressor 28 lr = LinearRegression(normalize=True) 29 lr.fit(X.reshape(-1, 1), Y.reshape(-1, 1)) 30 print(‘Standard regressor: y = %.3fx + %.3f‘ % (lr.coef_, lr.intercept_)) 31 # Create RANSAC regressor 32 rs = RANSACRegressor(lr) 33 rs.fit(X.reshape(-1, 1), Y.reshape(-1, 1)) 34 print(‘RANSAC regressor: y = %.3fx + %.3f‘ % (rs.estimator_.coef_, rs.estimator_.intercept_))
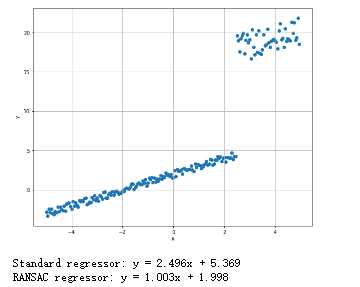
多项式回归:

1 from __future__ import print_function 2 import numpy as np 3 import matplotlib.pyplot as plt 4 from sklearn.linear_model import LinearRegression 5 from sklearn.model_selection import train_test_split 6 from sklearn.preprocessing import PolynomialFeatures 7 # For reproducibility 8 np.random.seed(1000) 9 nb_samples = 200 10 def show_dataset(X, Y): 11 fig, ax = plt.subplots(1, 1, figsize=(10, 8)) 12 ax.scatter(X, Y) 13 ax.set_xlabel(‘X‘) 14 ax.set_ylabel(‘Y‘) 15 ax.grid() 16 plt.show() 17 18 if __name__ == ‘__main__‘: 19 # Create dataset 20 X = np.arange(-5, 5, 0.05) 21 Y = X + 2 22 Y += X**2 + np.random.uniform(-0.5, 0.5, size=nb_samples) 23 # Show the dataset 24 show_dataset(X, Y) 25 # Split dataset 26 X_train, X_test, Y_train, Y_test = train_test_split(X.reshape(-1, 1), Y.reshape(-1, 1), test_size=0.25) 27 lr = LinearRegression(normalize=True) 28 lr.fit(X_train, Y_train) 29 print(‘Linear regression score: %.3f‘ % lr.score(X_train, Y_train)) 30 # Create polynomial features 31 pf = PolynomialFeatures(degree=2) 32 X_train = pf.fit_transform(X_train) 33 X_test = pf.fit_transform(X_test) 34 lr.fit(X_train, Y_train) 35 print(‘Second degree polynomial regression score: %.3f‘ % lr.score(X_train, Y_train))
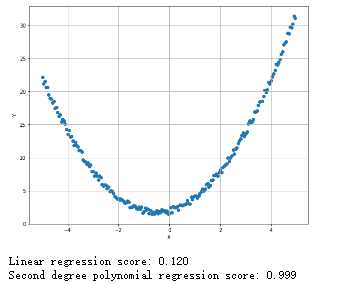
保序回归:

1 from __future__ import print_function 2 import numpy as np 3 import matplotlib.pyplot as plt 4 from matplotlib.collections import LineCollection 5 from sklearn.isotonic import IsotonicRegression 6 # For reproducibility 7 np.random.seed(1000) 8 nb_samples = 100 9 def show_dataset(X, Y): 10 fig, ax = plt.subplots(1, 1, figsize=(10, 8)) 11 ax.plot(X, Y, ‘b.-‘) 12 ax.grid() 13 ax.set_xlabel(‘X‘) 14 ax.set_ylabel(‘Y‘) 15 plt.show() 16 17 def show_isotonic_regression_segments(X, Y, Yi, segments): 18 lc = LineCollection(segments, zorder=0) 19 lc.set_array(np.ones(len(Y))) 20 lc.set_linewidths(0.5 * np.ones(nb_samples)) 21 fig, ax = plt.subplots(1, 1, figsize=(10, 8)) 22 ax.plot(X, Y, ‘b.‘, markersize=8) 23 ax.plot(X, Yi, ‘g.-‘, markersize=8) 24 ax.grid() 25 ax.set_xlabel(‘X‘) 26 ax.set_ylabel(‘Y‘) 27 plt.show() 28 29 if __name__ == ‘__main__‘: 30 # Create dataset 31 X = np.arange(-5, 5, 0.1) 32 Y = X + np.random.uniform(-0.5, 1, size=X.shape) 33 # Show original dataset 34 show_dataset(X, Y) 35 # Create an isotonic regressor 36 ir = IsotonicRegression(-6, 10) 37 Yi = ir.fit_transform(X, Y) 38 # Create a segment list 39 segments = [[[i, Y[i]], [i, Yi[i]]] for i in range(nb_samples)] 40 # Show isotonic interpolation 41 show_isotonic_regression_segments(X, Y, Yi, segments)
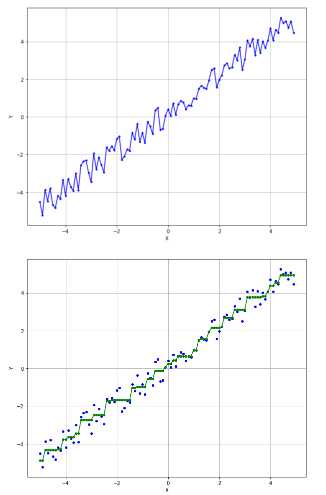
逻辑回归:

1 from __future__ import print_function 2 import numpy as np 3 import matplotlib.pyplot as plt 4 from sklearn.datasets import make_classification 5 from sklearn.model_selection import train_test_split, cross_val_score 6 from sklearn.linear_model import LogisticRegression 7 # For reproducibility 8 np.random.seed(1000) 9 nb_samples = 500 10 11 def show_dataset(X, Y): 12 fig, ax = plt.subplots(1, 1, figsize=(10, 8)) 13 ax.grid() 14 ax.set_xlabel(‘X‘) 15 ax.set_ylabel(‘Y‘) 16 for i in range(nb_samples): 17 if Y[i] == 0: 18 ax.scatter(X[i, 0], X[i, 1], marker=‘o‘, color=‘r‘) 19 else: 20 ax.scatter(X[i, 0], X[i, 1], marker=‘^‘, color=‘b‘) 21 plt.show() 22 23 def show_classification_areas(X, Y, lr): 24 x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5 25 y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5 26 xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02), np.arange(y_min, y_max, 0.02)) 27 Z = lr.predict(np.c_[xx.ravel(), yy.ravel()]) 28 Z = Z.reshape(xx.shape) 29 plt.figure(1, figsize=(10, 8)) 30 plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Pastel1) 31 # Plot also the training points 32 plt.scatter(X[:, 0], X[:, 1], c=np.abs(Y - 1), edgecolors=‘k‘, cmap=plt.cm.coolwarm) 33 plt.xlabel(‘X‘) 34 plt.ylabel(‘Y‘) 35 plt.xlim(xx.min(), xx.max()) 36 plt.ylim(yy.min(), yy.max()) 37 plt.xticks(()) 38 plt.yticks(()) 39 plt.show() 40 41 if __name__ == ‘__main__‘: 42 # Create dataset 43 X, Y = make_classification(n_samples=nb_samples, n_features=2, n_informative=2, n_redundant=0, 44 n_clusters_per_class=1) 45 # Show dataset 46 show_dataset(X, Y) 47 # Split dataset 48 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25) 49 # Create logistic regressor 50 lr = LogisticRegression() 51 lr.fit(X_train, Y_train) 52 print(‘Logistic regression score: %.3f‘ % lr.score(X_test, Y_test)) 53 # Compute CV score 54 lr_scores = cross_val_score(lr, X, Y, scoring=‘accuracy‘, cv=10) 55 print(‘Logistic regression CV average score: %.3f‘ % lr_scores.mean()) 56 # Show classification areas 57 show_classification_areas(X, Y, lr)
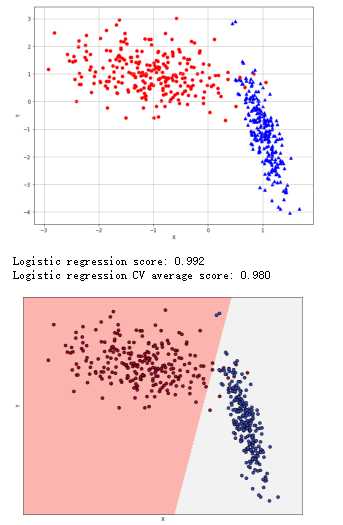
随机梯度下降法:

1 from __future__ import print_function 2 3 import numpy as np 4 import matplotlib.pyplot as plt 5 6 from sklearn.datasets import make_classification 7 from sklearn.linear_model import SGDClassifier 8 from sklearn.model_selection import cross_val_score 9 10 11 # For reproducibility 12 np.random.seed(1000) 13 14 nb_samples = 500 15 16 def show_dataset(X, Y): 17 fig, ax = plt.subplots(1, 1, figsize=(10, 8)) 18 19 ax.grid() 20 ax.set_xlabel(‘X‘) 21 ax.set_ylabel(‘Y‘) 22 23 for i in range(nb_samples): 24 if Y[i] == 0: 25 ax.scatter(X[i, 0], X[i, 1], marker=‘o‘, color=‘r‘) 26 else: 27 ax.scatter(X[i, 0], X[i, 1], marker=‘^‘, color=‘b‘) 28 29 plt.show() 30 31 32 if __name__ == ‘__main__‘: 33 # Create dataset 34 X, Y = make_classification(n_samples=nb_samples, n_features=2, n_informative=2, n_redundant=0, 35 n_clusters_per_class=1) 36 37 # Show dataset 38 show_dataset(X, Y) 39 40 # Create perceptron as SGD instance 41 # The same result can be obtained using directly the class sklearn.linear_model.Perceptron 42 sgd = SGDClassifier(loss=‘perceptron‘, learning_rate=‘optimal‘, n_iter=10) 43 sgd_scores = cross_val_score(sgd, X, Y, scoring=‘accuracy‘, cv=10) 44 print(‘Perceptron CV average score: %.3f‘ % sgd_scores.mean())
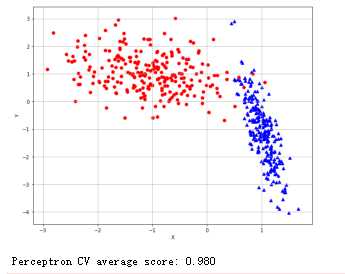
网格搜索找到最优超参数:

1 from __future__ import print_function 2 import numpy as np 3 import multiprocessing 4 from sklearn.datasets import load_iris 5 from sklearn.model_selection import GridSearchCV, cross_val_score 6 from sklearn.linear_model import LogisticRegression 7 # For reproducibility 8 np.random.seed(1000) 9 if __name__ == ‘__main__‘: 10 # Load dataset 11 iris = load_iris() 12 13 # Define a param grid 14 param_grid = [ 15 { 16 ‘penalty‘: [‘l1‘, ‘l2‘], 17 ‘C‘: [0.5, 1.0, 1.5, 1.8, 2.0, 2.5] 18 } 19 ] 20 # Create and train a grid search 21 gs = GridSearchCV(estimator=LogisticRegression(), param_grid=param_grid, 22 scoring=‘accuracy‘, cv=10, n_jobs=multiprocessing.cpu_count()) 23 gs.fit(iris.data, iris.target) 24 # Best estimator 25 print(gs.best_estimator_) 26 gs_scores = cross_val_score(gs.best_estimator_, iris.data, iris.target, scoring=‘accuracy‘, cv=10) 27 print(‘Best estimator CV average score: %.3f‘ % gs_scores.mean())


1 from __future__ import print_function 2 import numpy as np 3 import multiprocessing 4 from sklearn.datasets import load_iris 5 from sklearn.model_selection import GridSearchCV, cross_val_score 6 from sklearn.linear_model import SGDClassifier 7 # For reproducibility 8 np.random.seed(1000) 9 if __name__ == ‘__main__‘: 10 # Load dataset 11 iris = load_iris() 12 13 # Define a param grid 14 param_grid = [ 15 { 16 ‘penalty‘: [‘l1‘, ‘l2‘, ‘elasticnet‘], 17 ‘alpha‘: [1e-5, 1e-4, 5e-4, 1e-3, 2.3e-3, 5e-3, 1e-2], 18 ‘l1_ratio‘: [0.01, 0.05, 0.1, 0.15, 0.25, 0.35, 0.5, 0.75, 0.8] 19 } 20 ] 21 # Create SGD classifier 22 sgd = SGDClassifier(loss=‘perceptron‘, learning_rate=‘optimal‘) 23 # Create and train a grid search 24 gs = GridSearchCV(estimator=sgd, param_grid=param_grid, scoring=‘accuracy‘, cv=10, 25 n_jobs=multiprocessing.cpu_count()) 26 gs.fit(iris.data, iris.target) 27 # Best estimator 28 print(gs.best_estimator_) 29 gs_scores = cross_val_score(gs.best_estimator_, iris.data, iris.target, scoring=‘accuracy‘, cv=10) 30 print(‘Best estimator CV average score: %.3f‘ % gs_scores.mean())

评估分类的指标:含混淆矩阵部分

1 from __future__ import print_function 2 import numpy as np 3 4 from sklearn.datasets import make_classification 5 from sklearn.model_selection import train_test_split 6 from sklearn.linear_model import LogisticRegression 7 from sklearn.metrics import accuracy_score, zero_one_loss, jaccard_similarity_score, confusion_matrix, 8 precision_score, recall_score, fbeta_score 9 # For reproducibility 10 np.random.seed(1000) 11 nb_samples = 500 12 13 if __name__ == ‘__main__‘: 14 # Create dataset 15 X, Y = make_classification(n_samples=nb_samples, n_features=2, n_informative=2, n_redundant=0, 16 n_clusters_per_class=1) 17 18 # Split dataset 19 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25) 20 # Create and train logistic regressor 21 lr = LogisticRegression() 22 lr.fit(X_train, Y_train) 23 print(‘Accuracy score: %.3f‘ % accuracy_score(Y_test, lr.predict(X_test))) 24 print(‘Zero-one loss (normalized): %.3f‘ % zero_one_loss(Y_test, lr.predict(X_test))) 25 print(‘Zero-one loss (unnormalized): %.3f‘ % zero_one_loss(Y_test, lr.predict(X_test), normalize=False)) 26 print(‘Jaccard similarity score: %.3f‘ % jaccard_similarity_score(Y_test, lr.predict(X_test))) 27 # Compute confusion matrix 28 cm = confusion_matrix(y_true=Y_test, y_pred=lr.predict(X_test)) 29 print(‘Confusion matrix:‘) 30 print(cm) 31 print(‘Precision score: %.3f‘ % precision_score(Y_test, lr.predict(X_test))) 32 print(‘Recall score: %.3f‘ % recall_score(Y_test, lr.predict(X_test))) 33 print(‘F-Beta score (1): %.3f‘ % fbeta_score(Y_test, lr.predict(X_test), beta=1)) 34 print(‘F-Beta score (0.75): %.3f‘ % fbeta_score(Y_test, lr.predict(X_test), beta=0.75)) 35 print(‘F-Beta score (1.25): %.3f‘ % fbeta_score(Y_test, lr.predict(X_test), beta=1.25))

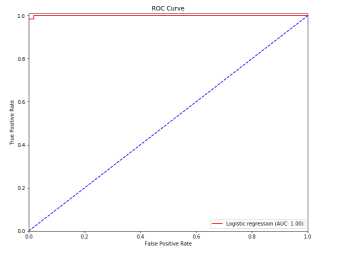
ROC曲线:

1 from __future__ import print_function 2 3 import numpy as np 4 import matplotlib.pyplot as plt 5 6 from sklearn.datasets import make_classification 7 from sklearn.model_selection import train_test_split 8 from sklearn.linear_model import LogisticRegression 9 from sklearn.metrics import roc_curve, auc 10 11 12 # For reproducibility 13 np.random.seed(1000) 14 15 nb_samples = 500 16 17 18 if __name__ == ‘__main__‘: 19 # Create dataset 20 X, Y = make_classification(n_samples=nb_samples, n_features=2, n_informative=2, n_redundant=0, 21 n_clusters_per_class=1) 22 23 # Split dataset 24 X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.25) 25 26 #Create and train logistic regressor 27 lr = LogisticRegression() 28 lr.fit(X_train, Y_train) 29 30 # Compute ROC curve 31 Y_score = lr.decision_function(X_test) 32 fpr, tpr, thresholds = roc_curve(Y_test, Y_score) 33 34 plt.figure(figsize=(10, 8)) 35 36 plt.plot(fpr, tpr, color=‘red‘, label=‘Logistic regression (AUC: %.2f)‘ % auc(fpr, tpr)) 37 plt.plot([0, 1], [0, 1], color=‘blue‘, linestyle=‘--‘) 38 plt.xlim([0.0, 1.0]) 39 plt.ylim([0.0, 1.01]) 40 plt.title(‘ROC Curve‘) 41 plt.xlabel(‘False Positive Rate‘) 42 plt.ylabel(‘True Positive Rate‘) 43 plt.legend(loc="lower right") 44 45 plt.show()
原文:https://www.cnblogs.com/bai2018/p/10581410.html