给定数组arr,arr中所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim代表要找的钱数,求换钱有多少种方法。
arr=[5,10,25,1],aim=0。组成0元的方法有1种,就是所有面值的货币都不用。所以返回1。arr=[5,10,25,1],aim=15。组成15元的方法有6种,分别为3张5元、1张10元+1张5元、1张10元+5张1元、10张1元+1张5元、2张5元+5张1元和15张1元。所以返回6。arr=[3,5],aim=2。任何方法都无法组成2元。所以返回0。
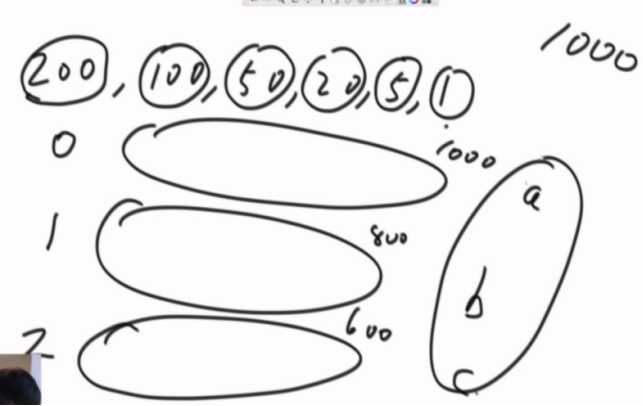
使用0张200的,后面凑出1000的方法数a
使用1张200的,后面凑出 800的方法数b
使用2张200的,后面凑出 600的方法数c
a+b+c全部加起来就是答案。
如果index和aim固定的,只要是后面要计算600那返回值一定是确定的,是个无后效性问题,前面怎么选择不影响后面的操作。但是返回值一样都要重复计算,利用一个map存储之前的结果(缓存)。下次调用,直接取出,不用这么暴力的重复计算。
参数的变化可以囊括返回值的变化,分析可变参数的变化范围
arr[5,3,2],求组成10的方法总数
| 钱的面值 | 位置(数组中的下标) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 目标钱数(aim) |
| 5 | 0 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 4 | |
| 3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 2 | |
| 2 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
原文:https://www.cnblogs.com/tianzeng/p/10585625.html