什么是逻辑回归:
逻辑回归是离散选择法模型之一,属于多重变量分析范畴,是社会学、生物统计学、临床、数量心理学、计量经济学、市场营销等统计实证分析的常用方法。逻辑回归一般用于二分类(Binary Classification)问题中,给定一些输入,输出结果是离散值。例如用逻辑回归实现一个猫分类器,输入一张图片 x ,预测图片是否为猫,输出该图片中存在猫的概率结果 y。从生物学的角度讲:就是一个模型对外界的刺激(训练样本)做出反应,趋利避害(评价标准)。
假设有一个二分类问题,输出为y∈{0,1},而线性回归模型产生的预测值为z=wTx+b是实数值,我们希望有一个理想的阶跃函数来帮我们实现z值到0/1值的转化。
?(z)=???00.51if z < 0if z = 0if z > 0
然而该函数不连续,我们希望有一个单调可微的函数来供我们使用,于是便找到了Sigmoid functionSigmoid function来替代。
?(z)=1+e−z
两者的图像如下图所示(图片出自文献2)
图1:sigmoid & step function
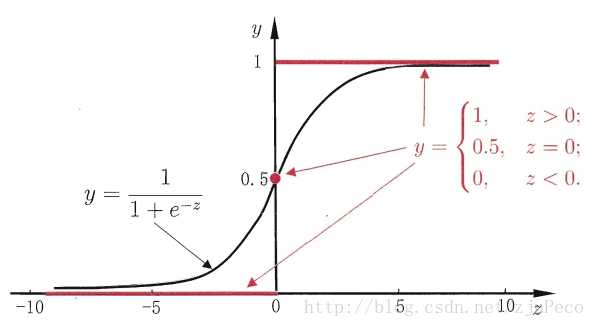
有了Sigmoid fuctionSigmoid fuction之后,由于其取值在[0,1],我们就可以将其视为类11的后验概率估计p(y=1|x)。说白了,就是如果有了一个测试点x,那么就可以用Sigmoid fuctionSigmoid fuction算出来的结果来当做该点x属于类别1的概率大小。
于是,非常自然地,我们把Sigmoid fuctionSigmoid fuction计算得到的值大于等于0.5的归为类别1,小于0.5的归为类别0。
y^={10if ?(z)≥0.5otherwise
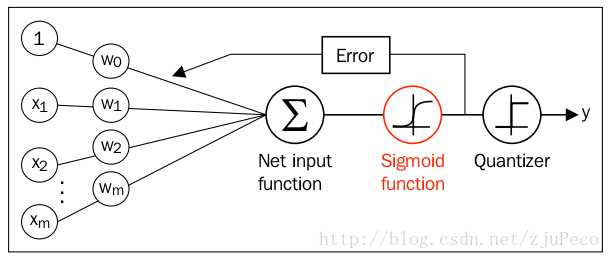
图2:逻辑回归网络
假设有数据3列10行,其中前两列为x1和x2的值,第3列表示y的值;10行表示取了10个样本点。我们可以将这些数据当做训练模型参数的训练样本。
见到训练样本就可以比较直观的理解算法的输入,以及我们如何利用这些数据来训练逻辑回归分类器,进而用训练好的模型来预测新的样本(检测样本)。
从逻辑回归的参数形式,我们可以看到逻辑回归模型中有两个待定参数a(x的系数)和b(常数项),我们现在给出来的数据有两个特征x1, x2,因此整个模型就增加了一项:ax1 + cx2 + b。为了形式上的统一,我们使用带下标的a表示不同的参数(a0表示常数项b并作x0的参数<x0=1>,a1、a2分别表示x1和x2的参数),就可以得到:
这样统一起来后,就可以使用矩阵表示了(比起前面展开的线性表示方式,用矩阵表示模型和参数更加简便,而且矩阵运算的速度也更快):
将上面的式子带入到(1)式,我们就可以得到逻辑回归的另一种表示形式了:
此时,可以很清楚的看到,我们后面的行动都是为了确定一个合适的a(一个参数向量),使得对于一个新来的X(也是一个向量),我们可以尽可能准确的给出一个y值,0或者1.
注:数据是二维的,也就是说这组观察样本中有两个自变量,即两个特征(feature)。
逻辑回归的代价函数
好了,所要用的几个函数我们都有了,接下来要做的就是根据给定的训练集,把参数w给求出来了。要找参数w,首先就是得把代价函数(cost function)给定义出来,也就是目标函数。
我们第一个想到的自然是模仿线性回归的做法,利用误差平方和来当代价函数。
J(w)=∑i12(?(z(i))−y(i))2
其中,z(i)=wTx(i)+b,i表示第ii个样本点,y(i)表示第ii个样本的真实值,?(z(i))表示第ii个样本的预测值。
这时,如果我们将?(z(i))=11+e−z(i)代入的话,会发现这是一个非凸函数,这就意味着代价函数有着许多的局部最小值,这不利于我们的求解。
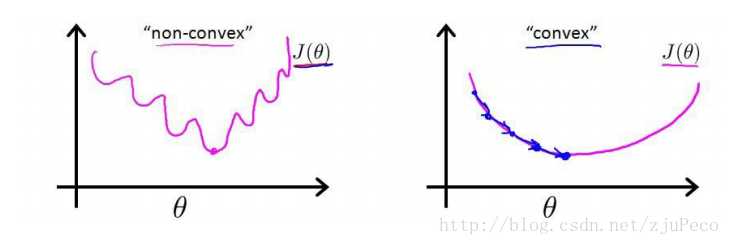
图3:凸函数和非凸函数
那么我们不妨来换一个思路解决这个问题。前面,我们提到了?(z)可以视为类11的后验估计,所以我们有
p(y=1|x;w)=?(wTx+b)=?(z)
p(y=0|x;w)=1−?(z)
其中,p(y=1|x;w)表示给定w,那么x点y=1的概率大小。
上面两式可以写成一般形式
p(y|x;w)=?(z)y(1−?(z))(1−y)
接下来我们就要用极大似然估计来根据给定的训练集估计出参数w。
L(w)=∏ni=1p(y(i)|x(i);w)=∏ni=1(?(z(i)))y(i)(1−?(z(i)))1−y(i)
为了简化运算,我们对上面这个等式的两边都取一个对数
l(w)=lnL(w)=∑ni=1y(i)ln(?(z(i)))+(1−y(i))ln(1−?(z(i)))
我们现在要求的是使得l(w)l(w)最大的ww。没错,我们的代价函数出现了,我们在l(w)前面加个负号不就变成就最小了吗?不就变成我们代价函数了吗?
J(w)=−l(w)=−∑ni=1y(i)ln(?(z(i)))+(1−y(i))ln(1−?(z(i)))
为了更好地理解这个代价函数,我们不妨拿一个例子的来看看
J(?(z),y;w)=−yln(?(z))−(1−y)ln(1−?(z))
也就是说
J(?(z),y;w)={−ln(?(z))−ln(1−?(z))if y=1if y=0
我们来看看这是一个怎么样的函数
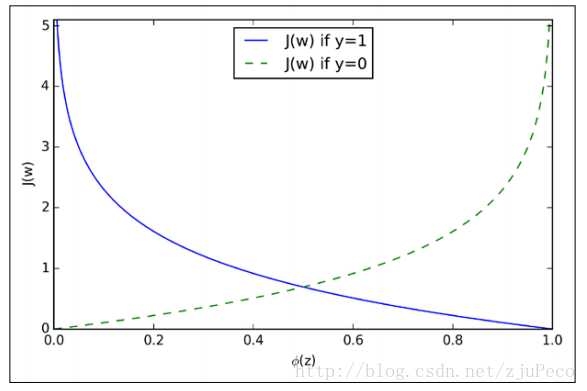
图4:代价函数
从图中不难看出,如果样本的值是1的话,估计值?(z)越接近1付出的代价就越小,反之越大;同理,如果样本的值是0的话,估计值?(z)越接近0付出的代价就越小,反之越大。
利用梯度下降法求参数
在开始梯度下降之前,要这里插一句,sigmoid functionsigmoid function有一个很好的性质就是
?′(z)=?(z)(1−?(z))
下面会用到这个性质。
还有,我们要明确一点,梯度的负方向就是代价函数下降最快的方向。什么?为什么?好,我来说明一下。借助于泰特展开,我们有
f(x+δ)−f(x)≈f′(x)⋅δ
其中,f′(x)和δ为向量,那么这两者的内积就等于
f′(x)⋅δ=||f′(x)||⋅||δ||⋅cosθ
当θ=π时,也就是δ在f′(x)的负方向上时,取得最小值,也就是下降的最快的方向了~
okay?好,坐稳了,我们要开始下降了。
w:=w+Δw, Δw=−η∇J(w)
没错,就是这么下降。没反应过来?那我再写详细一些
wj:=wj+Δwj, Δwj=−η∂J(w)∂wj
其中,wj表示第j个特征的权重;η为学习率,用来控制步长。
重点来了。
∂J(w)wj=−∑ni=1(y(i)1?(z(i))−(1−y(i))11−?(z(i)))∂?(z(i))∂wj=−∑ni=1(y(i)1?(z(i))−(1−y(i))11−?(z(i)))?(z(i))(1−?(z(i)))∂z(i)∂wj=−∑ni=1(y(i)(1−?(z(i)))−(1−y(i))?(z(i)))x(i)j=−∑ni=1(y(i)−?(z(i)))x(i)
所以,在使用梯度下降法更新权重时,只要根据下式即可
wj:=wj+η∑ni=1(y(i)−?(z(i)))x(i)
此式与线性回归时更新权重用的式子极为相似,也许这也是逻辑回归要在后面加上回归两个字的原因吧。
当然,在样本量极大的时候,每次更新权重会非常耗费时间,这时可以采用随机梯度下降法,这时每次迭代时需要将样本重新打乱,然后用下式不断更新权重。
wj:=wj+η(y(i)−?(z(i)))x(i)j,for i in range(n)
也就是去掉了求和,而是针对每个样本点都进行更新。
用python代码实现逻辑回归
‘‘‘ 初始化线性函数参数为1 构造sigmoid函数 重复循环I次 计算数据集梯度 更新线性函数参数 确定最终的sigmoid函数 输入训练(测试)数据集 运用最终sigmoid函数求解分类 ‘‘‘ # -*- coding:utf-8 -*- import numpy as np import matplotlib.pyplot as plt import random def text2num(string): """ :param string: string :return: list """ str_list = string.replace("\n", " ").split(" ") while ‘‘ in str_list: str_list.remove(‘‘) num_list = [float(i) for i in str_list] return num_list def sigmoid(x): """ :param x: 输入需要计算的值 :return: """ return 1.0 / (1 + np.exp(-x)) def data_plot(data_list, weight): """ :param data_list:数据点集合 :param weight: 参数集合 :return: null """ x_data = [list(i[0:2]) for i in data_list if i[2] == 0.0] y_data = [list(i[0:2]) for i in data_list if i[2] == 1.0] x_data = np.reshape(x_data, np.shape(x_data)) y_data = np.reshape(y_data, np.shape(y_data)) linear_x = np.arange(-4, 4, 1) linear_y = (-weight[0] - weight[1] * linear_x) / weight[2] print(linear_y) plt.figure(1) plt.scatter(x_data[:, 0], x_data[:, 1], c=‘r‘) plt.scatter(y_data[:, 0], y_data[:, 1], c=‘g‘) print(linear_x) print(linear_y.tolist()[0]) plt.plot(linear_x, linear_y.tolist()[0]) plt.show() def grad_desc(data_mat, label_mat, rate, times): """ :param data_mat: 数据特征 :param label_mat: 数据标签 :param rate: 速率 :param times: 循环次数 :return: 参数 """ data_mat = np.mat(data_mat) label_mat = np.mat(label_mat) m,n = np.shape(data_mat) weight = np.ones((n, 1)) for i in range(times): h = sigmoid(data_mat * weight) error = h - label_mat weight = weight - rate * data_mat.transpose() * error return weight def random_grad_desc(data_mat, label_mat, rate, times): """ :param data_mat: 数据特征 :param label_mat: 数据标签 :param rate: 速率 :param times: 循环次数 :return: 参数 """ data_mat = np.mat(data_mat) m,n = np.shape(data_mat) weight = np.ones((n, 1)) for i in range(times): for j in range(m): h = sigmoid(data_mat[j] * weight) error = h - label_mat[j] weight = weight - rate * data_mat[j].transpose() * error return weight def improve_random_grad_desc(data_mat, label_mat, times): """ :param data_mat: 数据特征 :param label_mat: 数据标签 :param rate: 速率 :param times: 循环次数 :return: 参数 """ data_mat = np.mat(data_mat) m,n = np.shape(data_mat) weight = np.ones((n, 1)) for i in range(times): index_data = [i for i in range(m)] for j in range(m): rate = 0.0001 + 4 / (i + j + 1) index = random.sample(index_data, 1) h = sigmoid(data_mat[index] * weight) error = h - label_mat[index] weight = weight - rate * data_mat[index].transpose() * error index_data.remove(index[0]) return weight def main(): file = open("/Users/chenzu/Documents/code-machine-learning/data/LR", "rb") file_lines = file.read().decode("UTF-8") data_list = text2num(file_lines) data_len = int(len(data_list) / 3) data_list = np.reshape(data_list, (data_len, 3)) data_mat_temp = data_list[:, 0:2] data_mat = [] for i in data_mat_temp: data_mat.append([1, i[0], i[1]]) print(data_mat) label_mat = data_list[:, 2:3] #梯度下降求参数 weight = improve_random_grad_desc(data_mat, label_mat, 500) print(weight) data_plot(data_list, weight) if __name__ == ‘__main__‘: main()
逻辑回归算法优缺点:
优点:计算代价不高、容易理解和实现
缺点:容易欠拟合,分类精度不高。
适用于数值型和标称型数据。
标称型:标称型目标变量的结果只在有限目标集中取值,如真与假(标称型目标变量主要用于分类)
数值型:数值型目标变量则可以从无限的数值集合中取值,如0.100,42.001等 (数值型目标变量主要用于回归分析)
参考:
斯坦福大学吴恩达的machine learning相关课程
https://blog.csdn.net/zjuPeco/article/details/77165974
https://blog.csdn.net/Julialove102123/article/details/78405261
谈谈对机器学习中逻辑回归的理解(Logistic Regression)
原文:https://www.cnblogs.com/berlinss/p/10586995.html