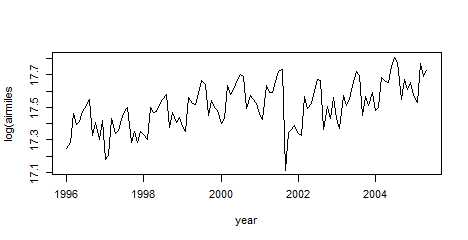
library(TSA) win.graph(width = 4.875,height = 2.5,pointsize = 8) data(airmiles) plot(log(airmiles),ylab = ‘log(airmiles‘,xlab = ‘year‘)
#美国航空的每月客运里程:1996年1月~2005年5月
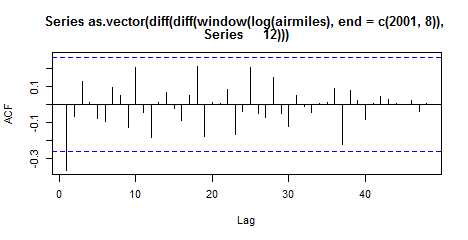
as.vector(diff(diff(window(log(airmiles),end = c(2001,8)),12))),lag.max = 48)
#干预期(1-B)(1-B12)log(航空客运里程)的样本ACF
air.ma1 <- arimax(log(airmiles),order = c(0,1,1),
seasonal = list(order = c(0,1,1),period = 12
),xtransf = data.frame(I911 = 1*(seq(airmiles)==69),
I911 = 1*(seq(airmiles)==69)),
transfer = list(c(0,0),c(1,0)),xreg = data.frame(
Dec96 = 1*(seq(airmiles)==12),
Jan97 = 1*(seq(airmiles)==13),Dec02 = 1*(seq(airmiles)==84)),
method = ‘ML‘)
air.ma1
#对数化航空客运里程的干预模型的估计

plot(log(airmiles),ylab = ‘Log(airmiles)‘) points(fitted(air.ma1))
#对数化的航空客运里程与拟合值

Nine11p <- 1*(seq(airmiles)==69)
plot(ts(Nine11p*(-0.0949)+filter(Nine11p,filter = 0.8139,method = ‘recursive‘,side = 1)
*(-0.2715),frequency = 12,start = 1996),ylab = ‘9/11‘,type = ‘h‘)
abline(h = 0)
#9.11事件对航空客运量序列所造成影响的估计

指的是一些不规则的观测值,其出现可能源自测量误差与复制误差其中之一,或者两者都有可能,也可能源于基础过程发生了短期性变化。
对于时间序列来说可识别的异常值有两种,可加异常值与新息异常值,简记为AO/IO.
原文:https://www.cnblogs.com/xxupup/p/10588650.html