（%%%hmr）
算法呀那个标签：
（越来越懒得写辽）（所以今天打算好好写一写）
首先（ax+by）k的计算需要用到二项式定理：
对于（x+y）k，有第r+1项的系数为：Tr+1=Cnran-rbr
这样对于（ax+by）k而言，第r+1项的系数就为：akbkCnran-rbr
然而这样算，到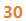
就爆掉了呢！
显然不能暴算，然鹅实际上，二项式定理中的系数T,我们可以看成神奇的杨辉三角形：
这样复杂度就降下来了呀，所以又半途而废了
直接带代码：
#include<iostream> #include<cstdio> #include<algorithm> #define mo 10007 using namespace std; int a,b,k,n,m; int f[1005][1005]; int pow(int a,int k){//快速幂 int ans=1; while(k){ if(k&1)ans=ans*a%mo; a=a*a%mo;k>>=1; }return ans; } int main() { scanf("%d%d%d%d%d",&a,&b,&k,&n,&m); a%=mo;b%=mo;f[0][0]=1; for(int i=1;i<=k;++i){f[i][0]=1; for(int j=1;j<=i;++j) f[i][j]=(f[i-1][j-1]+f[i-1][j])%mo; } printf("%d\n",f[k][n]*pow(a,n)%mo*pow(b,m)%mo); }
beauty？？
end-
原文：https://www.cnblogs.com/zhuier-xquan/p/10606430.html