还是那一道洛谷的板子题来说吧
其实好几天之前就写了
结果dr实在是太弱了
没有那么多的精力
于是就一直咕咕咕了
哎
今天终于补上来了
这个算法是基于RMQ和欧拉序的算法
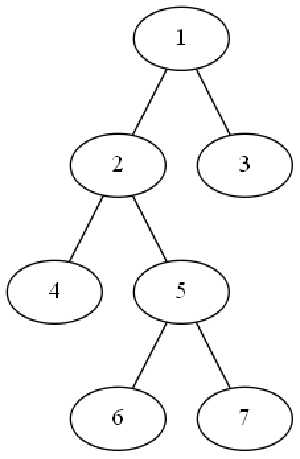

即每经过一次结点就记录一次,
n个结点的树有2n-1个记录
基于Rmq和欧拉序的Lca算法:
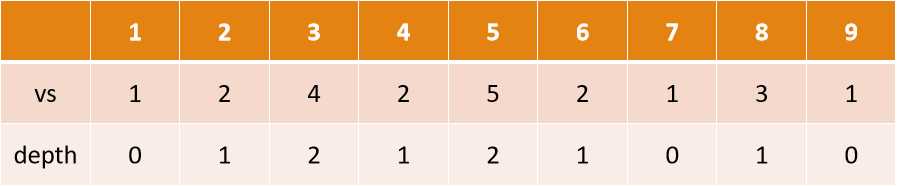
预处理出树的欧拉序,预处理id,vs,depth数组
id[u]表示结点u第一次被访问时的下标,
vs[i]表示欧拉序中第i个结点的编号,
depth[i]表示欧拉序中第i个结点的深度。
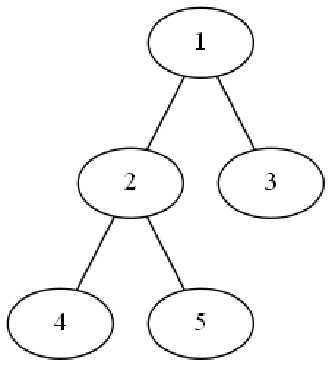
假设dfs顺序1->2->4->5->3

#include<cstdio> #include<algorithm> using namespace std; const int maxn = 500005; const int maxm = 1000005; int head[maxn],nxt[maxm],to[maxm],cnt; int id[maxm],vis[maxm],depth[maxm],tot; int f[maxm][20],lg[maxm]; inline int read() { int sum = 0,p = 1; char ch = getchar(); while(ch < ‘0‘ || ch > ‘9‘) { if(ch == ‘-‘) p = -1; ch = getchar(); } while(ch >= ‘0‘ && ch <= ‘9‘) { (sum *= 10)+= ch - ‘0‘; ch = getchar(); } return sum * p; } void add(int x,int y)//链式前向星--加边 { nxt[++cnt] = head[x]; to[cnt] = y; head[x] = cnt; return; } void dfs(int u,int fa,int dep) { id[u] = ++tot; vis[tot] = u; depth[tot] = dep; for(int i = head[u];i;i = nxt[i]) { int v = to[i]; if(v == fa) continue; dfs(v,u,dep+1); vis[++tot] = u; depth[tot] = dep; } return; } void RMQ() { for(int i = 1;i <= tot;i++) lg[i] = lg[i - 1] + (1 << lg[i - 1] == i); for(int i = 1;i <= tot;i++) f[i][0] = i; for(int j = 1;(1 << j) <= tot;j++) for(int i = 1;i + (1 << j) - 1 <= tot;i++) { int a = f[i][j-1]; int b = f[i + (1 << (j - 1))][j - 1]; if(depth[a] <= depth[b]) f[i][j] = a; else f[i][j] = b; } return; } int st(int x,int y) { int r = id[x]; int l = id[y]; if(r < l) swap(r,l); int k = lg[r - l + 1] - 1; int a = f[l][k]; int b = f[r - (1 << k) + 1][k]; if(depth[a] <= depth[b]) return vis[a]; else return vis[b]; } int main() { int n = read(),m = read(),s = read(); int x,y; for(int i = 1;i < n;i++) { x = read(),y = read(); add(x,y); add(y,x); } dfs(s,0,1); RMQ(); for(int i = 1;i <= m;i++) { x = read(),y = read(); printf("%d\n",st(x,y)); } return 0; }
原文:https://www.cnblogs.com/darlingroot/p/10612077.html