线段树,也叫区间树,是一个完全二叉树,它在各个节点保存一条线段(即“子数组”),因而常用于解决数列维护问题,基本能保证每个操作的复杂度为O(lgN)。
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
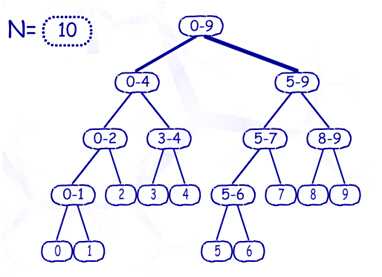
首先介绍构造线段树的方法:让根节点表示区间[0,N-1],即所有N个数所组成的一个区间,然后,把区间分成两半,分别由左右子树表示。不难证明,这样的线段树的节点数只有2N-1个,是O(N)级别的,如图:
typedef struct node { int l; //线段的左端点 int r; //线段的左端点 int value; //线段上的值 }node;
bulid//以节点v为根建树、v对应区间为[l,r] { 对节点v初始化 if (l!=r) { 以v的左孩子为根建树,区间为[l,(l+r)/2] 以v的右孩子为根建树,区间为[(l+r)/2+1,r] } }
#define N 10000 node tree[N]; void bulid(int l, int r, int v) //对结点v进行建立,区间为l~r { tree[v].l = l; tree[v].r = r; if(l == r) { //进行结点的初始化 tree[v].value = a[r]; return; } int mid = (l + r) / 2; bulid(v * 2, l, mid); bulid(v * 2 + 1, mid + 1, r); //根据左右儿子更新当前结点 tree[v].value = tree[v * 2].value + tree[v * 2 + 1].value; }
当在a[i]~a[j]上的所有的元素都加上一个值c的时候
如果a[i]~a[j]刚还是一个完整段的时候,直接将这个段的value值加上c*(r-l+1)
当更新的区间不是一个完整段的时候,采用一种记录增量的方法:给每个节点增加一个域:int add,记录更新操作的增量c,初始的时候add均为0,比如当对2~5区间更新后,给该结点的add加上一个值c,再下次要对2~3结点进行更新或查询时,再将add传递到下面的孩子结点中去
完整的更新树代码如下:
typedef struct node { int l; //线段的左端点 int r; //线段的左端点 int value; //线段上的值 int add; }node; void update(int v, int r, int l, int m)//更新区间l~r加上数m { if(tree[v].l == l && tree[v].r == r) { //找到,更新并记录增量 tree[v].value += m * (r - l + 1); tree[v].add = m; return; } if(tree[v].add) { tree[2 * v].add += tree[v].add; tree[2 * v + 1].add += tree[v].add; tree[v].add = 0; } int mid = (tree[v].l + tree[v].r) / 2; if(r <= mid) { update(v * 2, l, r, m); //只对左儿子更新 } else { if(l > mid) { update(v * 2 + 1, l, r, m); //只对右儿子更新 } else { //区间横跨左右儿子区间,对其两者均进行更新 update(v * 2, l, mid, m); update(v * 2 + 1, mid + 1, r, m); } } }
查询区间l~r上的value值
void query(int v, int l, int r) //当前查询结点为v,要查询的区间为l~r { if(tree[v].l == l && tree[v].r == r) { ans += tree[v].value; return; } if(tree[v].add) { tree[v * 2].add += tree[v].add; tree[v * 2 + 1].add += tree[v].add; tree[v].add = 0; } int mid = (tree[v].l + tree[v].r) / 2; if(r <= mid) { query(v * 2, l, r); //要查询的区间都在左儿子 } else { if(l > mid) { query(v * 2 + 1, l, r); //要查询的区间都在左儿子 } else { //要查询的区间横跨左右孩子 query(v * 2, l, mid); query(v * 2 + 1, mid + 1, r); } } }
注:
源地址:http://www.cnblogs.com/archimedes/p/segment-tree.html
原文:https://www.cnblogs.com/gogoflower/p/10613867.html