Description
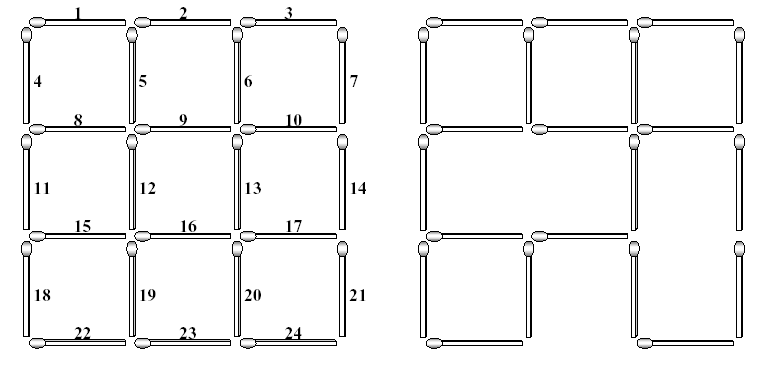
Input
Output
Sample Input
2 2 0 3 3 12 17 23
Sample Output
3 3
题意:t组数据,给出n代表n*n的网格,给一个值k,然后k个值,表示去掉k所代表的边,问还需要最少去掉几条边可以使得网格中没有正方形。
思路:
评估函数:每出现一个正方形,就删去其含有的边,然后继续扫描正方形,这样计数出来的次数比实际需要次数小(因为一次删去了多条边)
对于网格中正方形的枚举:
①先枚举正方形大小,1 <= size <= n;
②枚举网格每行最左边的火柴
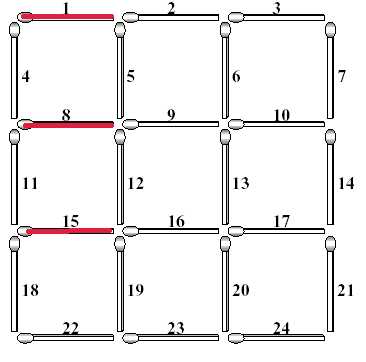
③对于每个行位置,枚举该行可以成为该size大小正方形的最左边火柴
④标记该正方形的所有上边界和下边界(知道size和上边界最左火柴很容易求得)
标记该正方形的所有左边界和有边界
(代码借鉴网上,侵删)
stick【i】表示含有i火柴的正方形编号
square【i】表示i正方形所含火柴编号

#include<iostream> #include<cstdio> #include<vector> #include<cstring> using namespace std; int t; int totsquare,totstick,base; vector<int>stick[65],square[65]; int n,k; int ans; int exi[65],tmp[65]; int cal() { int res = 0; for(int i=1;i<=totsquare;i++)tmp[i] = exi[i]; for(int i=1;i<=totsquare;i++)if(!tmp[i]) { res++; for(int j=0;j<square[i].size();j++) { for(int l=0;l<stick[square[i][j]].size();l++) { tmp[stick[square[i][j]][l]]--; } } } return res; } bool dfs(int sum,int lim) { if(sum + cal() > lim)return 0; int tmp = 1; while(exi[tmp] < 0 && tmp <= totsquare)tmp++; if(tmp > totsquare) { ans = min(ans,sum); return 1; } for(int i=0;i<square[tmp].size();i++) { int sti = square[tmp][i]; for(int j=0;j<stick[sti].size();j++) { exi[stick[sti][j]]--; } if(dfs(sum+1,lim))return 1; for(int j=0;j<stick[sti].size();j++) { exi[stick[sti][j]]++; } } return 0; } int main() { scanf("%d",&t); while(t--) { scanf("%d%d",&n,&k); totsquare = 0,totstick = 2*n*(n+1),base = 2*n+1; for(int i=1; i<65; i++) { stick[i].clear(); square[i].clear(); } for(int sz=1; sz<=n; sz++) { for(int i=1; (i-1)/base+sz<=n; i+=base) { for(int j=i; j-i+sz<=n; j++) { totsquare++; for(int l=j; l-j<sz; l++) // 正方形上下边界标记 { square[totsquare].push_back(l); square[totsquare].push_back(l+sz*base); stick[l].push_back(totsquare); stick[l+sz*base].push_back(totsquare); } for(int l=j+n; (l-j-sz)/base<sz; l+=base) //正方形左右边界标记 { square[totsquare].push_back(l); square[totsquare].push_back(l+sz); stick[l].push_back(totsquare); stick[l+sz].push_back(totsquare); } } } } memset(exi,0,sizeof(exi)); for(int i=1; i<=k; i++) { int t_st; scanf("%d",&t_st); for(int j=0; j<stick[t_st].size(); j++) { exi[stick[t_st][j]]--; } totstick--; } ans = totstick; for(int maxd=0;; maxd++) { if(dfs(0,maxd)) { printf("%d\n",ans); break; } } } }
Square Destroyer-POJ 1084 (IDA*)
原文:https://www.cnblogs.com/iwannabe/p/10633322.html