一.先整理下关于STL里面栈和队列的用法,以及优先队列的基础使用和java里面对于两者的具体使用
栈:一种先进后出的数据结构,只有一个出口,只能 操作最顶端的元素。
C++:

java:
基本操作:
public class Test01 { public static void main(String[] args) { Stack stack=new Stack(); //1.empty()栈是否为空 System.out.println(stack.empty()); //2.peek()栈顶值 3.进栈push() stack.push(new Integer(1)); stack.push("b"); System.out.println(stack.peek()); //4.pop()出栈 stack.pop(); System.out.println(stack.peek()); } }
附一段使用自己使用stack的代码:
import java.util.Scanner; import java.util.Stack; public class Main1{ public static void main(String[]args) { Scanner sc=new Scanner(System.in); while(sc.hasNext()) { String s=sc.nextLine(); Stack <String>stack=new Stack<String>();//定义一个栈 String news[]=s.split(" "); for(int i=0;i<news.length;i++) { stack.push(news[i]);//入栈操作,对于出栈操作应为stack.peak(),注意与C++的区别 } int flag=0; while(!stack.isEmpty()) {//判断栈是否为空 flag++; if(flag==news.length) { System.out.println(stack.pop());//删除栈顶元素并返回删除的栈顶元素,注意与C++里栈的区别 } else System.out.print(stack.pop()+" "); } } } }
队列:队列是一种先进先出的数据结构,从底端加入元素,从顶端取出元素

优先队列:priority_queue
一个拥有权值观念的queue,自动按照元素的权值排列,权值高的排在前面。在缺省情况下,priority_queue是利用一个max_heap
完成的。
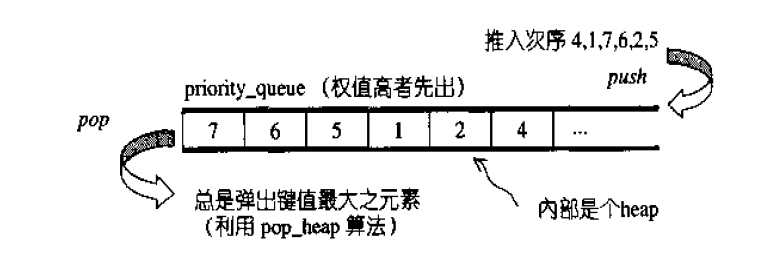

普通方法:
java队列较为复杂暂不赘述
二.栈与队列的底层实现 链式
下面两个底层实现,与课堂上面的实现不太一样,根据自己的使用情况针对具体的题敲的,都已AC。如果使用底层实现代码,建议阅读后使用。
栈:通过一道之前自己手敲的底层实现题注释一下
#include<bits/stdc++.h> using namespace std; template <class T> struct Node { T data; Node<T> *next; }; template<class T>///定义栈 class LinkStack { private: Node<T> *top; public: LinkStack(){top=NULL;}///没有头节点的 ~LinkStack(); void Push(T x); void Pop(); T Get_Top(); int Empty(){if(top==NULL) return 1;return 0;} }; /* 析构函数 */ template<class T> LinkStack<T>::~LinkStack() { while(top) { Node<T> *p; p=top; top=top->next; delete p; } } /* 入栈 */ template<class T> void LinkStack<T>::Push(T x) { Node<T> *s; s=new Node<T>; s->data=x; s->next=top; top=s; } /* 删除 */ template<class T> void LinkStack<T>::Pop()///注意此处的pop删除有返回值,而STL里面没有,此题不需要可忽略 { if(top==NULL) throw "下溢"; T x=top->data; Node<T> *p; p=top; top=top->next; delete p; return ; //return x; } /* 出栈 */ template<class T> T LinkStack<T>::Get_Top() { if(top==NULL) throw "栈空"; return top->data; } char str[1000]; void match(LinkStack<char>&s,char str[]) { char e; for(int i=0;str[i]!=NULL;i++) { switch(str[i]) { case ‘(‘: case ‘[‘: case ‘{‘: s.Push(str[i]); break; case ‘)‘: case ‘]‘: case ‘}‘: if(s.Empty()){ printf("Extra right brackets\n"); return ; } else e=s.Get_Top(); if(e==‘(‘&&str[i]==‘)‘||e==‘[‘&&str[i]==‘]‘||e==‘{‘&&str[i]==‘}‘) { s.Pop(); break; } else { printf("Brackets not match\n"); return ; } } } if(s.Empty()) { printf("Brackets match\n"); } else { printf("Extra left brackets\n"); } } int main() { LinkStack<char> My_stack; cin>>str; match(My_stack,str); return 0; }
队列的底层实现:
#include<bits/stdc++.h> using namespace std; template<class T> struct Node { T data; Node<T> *next; }; template<class T> class LinkQueue { private: int length; Node<T> *front,*rear; public: LinkQueue(); ~LinkQueue(); void Insert_Queue(T x); T Delete_Queue(); int Get_Length(){return length;} }; /* 构造队列 */ template<class T> LinkQueue<T>::LinkQueue()///带有头结点 { front=new Node<T>; front->next=NULL; rear=front; length=0; } /* 析构 */ template<class T> LinkQueue<T>::~LinkQueue() { Node<T> *p; while(front) { p=front->next; front=front->next; delete p; } } /* 入队 */ template<class T> void LinkQueue<T>::Insert_Queue(T x) { Node<T>*s; s=new Node<T>; s->data=x; s->next=NULL; rear->next=s; rear=s; length++; } /* 出队 */ template<class T> T LinkQueue<T>::Delete_Queue() { if(rear==front) throw "Error"; Node<T> *p; p=front->next; T x=p->data; front->next=p->next; delete p; if(front->next==NULL) rear=front;///删除只有一个元素的时候 length--; return x; } int main() { int n,m,x; LinkQueue<int> My_queue; while(scanf("%d%d",&n,&m)) { if(n==0&&m==0) break; for(int i=1;i<=n;i++) { scanf("%d",&x); My_queue.Insert_Queue(x); } if(m>My_queue.Get_Length()) { printf("Error\n"); } else { for(int i=1;i<=m;i++) { if(i==m) { printf("%d\n",My_queue.Delete_Queue()); } else { printf("%d ",My_queue.Delete_Queue()); } } } } My_queue.~LinkQueue(); return 0; }
原文:https://www.cnblogs.com/dean-SunPeishuai/p/10636627.html