一般是先求\(\omega\),再求\(\phi\),个别题目是反序的。求\(A\)放在前面或者后面都可以。
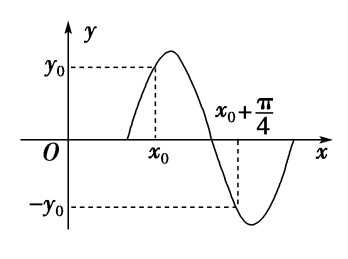
求\(\omega\),往往需要先求\(T\),而求\(T\)时,大多利用最值点和零点求解;更一般的是利用\(x_0\)和\(y_0\)的值求解;
如下图,\(\cfrac{T}{2}=x_0+\cfrac{\pi}{4}-x_0=\cfrac{\pi}{4}\),\(T=\cfrac{\pi}{2}\),从而\(\omega=4\);
\(y=Asin(\omega x+\phi)+B\),最大值为\(M\),最小值为\(m\),则\(A=\cfrac{M-m}{2}\),\(B=\cfrac{M+m}{2}\),
\(\omega\)的给出方式
\(\phi\)的给出方式
已知函数\(f(x)=Asin(\omega x+\phi)(A>0,\omega> 0,0<\phi<\pi)\),其导函数的图象\(f′(x)\)如图所示,则\(f(\cfrac{\pi}{2})\)=【】
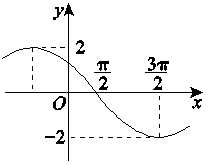
分析:由于\(f'(x)=\omega Acos(\omega x+\phi)\),由\(\cfrac{T}{4}=\cfrac{3\pi}{2}-\cfrac{\pi}{2}=\pi\),故\(T=4\pi\),故\(\omega=\cfrac{2\pi}{4\pi}=\cfrac{1}{2}\),
又由图可知,\(\omega A=\cfrac{1}{2}A=2\),故\(A=4\),又由图\(f'(\cfrac{\pi}{2})=0=2cos(\cfrac{1}{2}\times \cfrac{\pi}{2}+\phi)\),即\(\cfrac{\pi}{4}+\phi=k\pi+\cfrac{\pi}{2}\),\(k\in Z\),故\(\phi=k\pi+\cfrac{\pi}{4}\),令\(k=0\),即\(\phi=\cfrac{\pi}{4}\in (0,\pi)\),
故函数\(f(x)=4sin(\cfrac{1}{2}x+\cfrac{\pi}{4})\),则\(f(\cfrac{\pi}{2})=4\),故选\(D\)。
已知函数\(f(x)=Atan(\omega x+\phi)\),其中\(\omega >0\),\(|\phi|<\cfrac{\pi}{2}\),\(y=f(x)\)的部分图象如图,则\(f(\cfrac{\pi}{24})\)=__________.
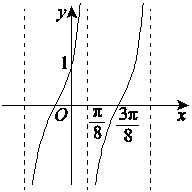
分析:由图可知,\(\cfrac{T}{2}=\cfrac{3\pi}{8}-\cfrac{\pi}{8}=\cfrac{\pi}{4}\),则\(T=\cfrac{\pi}{2}\),故\(\omega=\cfrac{\pi}{T}=2\),
又当\(x=\cfrac{3\pi}{8}\)时,\(2\times \cfrac{3\pi}{8}+\phi=k\pi\),\(k\in Z\),则\(\phi=k\pi-\cfrac{3\pi}{4}\),
令\(k=1\),则\(\phi=\pi-\cfrac{3\pi}{4}=\cfrac{\pi}{4}\in (-\cfrac{\pi}{2},\cfrac{\pi}{2})\),又\(x=0\)时,\(y=1\),
即\(Atan(2\times 0+\cfrac{\pi}{4})=1\),故\(A=1\),即\(f(x)=tan(2x+\cfrac{\pi}{4})\),
故\(f(\cfrac{\pi}{24})=tan(2\times \cfrac{\pi}{24}+\cfrac{\pi}{4})=\sqrt{3}\)。
已知函数\(y=sin(ωx+φ)\) \((ω>0,0<φ<π)\)的最小正周期为\(π\),且函数图象关于点\((-\cfrac{3\pi}{8},0)\)对称,则该函数的解析式为________.
分析:由于函数\(y=sin(ωx+φ)\)的最小正周期为\(π\),故\(\omega=2\),又图象关于点\((-\cfrac{3\pi}{8},0)\)对称,
则\(2\times (-\cfrac{3\pi}{8})+\phi=k\pi\),故\(\phi=k\pi+\cfrac{3\pi}{4}\),\(k\in Z\) ,
当\(k=0\)时,\(\phi=\cfrac{3\pi}{4}\in (0,\pi)\),故解析式为\(y=sin(2x+\cfrac{3\pi}{4})\).
求$y=Asin(\omega x+\phi)+k$类的解析式
原文:https://www.cnblogs.com/wanghai0666/p/10141459.html