题目描述

　　你有一个长为N，宽为2的墙壁，给你两种砖头：一个长2宽1，另一个是L型覆盖3个单元的砖头。如下图：

　　砖头可以旋转，两种砖头可以无限制提供。你的任务是计算用这两种来覆盖N×2的墙壁的覆盖方法。例如一个2×3的墙可以有5种覆盖方法，如下：

　　注意可以使用两种砖头混合起来覆盖，如2×4的墙可以这样覆盖：

　　给定N ，要求计算2×N的墙壁的覆盖方法。由于结果很大，所以只要求输出最后4位。例如2×l3的覆盖方法为13465，只需输出3465即可。如果答案少于4位，就直接输出就可以，不用加0，如N=3时输出5。

输入输出格式

输入格式

　　一行，一个整数N（1≤N≤1000000），表示墙壁的长。

输出格式

　　一行，输出覆盖方法的最后4位，如果不足4位就输出整个答案。

输入输出样例

输入样例

13

 

输出样例

3465

 

题解

　　当你有长为$i$的墙壁时，假设只用第一种砖头，摆放情况如下：

 

　　

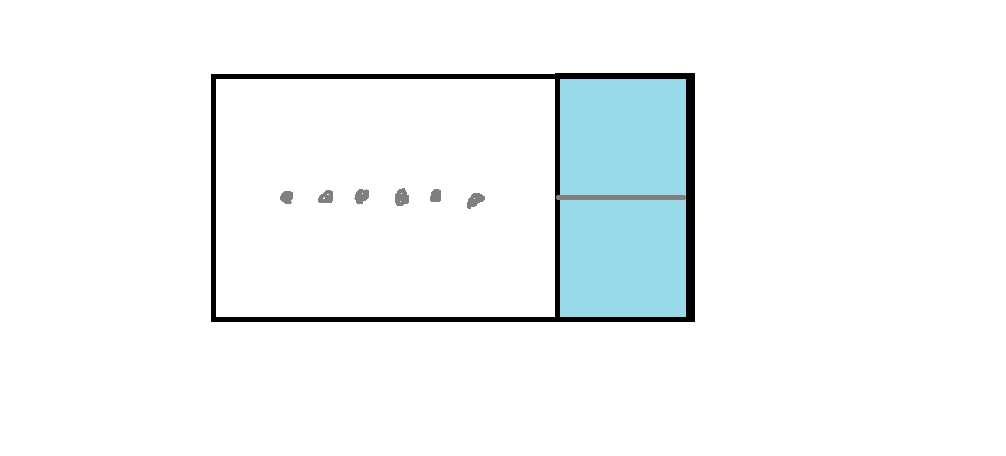
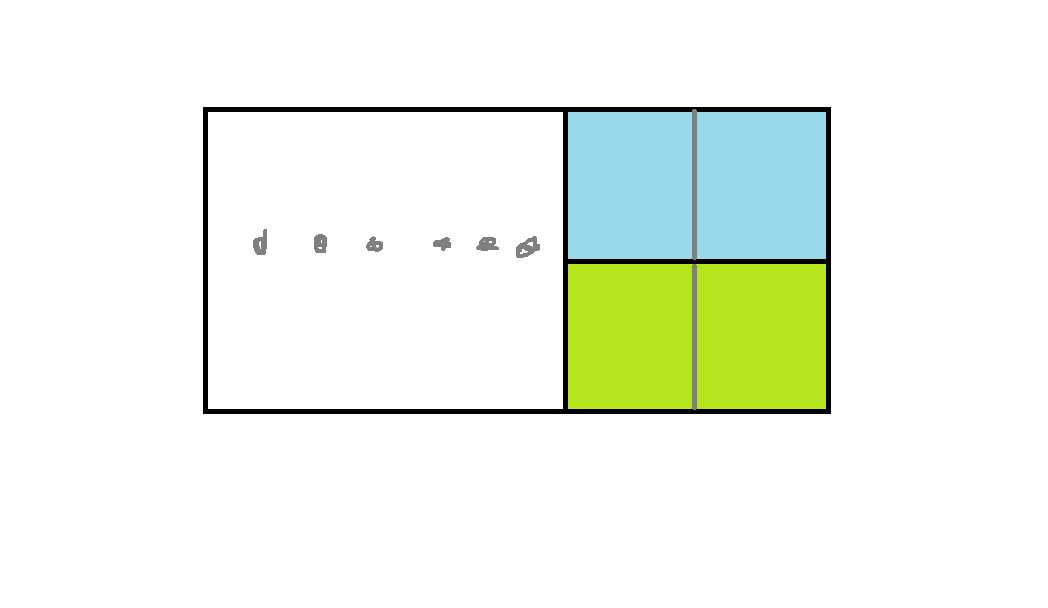
　　设$a[i]$为情况数，易得$a[i]=a[i-1]+a[i-2]$。

　　但如果我们可以用上第二种砖头，那情况就多了很多：

　　

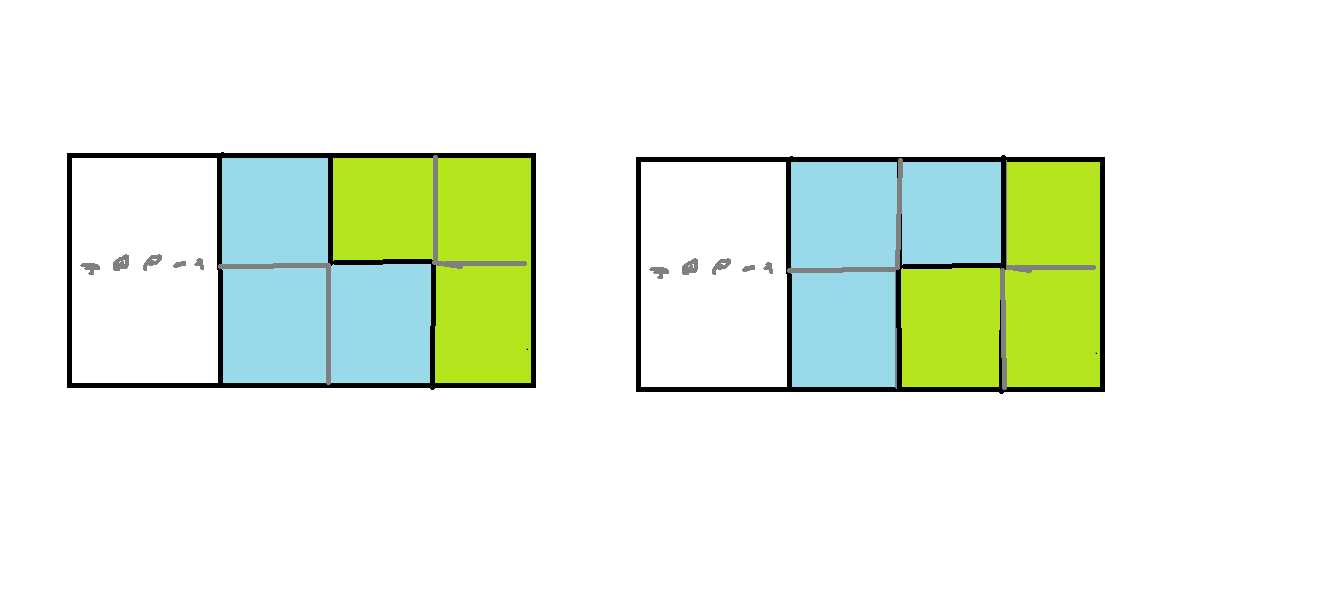
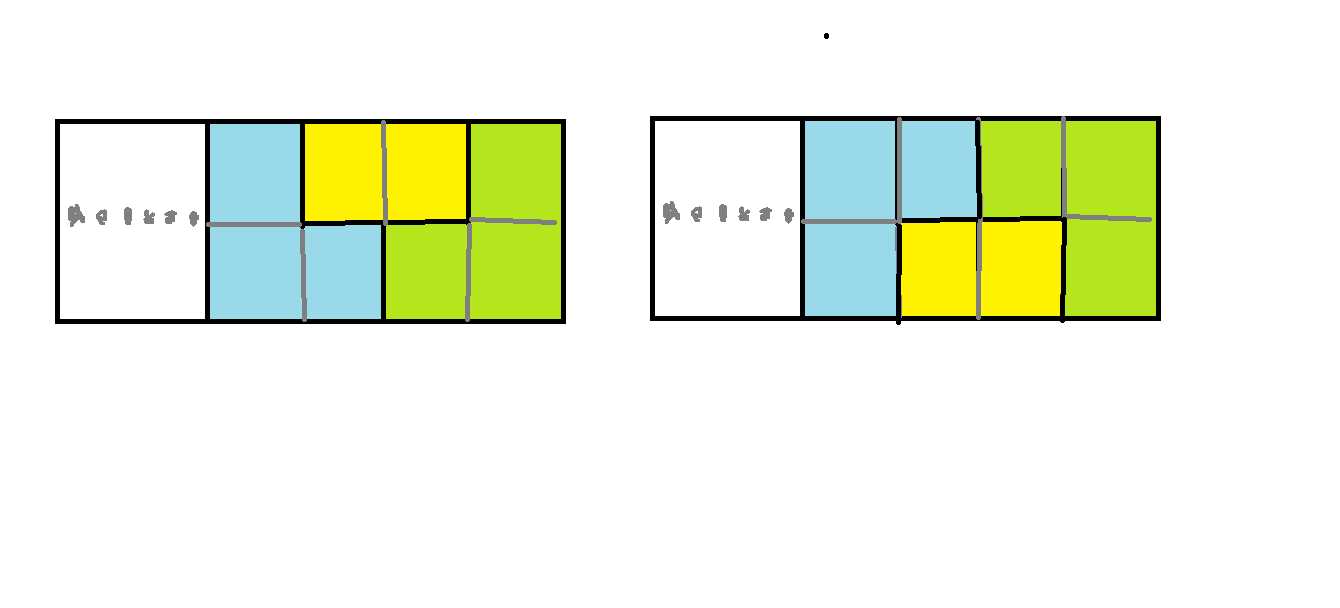
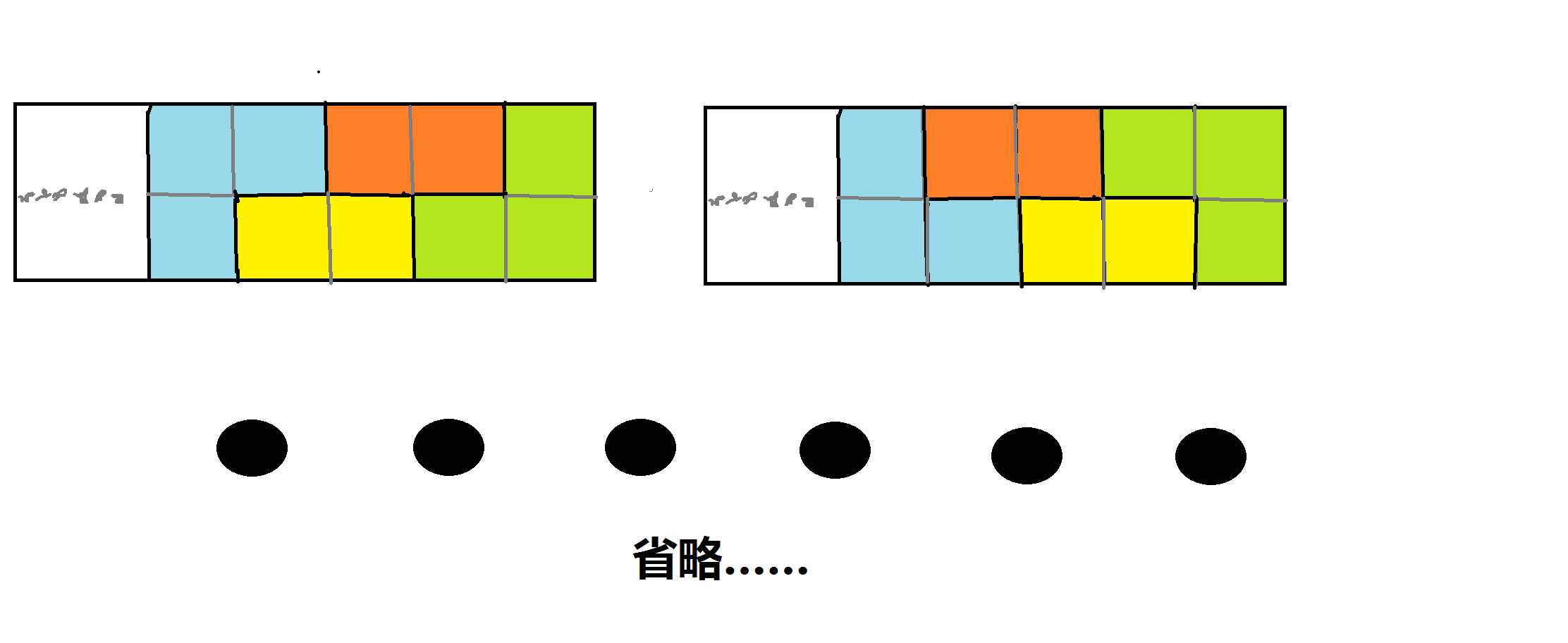
　　设$b[i]$为在$i$后长度为$3$的墙壁放$2$个第二种砖的情况数，易得$b[i]=a[i]\times2$。

　　那如何记录$i$后长度大于$3$的墙壁放第二种砖的情况呢？其实我们可以发现这些情况都等于$b[i]$。

　　容易得到递推式$a[i]=a[i-1]+a[i-2]+\sum_{j=1}^{i-3}b[j]$，前缀和处理一下$b$数组即可。

#include <iostream>
#define MAX_N 1000001

using namespace std;

int n;
int a[MAX_N] = {1,1,2};
int b[MAX_N] = {2,4,8};

int main()
{
    cin >> n;
    for(int i = 3; i <= n; i++)
    {
        a[i] = (a[i - 1] + a[i - 2] + b[i - 3]) % 10000;
        b[i] = (a[i] * 2 + b[i - 1]) % 10000;
    }
    cout << a[n];
    return 0;
}

参考程序

 

 

【题解】覆盖墙壁

原文：https://www.cnblogs.com/kcn999/p/10662540.html