K最近邻算法编写推荐系统
O (log n ),也叫对数时间 ,这样的算法包括二分查找。
O (n ),也叫线性时间 ,这样的算法包括简单查找。
O (n * log n ),这样的算法包括第4章将介绍的快速排序——一种速
度较快的排序算法。
O (n 2 ),这样的算法包括第2章将介绍的选择排序——一种速度较
慢的排序算法。
O (n !),这样的算法包括接下来将介绍的旅行商问题的解决方案
——一种非常慢的算法。
2.1 内存的工作原理
2.2 数组和链表(这个地方没怎么仔细看。以及P50,P51没仔细看)
使用数组意味着所有待办事项在内存中都是相连的(紧靠在
一起的)。

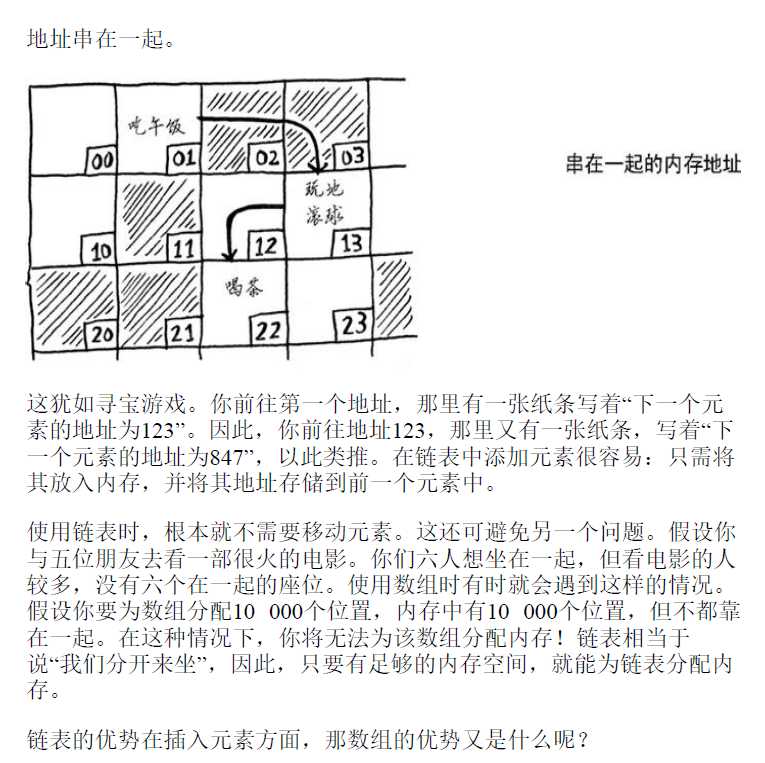
数组的优势是读取方便!!!!!!!!
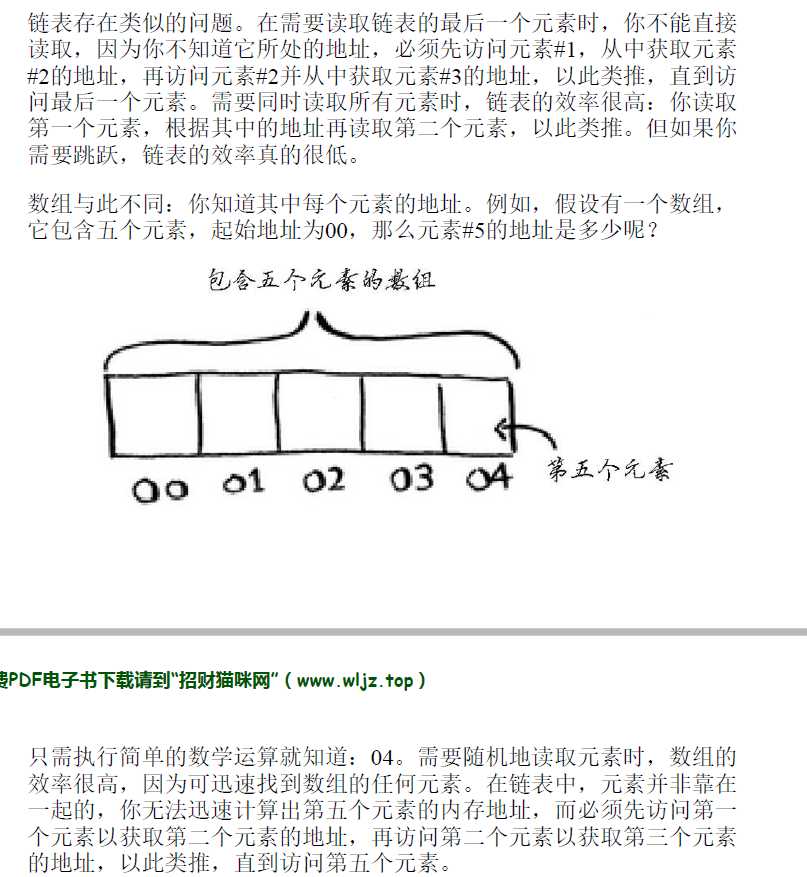
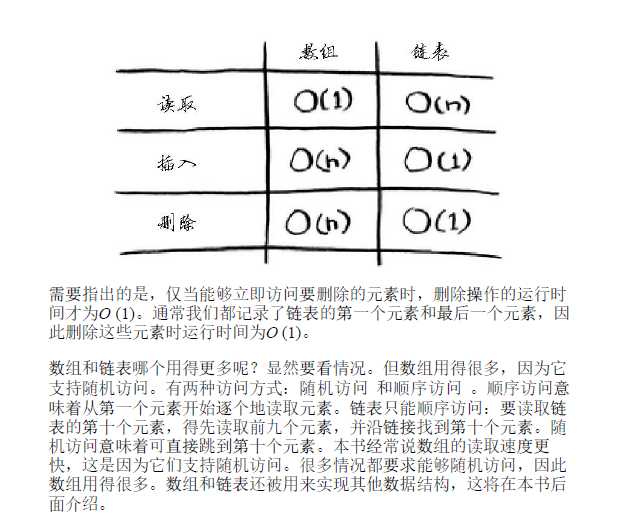
链表存在类似的问题。在需要读取链表的最后一个元素时,你不能直接
读取,因为你不知道它所处的地址,必须先访问元素#1,从中获取元素
#2的地址,再访问元素#2并从中获取元素#3的地址,以此类推,直到访
问最后一个元素。
需要同时读取所有元素时,链表的效率很高:你读取
第一个元素,根据其中的地址再读取第二个元素,以此类推。但如果你
需要跳跃,链表的效率真的很低。
选择排序是一种灵巧的算法,但其速度不是很快。快速排序是一种更快
的排序算法,其运行时间为O (n log n )。
并非每次都需要检查n 个元素。第一次需要检查n 个
元素,但随后检查的元素数依次为n - 1, n – 2, …, 2和1。平均每次
检查的元素数为1/2 × n ,因此运行时间为O (n × 1/2 × n )。但大O表
示法省略诸如1/2这样的常数(有关这方面的完整讨论,请参阅第4
章),因此简单地写作O (n × n )或O (n 2 )。
计算机内存小节:
需要存储多个元素时,可使用数组或链表。
数组的元素都在一起。
链表的元素是分开的,其中每个元素都存储了下一个元素的地址。
数组的读取速度很快。
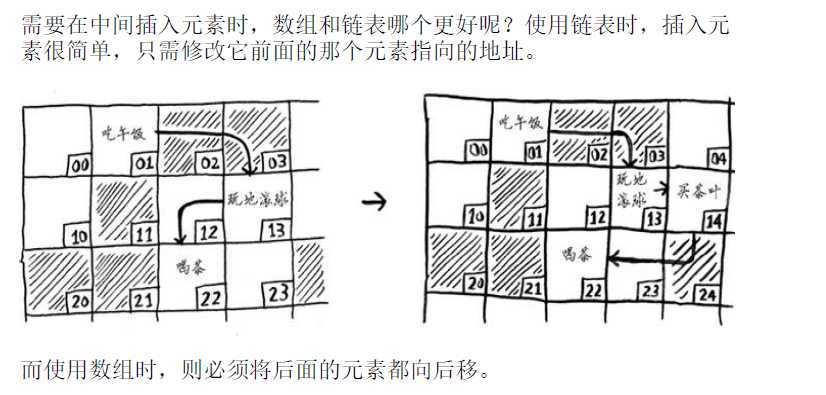
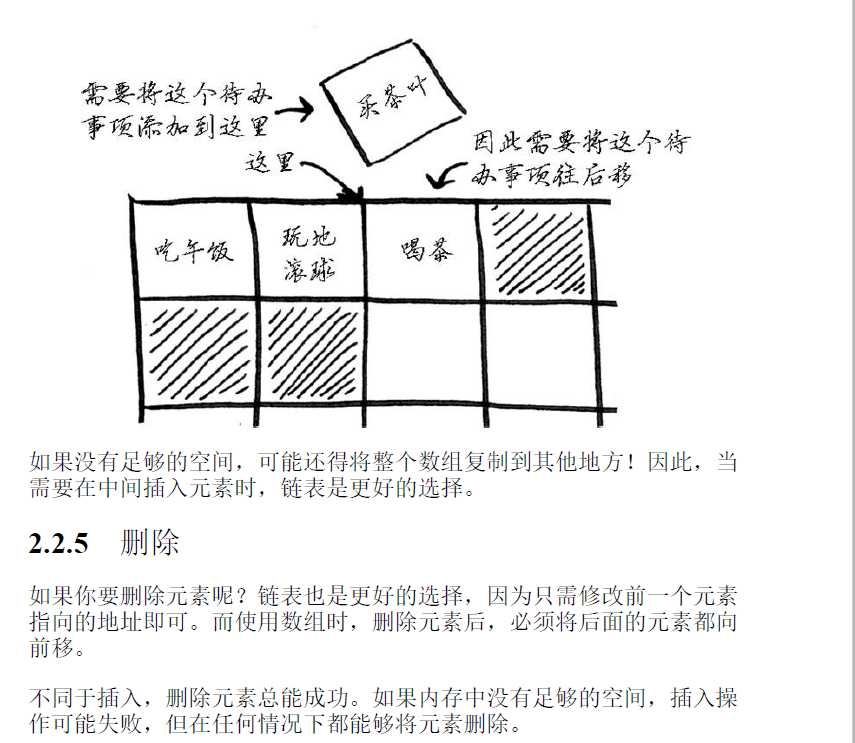
链表的插入和删除速度很快。
在同一个数组中,所有元素的类型都必须相同(都为int、double
等)。
如果使用循环,程序的性能可能更高;如果使用递归,程序可能
更容易理解。如何选择要看什么对你来说更重要
找盒子:
方法一:循环
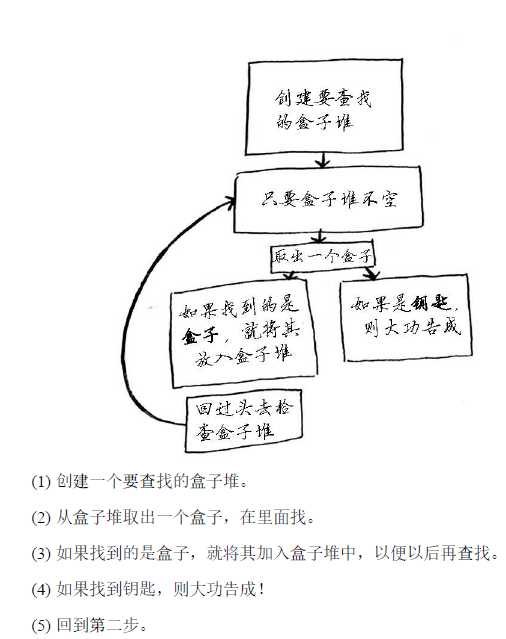
方法二:递归——函数调用自己

递归函数结构:
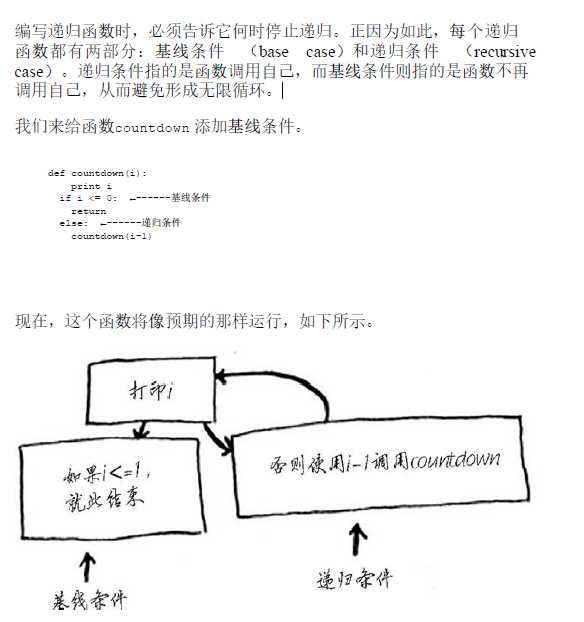
基线条件 (base case)和递归条件 (recursive
case)。
递归条件指的是函数调用自己,而基线条件则指的是函数不再
调用自己,从而避免形成无限循环。
def countdown(i):
print i
if i <= 0: ←------基线条件
return
else: ←------递归条件
countdown(i-1)
调用栈:::::
递归指的是调用自己的函数。
每个递归函数都有两个条件:基线条件和递归条件。
栈有两种操作:压入和弹出。
所有函数调用都进入调用栈。
调用栈可能很长,这将占用大量的内存。
第四章:快速排序
分而治之 (divide and conquer,D&C)——一种著名的递归
式问题解决方法。
问题:均匀地分成方块,且分出的方块要尽可能大
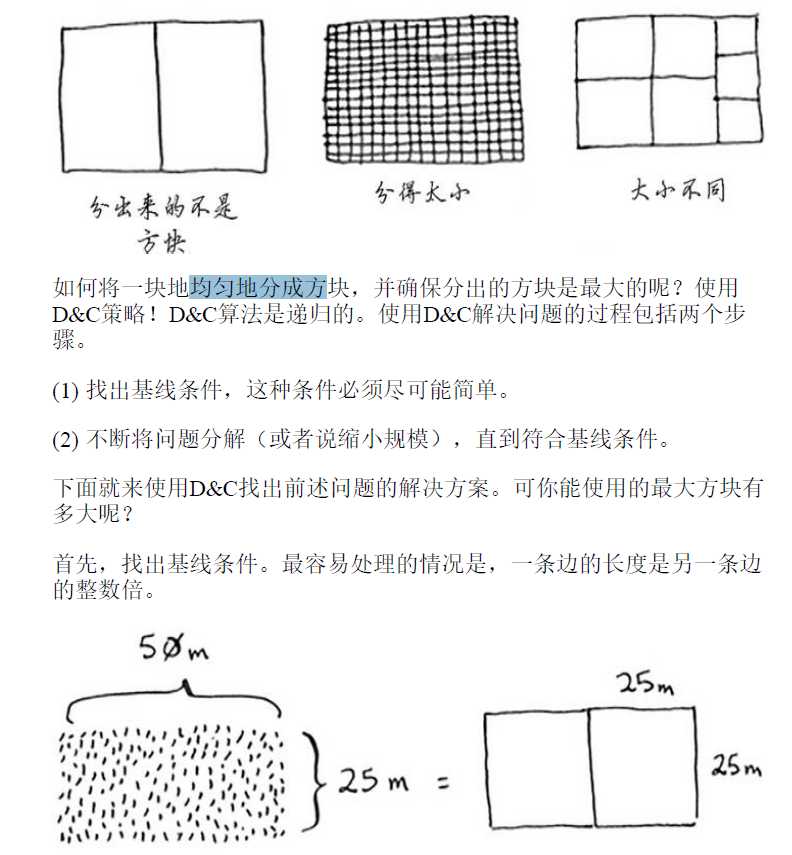
我们希望每次递归调用都必须缩小问题的规模。如何缩小前述问题的规模呢?我们
首先找出这块地可容纳的最大方块,,,,,,,,
我们就 一步步划分——

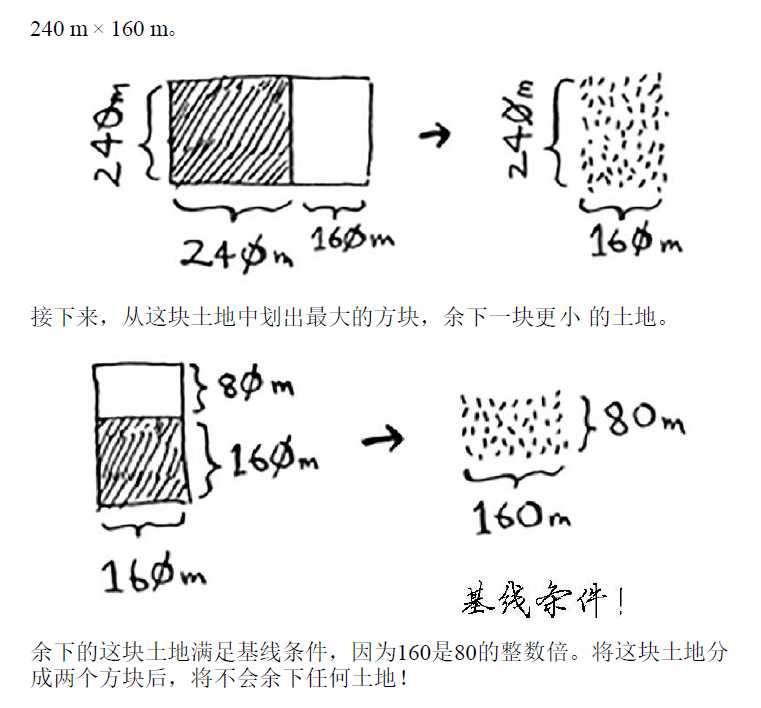
这个基线条件的思想真的很棒!!!!!
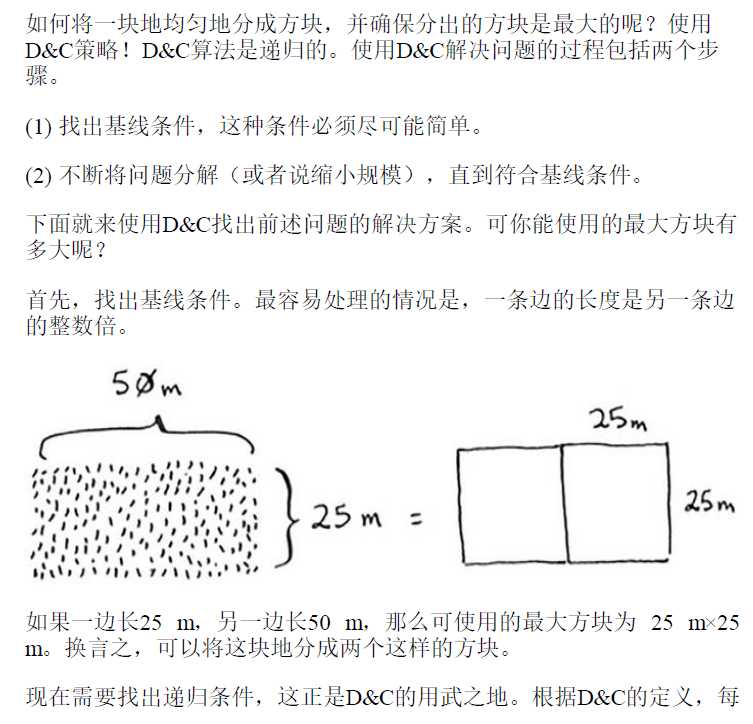
ok,let‘s go on.
这里重申一下D&C的工作原理:
(1) 找出简单的基线条件;
(2) 确定如何缩小问题的规模,使其符合基线条件。
D&C并非可用于解决问题的算法,而是一种解决问题的思路
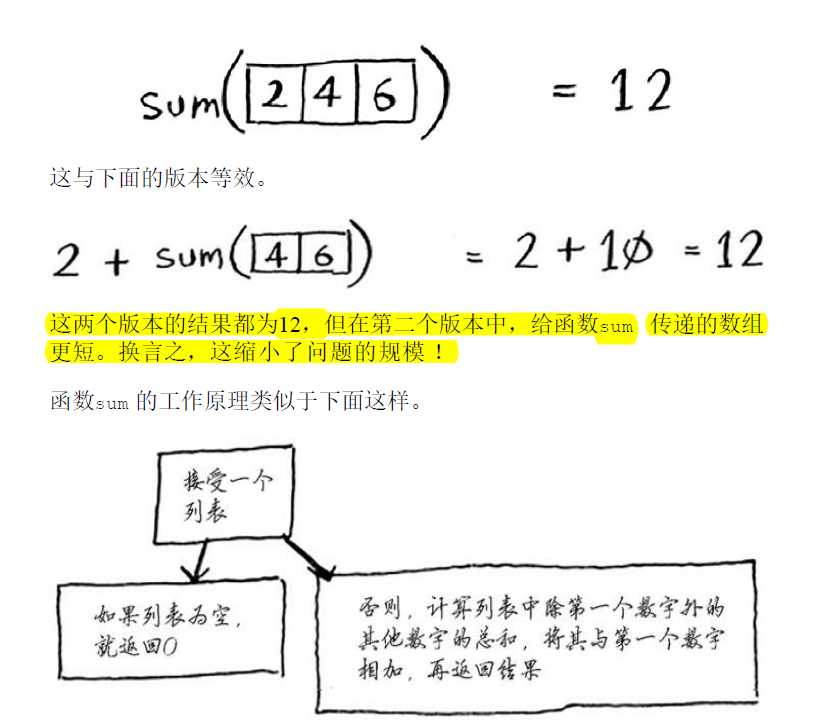
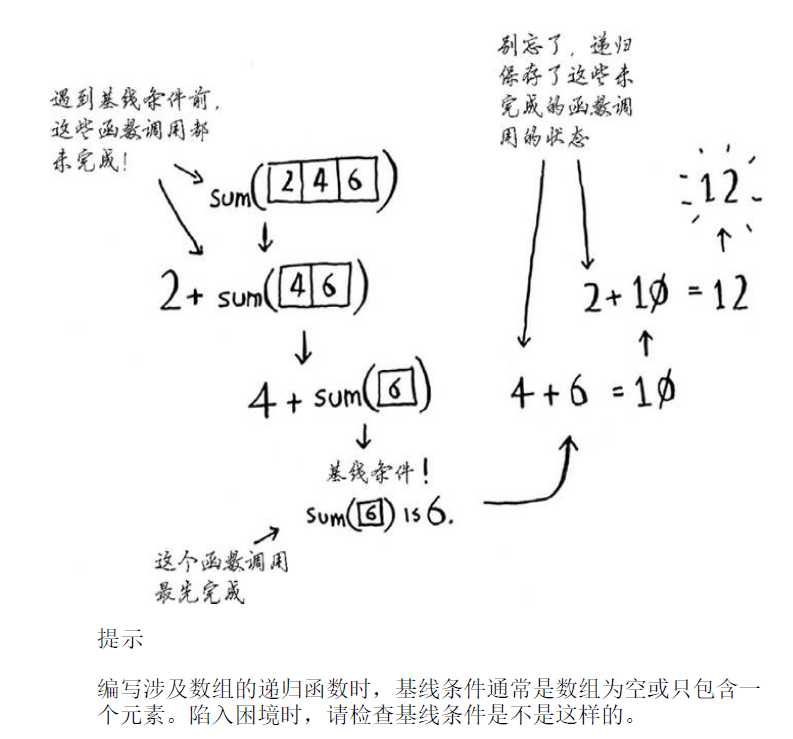
原文:https://www.cnblogs.com/CleverFruitful/p/10648516.html