*在学习后缀自动机之前需要熟练掌握WA自动机、RE自动机与TLE自动机*
后缀自动机 Suffix Automaton (SAM) 是一个用 O(n) 的复杂度构造,能够接受一个字符串所有后缀的自动机。
它最早在陈立杰的 2012 年 noi 冬令营讲稿中提到。
在2013年的一场多校联合训练中,陈立杰出的 hdu 4622 可以用 SAM 轻松水过,由此 SAM 流行了起来。
一般来说,能用后缀自动机解决的问题都可以用后缀数组解决。但是后缀自动机也拥有自己的优点。
1812. Longest Common Substring II 题目大意:给出N(N <= 10)个长度不超过100000的字符串,求他们的最长公共连续子串。 时限:SPOJ上的2s
陈立杰的讲稿中用了 spoj 的1812作为例子,由于 spoj 太慢,所以只有O(n)的算法才能过掉本题,这时就要用到SAM了。
参考网上的各种模板即可。
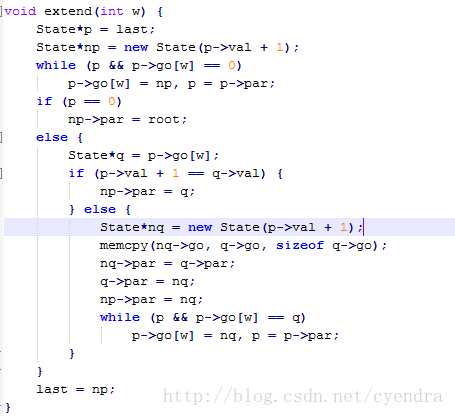
裸的后缀自动机仅仅是一个可以接收子串的自动机,在它的状态结点上维护的性质才是解题的关键。
一个构造好的 SAM 实际上包含了两个图:由 go 数组组成的 DAG 图;由 par 指针构成的 parent 树。
SAM 的状态结点包含了很多重要的信息:
max:即代码中 val 变量,它表示该状态能够接受的最长的字符串长度。
min:表示该状态能够接受的最短的字符串长度。实际上等于该状态的 par 指针指向的结点的 val + 1。
max-min+1:表示该状态能够接受的不同的字符串数。
right:即 end-set 的个数,表示这个状态在字符串中出现了多少次,该状态能够表示的所有字符串均出现过 right 次。
par:par 指向了一个能够表示当前状态表示的所有字符串的最长公共后缀的结点。所有的状态的 par 指针构成了一个 parent 树,恰好是字符串的逆序的后缀树。
parent 树的拓扑序:序列中第i个状态的子结点必定在它之后,父结点必定在它之前。
后缀自动机的遍历。
给一个字符串S,每次可以将它的第一个字符移到最后面,求这样能得到的字典序最小的字符串。
将字符串S拼接为SS,构造自动机,从根结点开始每次走最小编号的边,移动length(S)步就可以找到字典序最小的串。
由于 SAM 可以接受 SS 所有的子串,而字典序最小的字符串也必定是 SS 的子串,因此按照上面的规则移动就可以找到一个字典序最小的子串。
给两个长度小于100000的字符串 A 和 B,求出他们的最长公共连续子串。
先将串 A 构造为 SAM ,然后用 B 按如下规则去跑自动机。
用一个变量 lcs 记录当前的最长公共子串,初始化为0。
设当前状态结点为 p,要匹配的字符为 c,若 go[c] 中有边,说明能够转移状态,则转移并 lcs++;
若不能转移则将状态移动到 p 的 par ,如果仍然不能转移则重复该过程直到 p 回到根节点,并将 lcs 置为 0;
如果在上一个过程中进入了能够转移的状态,则设 lcs 为当前状态的 val。
为什么失配后要移向 par 呢?因为在状态 p 上失配说明该状态的 [min,max] 所表示字符串都不是 B 中的子串,但是比它们短的后缀仍有可能是 B 的子串,而 par 指针恰好指向了该状态的后缀。
在上一题中我们知道了如何求两个串的最长公共子串,本题则是要求多个串的最长公共子串。
本题要用到 parent 树的拓扑序。
首先用第一个串构造 SAM,然后用其他的串匹配它。
SAM 的状态要多维护两个信息:lcs,当多个串的最长公共子串的最后一个字符落在该状态上的长度;nlcs,当前串的最长公共子串的最后一个字符落在该状态上的长度。
我们对每个串的匹配之后,要对每个状态的 lcs 进行维护,显然 lcs=min(lcs, nlcs),而我们最后所求的就是所有状态中 lcs 的最大值。
匹配的过程与上一题相同,但是在匹配过程中,到达状态 p 时得到的 nlcs 未必就是该状态能表示的最长公共子串长,因为如果一个子串出现了n次,那么子串的所有后缀也至少出现了n次。
因此在每个串匹配之后求要按照拓扑序的逆序维护每个状态的 nlcs,使 p->par->nlcs=max(p->nlcs, p->par->nlcs)。
这也是许多新人第一次接触到 SAM 的题。本题可以用各种姿势 AC,但是用 SAM 最轻松。
给出一个字符串,最长2000,q个询问,每次询问[l,r]区间内有多少个不同的字串。
SAM 中的每个状态能够表示的不同子串的个数为 val - 父结点的 val。因此在构造自动机时,用变量 total 记录当前自动机能够表示的不同子串数,对每一次 extend 都更新 total 的值。将这个过程中的每一个 total 值都记录下了就能得到一个表示子串个数表。我们对字符串的每一个后缀都重新构造一遍 SAM 就可以得到一个二维的表。
对每次询问,在表中查找相应的值即可。
给出n个数字,数字很长,用字符串读入,长度总和为10^5。求这n个字符串的所有子串(不重复)的和取模2012 。
题目要对所有不重复的子串进行处理,考虑使用 SAM 来将解决。
将 n 个数字拼接成一个字符串,用不会出现的数字 10 进行分割。
构造完之后按照拓扑序计算每个状态上的 sum 与 cnt,sum 表示以当前状态为结尾的子串的和,cnt 表示有多少种方法到达当前结点。
设父结点为 u 向数字 k 移动到的子结点为 v, 显然结点 v 的状态要在 sum 上增加 add=u->sum*10+u->cnt*k。即 u 的能表示的数字总和乘上10再加上到达 v 的方法总数乘上当前的个位数字 k。
最后答案就是将所有状态的 sum 求和。
给一个字符串S,令F(x)表示S的所有长度为x的子串中,出现次数的最大值。求F(1)..F(Length(S)) 。
在拓扑序的逆序上维护每个状态的 right,表示当前状态的出现次数。
最后当前用每个状态的 right 来更新 f[val],即当前状态能表示的最长串的出现次数。
最后用 f[i] 依次去更新 f[i-1] 取最大值,因为若一个长度为 i 的串出现了 f[i] 次,那么长度为 i-1 的串至少出现 f[i] 次。
给出两个串,问这两个串的所有的子串中(重复出现的,只要是位置不同就算两个子串),长度大于等于k的公共子串有多少个。
先对第一个串构造 SAM,通过状态的 right 与 val 可以轻松求出它能表示的所有子串数。现在的问题是如何满足条件。
用第二个串对 SAM 做 LCS,当前状态 LCS >= K 时,维护状态上的 cnt++,表示该状态为大于K且最长公共串的结尾的次数为 cnt 次。
统计最长公共子串的状态中满足条件的个数 ans+=(lcs-max(K,p->mi)+1)*p->right
匹配结束后,用拓扑序的逆序维护每个状态父结点 cnt,此时 cnt 的含义为该状态被包含的次数。
统计不是最长公共子串的状态但是被子串包含的个数,ans+=p->cnt*(p->par->val - max(K,p->par->mi)+1)*p->par->right,用父结点被包含的次数乘以满足条件的串数累加到答案中。
给出一个字符串,长度为90000。询问q次,每次回答一个k,求字典序第k小的子串。
仍然用拓扑序得到每个状态拥有的不同子串数。
对第k小的子串,按字典序枚举边,跳过一条边则 k 减去该边指向的状态的不同子串数,直到不能跳过,然后沿着该边移动一次,循环这个步骤直到 k变为0。
此时的路径就是字典序第k小的子串。
*这场比赛的出题人是 WJMZBMR 陈立杰*
给出一个字符串s,这里称之为母串,然后再给出n个子串,n<=10^5,子串长度总和不超过10^6。问,对于每一个子串的所有不同的周期性的同构串在母串中出现的次数总和。
将母串构造 SAM,将子串复制拼接到一起然后去掉最后一个字母去跑 SAM。
对满足条件的状态向上维护直到原子串的长度包含在了状态能表示的长度中并用 mark 标记。
然后将该状态的出现次数累加到答案上,如果一个应该累加的状态已经被 mark 过了,就不再累加。
给出两个长度均不超过5000的字符串s1,s2,求这两个串中,都只出现一次的最短公共子串。
对第一个串构造 SAM,用第二个串跑。显然 right 为1的状态就是在第一个串中出现次数为1的子串。
匹配过程总的每进入一个结点,就将结点上的 cnt 加一,表示该状态表示的最长公共串在第二个串的出现次数。
最后按拓扑序逆序求出所有状态的 cnt,若一个结点出现过 cnt 次,那么他的父结点即它的后缀出现次数也要加上 cnt。
最后遍历所有的状态,right 等于 1 且 cnt 等于 1 的状态就是出现次数为1的公共子串,找到其中最短的作为答案即可。

1 #include <iostream> 2 #include <cstring> 3 #include <cstdio> 4 5 using namespace std; 6 typedef long long LL; 7 const int maxn=300000; 8 const int maxm=160000; 9 /*************** 10 SAM 真·模板 11 ***************/ 12 struct State { 13 State *par; 14 State *go[52]; 15 int val; // max,当前状态能接收的串的最长长度 16 int mi; // min,当前状态能接受的串的最短长度,即 par->val+1 17 int cnt; // 附加域,用来计数 18 int right; // right集,表示当前状态可以在多少个位置上出现 19 void init(int _val = 0){ 20 par = 0; 21 val = _val; 22 cnt=0; 23 mi=0; 24 right=0; 25 memset(go,0,sizeof(go)); 26 } 27 int calc(){ // 表示该状态能表示多少中不同的串 28 if (par==0) return 0; 29 return val-par->val; 30 } 31 }; 32 State *root, *last, *cur; 33 State nodePool[maxn]; 34 State* newState(int val = 0) { 35 cur->init(val); 36 return cur++; 37 } 38 //int total; // 不同的子串个数。 39 void initSAM() { 40 //total = 0; 41 cur = nodePool; 42 root = newState(); 43 last = root; 44 } 45 void extend(int w) { 46 State* p = last; 47 State* np = newState(p->val + 1); 48 np->right=1; // 设置right集 49 while (p && p->go[w] == 0) { 50 p->go[w] = np; 51 p = p->par; 52 } 53 if (p == 0) { 54 np->par = root; 55 //total+=np->calc(); 56 } 57 else { 58 State* q = p->go[w]; 59 if (p->val + 1 == q->val) { 60 np->par = q; 61 //total+=np->calc(); 62 } 63 else { 64 State* nq = newState(p->val + 1); 65 memcpy(nq->go, q->go, sizeof(q->go)); 66 //total -= q->calc(); 67 nq->par = q->par; 68 q->par = nq; 69 np->par = nq; 70 //total += q->calc()+nq->calc()+np->calc(); 71 while (p && p->go[w] == q) { 72 p->go[w] = nq; 73 p = p->par; 74 } 75 } 76 } 77 last = np; 78 } 79 80 int d[maxm]; 81 State* b[maxn]; 82 void topo(){ // 求出parent树的拓扑序 83 int cnt=cur-nodePool; 84 int maxVal=0; 85 memset(d,0,sizeof(d)); 86 for (int i=1;i<cnt;i++) maxVal=max(maxVal,nodePool[i].val),d[nodePool[i].val]++; 87 for (int i=1;i<=maxVal;i++) d[i]+=d[i-1]; 88 for (int i=1;i<cnt;i++) b[d[nodePool[i].val]--]=&nodePool[i]; 89 b[0]=root; 90 } 91 92 void gaoSamInit(){ // 求出SAM的附加信息 93 State* p; 94 int cnt=cur-nodePool; 95 for (int i=cnt-1;i>0;i--){ 96 p=b[i]; 97 p->par->right+=p->right; 98 p->mi=p->par->val+1; 99 } 100 } 101 102 103 char s[maxm]; 104 const int INF=0x3f3f3f3f; 105 int gao(char s[]){ 106 int ans=INF; 107 int cnt=cur-nodePool; 108 int len=strlen(s); 109 int lcs=0; 110 State* p=root; 111 112 for (int i=0;i<len;i++){ 113 int son=s[i]-‘a‘; 114 if (p->go[son]!=0){ 115 lcs++; 116 p=p->go[son]; 117 } 118 else{ 119 while (p&&p->go[son]==0) p=p->par; 120 if (p==0){ 121 lcs=0; 122 p=root; 123 } 124 else{ 125 lcs=p->val+1; 126 p=p->go[son]; 127 } 128 } 129 // TODO: 130 if (lcs>0) p->cnt++; 131 } 132 133 for (int i=cnt-1;i>0;i--){ 134 p=b[i]; 135 // TODO: 136 if (p->right==1&&p->cnt==1) ans=min(ans,p->mi); 137 p->par->cnt += p->cnt; 138 } 139 return ans; 140 }
原文:http://www.cnblogs.com/zinthos/p/3899679.html