一、关系的运算
笛卡尔积/直积A×B={(a , b) | a∈A且b∈B},对于∩和∪都满足分配性。
A×B=B×A ?(A=∅)∨(B=∅)∨(A=B)
R⊆A×B,当(a , b)∈R时称a与b具有关系R,即xRy。A=B时R就是A上的一个二元关系。
例如集合幂集P(A)上的包含关系为P⊆={(x , y) | x∈P(A) ∧y∈P(A) ∧x⊆y}
A上的恒等关系IA={(a , a) | a∈A},(a , b)∈IA当且仅当a=b
A上的全域关系EA={(a , b) | a , b∈A},(a , b)∈EA恒成立
注意:关系是集合!对集合成立的运算对关系都成立,例如<∩>=∅,≤∩≥==
R的定义域(domain)为R中所有有序对第一元素构成的集合;值域(range)为所有有序对第二元素构成的集合
Dom(R-1)=Ran(R),Dom(R)=Ran(R-1)
x的像集(image)为R(x)={y∈B | xRy},子集A1的像集R(A1)={y∈B | xRy对某x∈A1成立},R(∅)=∅
若R、S是A到B的二元关系,对任意a∈A都有像集R(a)=S(a),那么R=S
证明:对任意(a ,b)∈R,b∈R(a)=S(a),故(a ,b)∈S,
R在集合C上的限制R|C={(a , b) | a∈C且(a , b)∈R}
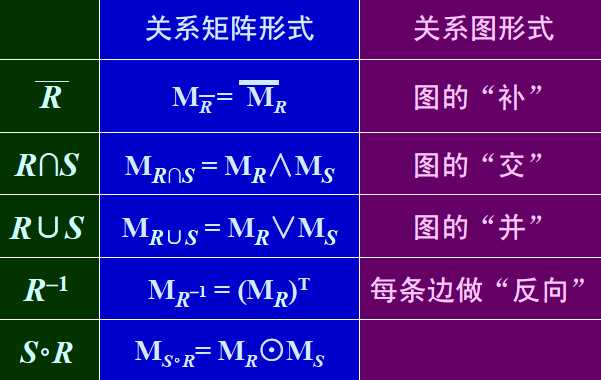
其中矩阵布尔积S○R的计算方法:Rik=1且Skj=1时,(S○R)ij=1。其运算与普通矩阵运算是完全一样的,只不过最后要将所有非0转换为1
(S○R)(A1)=S(R(A1))

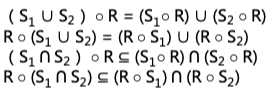
设R为集合A上的关系
A上的关系Rn为:a, b∈A,则aRnb当且仅当存在R中从a到b长为n的道路
A上的关系R∞为:a, b∈A,则aR∞b当且仅当存在R中从a到b的道路
Rn可递归地定义为:
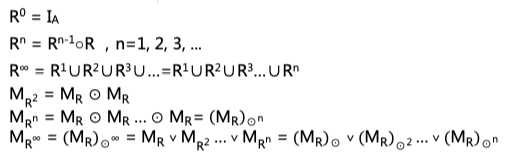
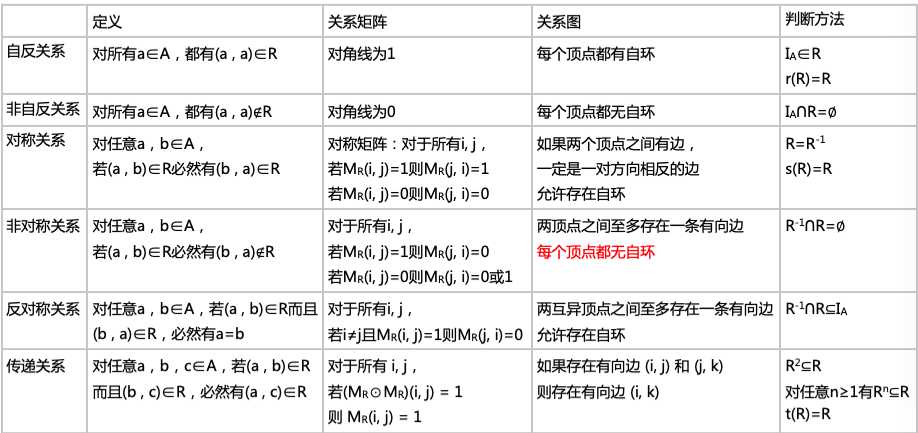
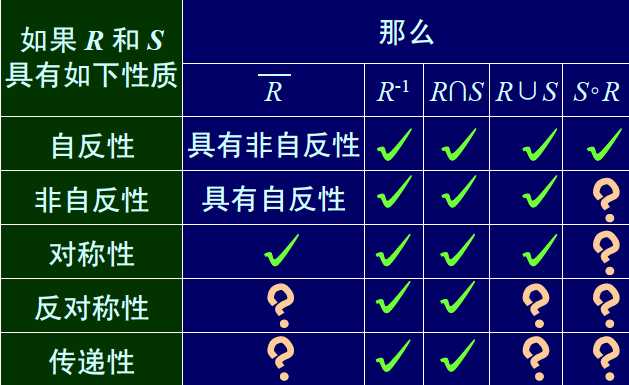
若|A|=n,则A上可定义:
(1)2n×n个不同的关系
(2)2n×n-n个不同的自反关系
(3)2n×n-n个不同的非自反关系
(4)2(n×n-n)/2+n个不同的对称关系
(5)3(n×n-n)/2个不同的非对称关系
(6)2n×3(n×n-n)/2个不同的反对称关系
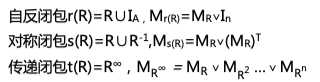
R⊆S时有r(R)⊆r(S)、s(R)⊆s(S)、t(R)⊆t(S)
s(R)和t(R)能保持自反性;r(R)和t(R)能保持对称性;r(R)能保持传递性,s(R)则不一定能保持
(1)rs(R)=r(R∪R-1)=IA∪(R∪R-1)=(R∪IA)∪(R-1∪IA-1)=(R∪IA)∪(R∪IA)-1=s(R∪IA)=sr(R)
(2)rt(R)=r(R∞)=R∞∪IA=(R∪IA)∞=t(R∪IA)=tr(R)
(3)st(R)⊆ts(R),即传递闭包的对称闭包不一定还是传递的,如{(1, 3)}
证明:只需证明①ts(R)具有对称性、②t(R)⊆ts(R)
①的证明:s(R)具有对称性,t(R)能保持对称性,故ts(R)具有对称性
②的证明:R⊆ts(R),ts(R)具有传递性,故t(R)⊆ts(R)

等价关系x~y:自反、对称、传递
R(a)称作a所在的等价类[a]、[a]R
集合{R(a) | a∈A}称作A关于R的商集,记作A/R(即R的所有等价类作为元素的集合),a是R(a)的代表元
aRb,当且仅当R(a)=R(b)
R、S是等价关系时,R∩S一定是等价关系,R∪S则不一定,包含R∪S的最小等价关系是(R∪S)∞
证明:R∩S可以保持自反性、对称性、传递性,因此它是对称关系
R∪S可以保持自反性、对称性,但不一定能保持传递性
因此(R∪S)∞=t(R∪S)肯定也具有自反性、对称性作为R∪S的传递闭包显然也具有传递性 ,因此它是等价关系
对于任何包含R∪S的等价关系T,都是必定具有传递性的,而其中(R∪S)∞作为R∪S的传递闭包必定是最小的
偏序关系:自反、反对称、传递。例如恒等关系IA是就是偏序关系
偏序集:集合A和偏序关系R构成的有序二元组(A , R)
R-1也是偏序关系,称为R的对偶;(A , R-1)称为(A , R)的对偶。
a、b可能可比(a≥b或a≤b),也可能不可比
如果对任意a, b∈A,它们都是可比的,则R称为全序关系/线序关系,(A , R)称为线序集、全序集、链
R-IA是拟序关系
拟序关系:非自反、传递、非对称
逆序集(A , <)中肯定不会存在大于1的圈
R+IA是偏序关系
(1)省略自环
(2)删除可通过传递性省略的有向边
(3)有向边均向上
(4)忽略箭头
(5)所有顶点替换为点
只能表示有限偏序集,例如P({a , b , c})上的⊆关系如图:
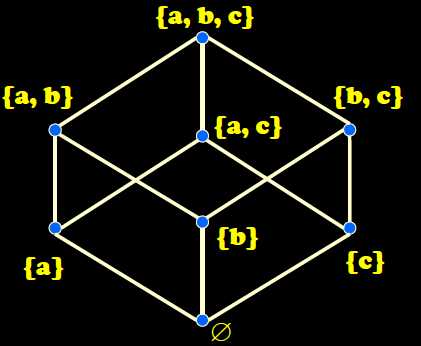
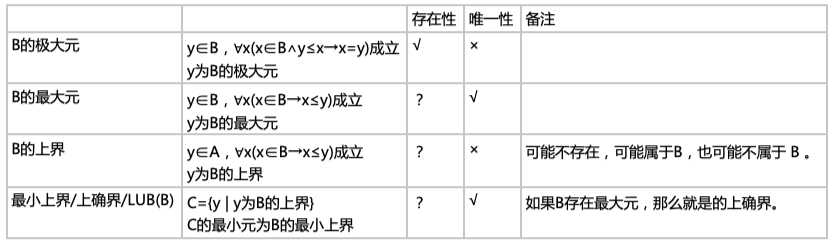
若(A , ≤)是有限非空偏序集,B⊆A
原文:https://www.cnblogs.com/yangyuliufeng/p/10680560.html