后缀树(Suffix tree)是一种数据结构,能快速解决很多关于字符串的问题,缺点是算法复杂难懂且容易出错。
而后缀数组、后缀自动机、后缀仙人掌都是后缀树的替代品。
后缀数组 Suffix Array 是一个一维数组,它将字符串S的n个后缀从小到大排序后把排好序的后缀的开头位置顺次放入数组中。
它可以由倍增算法在O(nlogn)的时间内构造出来。
字符串 S 的子串 r[i..j],i≤j,表示 r 串中从 i 到 j 这一段,也就是顺次排列 r[i],r[i+1],...,r[j]形成的字符串。
后缀是指从某个位置 i 开始到整个串末尾结束的一个特殊子串。
字符串 r 的从第 i 个字符开始的后缀表示为 Suffix(i),也就是 Suffix(i) = r[i..len(r)]。
关于字符串的大小比较,是指通常所说的 “ 字典顺序 ” 比较。
也就是对于两个字符串 u 、v ,令 i 从 1 开始顺次比较 u[i] 和 v[i] ,如果u[i]=v[i] 则令 i 加 1 ,否则若 u[i]<v[i] 则认为 u<v ,u[i]>v[i] 则认为 u>v,比较结束。
如果 i>len(u) 或者 i>len(v) 仍比较不出结果,那么若 len(u)<len(v)则认为 u<v , 若 len(u)=len(v) 则 认 为 u=v ,若 len(u)>len(v) 则 u>v 。
从字符串的大小比较的定义来看, S 的两个开头位置不同的后缀 u 和 v 进行比较的结果不可能是相等,因为 u=v 的必要条件 len(u)=len(v)在这里不可能满足。
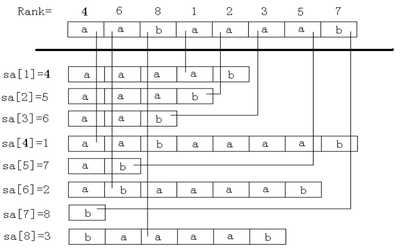
后缀数组 SA 是一个一维数组,它保存 1..n 的某个排列 SA[1],SA[2],……,SA[n],并且保证 Suffix(SA[i]) < Suffix(SA[i+1]),1≤i<n。
也就是将 S 的 n 个后缀从小到大进行排序之后把排好序的后缀的开头位置顺次放入 SA 中。
简单的记忆就是“排第几的是谁”。
名次数组 Rank[i]保存的是 Suffix(i) 在所有后缀中从小到大排列的“名次”。
后缀数组和名次数组为互逆运算。若 sa[i]=j,则 rank[j]=i。
简单的记忆就是“你排第几”。
如何构造后缀数组呢?最直接最简单的方法当然是把S的后缀都看作一些普通的字符串,按照一般字符串排序的方法对它们从小到大进行排序。
复杂度太高不能满足我们的需要。
后缀数组有两种主流的构造方法,倍增算法(double_algorithm)与三分算法(Difference Cover modulo 3)。
倍增算法的思想与ST的思想差不多。将后缀长度依次分为1,2,4,8,。。。,2^k进行排序。进行当前排序时利用到上次的排序结果。
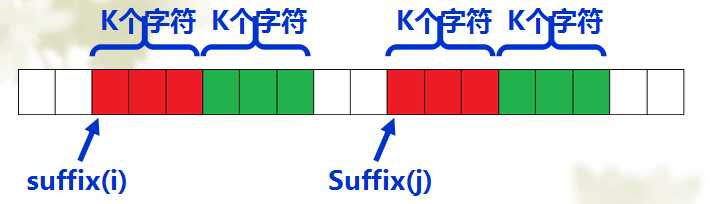
比较suffix(i)和suffix(j)只需先比较红色部分,再比较绿色部分。
倍增算法正是充分利用了各个后缀之间的联系,将构造后缀数组的最坏时间复杂度成功降至O(nlogn)。
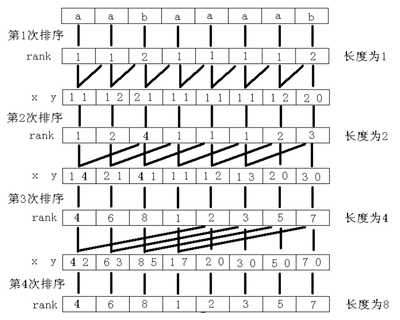
用倍增的方法对每个字符开始的长度为 2^k 的子字符串进行排序,求出排名,即 rank 值。
k 从 0 开始,每次加 1,当 2^k 大于 n 以后,每个字符开始的长度为 2^k 的子字符串便相当于所有的后缀。
并且这些子字符串都一定已经比较出大小,即 rank 值中没有相同的值,那么此时的 rank 值就是最后的结果。
每一次排序都利用上次长度为 2^k-1的字符串的 rank 值,那么长度为 2^k 的字符串就可以用两个长度为 2^k-1 的字符串的排名作为关键字表示,
然后进行基数排序,便得出了长度为 2^k的字符串的 rank 值。以字符串“aabaaaab”为例,整个过程如图所示。
其中 x、y 是表示长度为 2^k的字符串的两个关键字 。

1 int wa[maxn],wb[maxn],wv[maxn],ws[maxn]; 2 int cmp(int *r,int a,int b,int l) { 3 return r[a]==r[b]&&r[a+l]==r[b+l]; 4 } 5 void da(int *r,int *sa,int n,int m) { 6 int i,j,p,*x=wa,*y=wb,*t; 7 for(i=0; i<m; i++) ws[i]=0; 8 for(i=0; i<n; i++) ws[x[i]=r[i]]++; 9 for(i=1; i<m; i++) ws[i]+=ws[i-1]; 10 for(i=n-1; i>=0; i--) sa[--ws[x[i]]]=i; 11 for(j=1,p=1; p<n; j*=2,m=p) { 12 for(p=0,i=n-j; i<n; i++) y[p++]=i; 13 for(i=0; i<n; i++) if(sa[i]>=j) y[p++]=sa[i]-j; 14 for(i=0; i<n; i++) wv[i]=x[y[i]]; 15 for(i=0; i<m; i++) ws[i]=0; 16 for(i=0; i<n; i++) ws[wv[i]]++; 17 for(i=1; i<m; i++) ws[i]+=ws[i-1]; 18 for(i=n-1; i>=0; i--) sa[--ws[wv[i]]]=y[i]; 19 for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1; i<n; i++) 20 x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; 21 } 22 }
待排序的字符串放在 r 数组中,从 r[0]到 r[n-1],长度为 n,且最大值小于 m。为了函数操作的方便,约定除 r[n-1]外所有的 r[i]都大于 0, r[n-1]=0。
函数结束后,结果放在 sa 数组中,从 sa[0]到 sa[n-1]。
函数的第一步,要对长度为 1 的字符串进行排序。
一般来说,在字符串的题目中,r 的最大值不会很大,所以这里使用了基数排序。如果 r 的最大值很大,那么把这段代码改成快速排序。
代码:
1 for(i=0;i<m;i++) ws[i]=0; 2 for(i=0;i<n;i++) ws[x[i]=r[i]]++; 3 for(i=1;i<m;i++) ws[i]+=ws[i-1]; 4 for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;
这里 x 数组保存的值相当于是 rank 值。
下面的操作只是用 x 数组来比较字符的大小,所以没有必要求出当前真实的 rank 值。
接下来进行若干次基数排序,在实现的时候,这里有一个小优化。
基数排序要分两次,第一次是对第二关键字排序,第二次是对第一关键字排序。
对第二关键字排序的结果实际上可以利用上一次求得的 sa 直接算出,没有必要再算一次。
代码:
1 for(p=0,i=n-j;i<n;i++) y[p++]=i; 2 for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
其中变量j是当前字符串的长度,数组y保存的是对第二关键字排序的结果 。
然后要对第一关键字进行排序,代码:
1 for(i=0;i<n;i++) wv[i]=x[y[i]]; 2 for(i=0;i<m;i++) ws[i]=0; 3 for(i=0;i<n;i++) ws[wv[i]]++; 4 for(i=1;i<m;i++) ws[i]+=ws[i-1]; 5 for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];
这样便求出了新的 sa 值。在求出 sa 后,下一步是计算 rank 值。
这里要注意的是,可能有多个字符串的 rank 值是相同的,所以必须比较两个字符串是否完全相同, y 数组的值已经没有必要保存,为了节省空间,这里用 y 数组保存 rank值。
这里又有一个小优化,将 x 和 y 定义为指针类型,复制整个数组的操作可以用交换指针的值代替,不必将数组中值一个一个的复制。
代码:
1 for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++) 2 x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
其中 cmp 函数的代码是:
1 int cmp(int *r,int a,int b,int l) 2 {return r[a]==r[b]&&r[a+l]==r[b+l];}
这里可以看到规定 r[n-1]=0 的好处,如果 r[a]=r[b],说明以 r[a]或 r[b]开头的长度为l的字符串肯定不包括字符r[n-1],所以调用变量r[a+l]和r[b+l]不会导致数组下标越界,这样就不需要做特殊判断。
执行完上面的代码后,rank值保存在 x 数组中,而变量 p 的结果实际上就是不同的字符串的个数。
这里可以加一个小优化,如果 p 等于 n,那么函数可以结束。
因为在当前长度的字符串中 ,已经没有相同的字符串,接下来的排序不会改变 rank 值。
例如图中的第四次排序,实际上是没有必要的。
对上面的两段代码,循环的初始赋值和终止条件可以这样写:
1 for(j=1,p=1;p<n;j*=2,m=p) {…………}
在第一次排序以后,rank 数组中的最大值小于 p,所以让 m=p。
整个倍增算法基本写好,代码大约 25 行。
算法分析:
倍增算法的时间复杂度比较容易分析。每次基数排序的时间复杂度为 O(n),
排序的次数决定于最长公共子串的长度,最坏情况下,排序次数为 logn 次,所以总的时间复杂度为 O(nlogn)。
定义 height[i]=suffix(sa[i-1])和 suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀。
对于同一个后缀,与他排得越近的后缀的最长公共前缀一定更长。
对于height[]数组的计算,我们并不能顺序递推。需要充分利用字符串之间的联系,改变他的计算顺序。
我们定义h[i]: h[i] = height[rank[i]]
即suffix(i)与排名在它前一位的后缀的最长公共前缀长度。
h[i]有一个重要性质:h[i] >= h[i-1] - 1,所以 suffix(i) 和在它前一名的后缀的最长公共前缀至少是h[i-1]-1。
按照从h[1],h[2],……,h[n]的顺序计算h,并利用h数组的性质,复杂度可以降为O(n)。

1 int rank[maxn],height[maxn]; 2 void calheight(int *r,int *sa,int n) { 3 int i,j,k=0; 4 for(i=1; i<=n; i++) rank[sa[i]]=i; 5 for(i=0; i<n; height[rank[i++]]=k) 6 for(k?k--:0,j=sa[rank[i]-1]; r[i+k]==r[j+k]; k++); 7 return; 8 }
LCP(Longest Common Prefix),定义:LCP(j, k)=后缀 j 与后缀 k 的最长公共前缀长度。
那么对于 j 和 k,不妨设rank[j]<rank[k],则有以下性质:
suffix(j) 和 suffix(k) 的 最 长 公 共 前 缀 为 height[rank[j]+1],height[rank[j]+2], height[rank[j]+3], … ,height[rank[k]]中的最小值。
例如,字符串为“aabaaaab”,求后缀“abaaaab”和后缀“aaab”的最长公共前缀,如图所示:
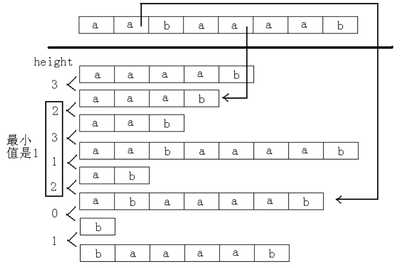
因此求两个后缀的最长公共前缀可以转化为求某个区间上的最小值。
对于这个 RMQ 问题,可以用 ST 算法对 height 数组做 O(nlogn) 的预处理,用 O(1) 的复杂度进行查询。
1、double_algorithm 构造后缀数组;。。。。。O(nlogn)
2、线性计算出h[]数组,再逐个推出height[i];。。。O(n)
3、ST算法对height[]做预处理;。。。。。。。O(nlogn)
4、查询LCP(I,J)只需查询height[rank[i]…rank[j]]中的最小值 O(1)
给定一个字符串,询问某两个后缀的最长公共前缀。
对 height 数组做 RMQ 即可。
一个回文串是指满足如下性质的字符串u:
u[i]=u[len(u)-i+1],对所有的1≤i≤len(u)。
也就是说,回文串u是关于u的中间位置“对称”的。
按照回文串的长度的奇偶性把回文串分为两类:长度为奇数的回文串称为奇回文串,长度为偶数的回文串称为偶回文串。
给定一个字符串,求最长回文子串。
算法分析:
穷举每一位,然后计算以这个字符为中心的最长回文子串。
注意这里要分两种情况,一是回文子串的长度为奇数,二是长度为偶数。
两种情况都可以转化为求一个后缀和一个反过来写的后缀的最长公共前缀。
具体的做法是:将整个字符串反过来写在原字符串后面,中间用一个特殊的字符隔开。
这样就把问题变为了求这个新的字符串的某两个后缀的最长公共前缀。
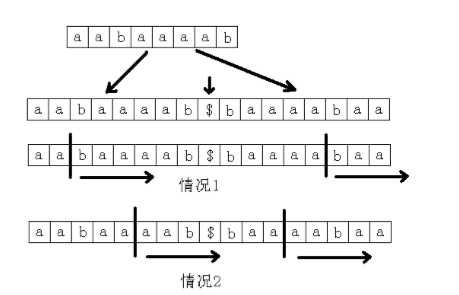
给定两个字符串 A 和 B,求最长公共子串。
算法分析:
字符串的任何一个子串都是这个字符串的某个后缀的前缀。
求 A 和 B 的最长公共子串等价于求 A 的后缀和 B 的后缀的最长公共前缀的最大值。
如果枚举 A和 B 的所有的后缀,那么这样做显然效率低下。
由于要计算 A 的后缀和 B 的后缀的最长公共前缀,所以先将第二个字符串写在第一个字符串后面,中间用一个没有出现过的字符隔开,再求这个新的字符串的后缀数组。
观察一下,看看能不能从这个新的字符串的后缀数组中找到一些规律。以 A=“aaaba”,B=“abaa”为例,如图所示。
那么是不是所有的 height 值中的最大值就是答案呢?
不一定!有可能这两个后缀是在同一个字符串中的,所以实际上只有当 suffix(sa[i-1])和suffix(sa[i])不是同一个字符串中的两个后缀时,height[i]才是满足条件的。
而这其中的最大值就是答案。记字符串 A 和字符串 B 的长度分别为|A|和|B|。
求新的字符串的后缀数组和 height 数组的时间是 O(|A|+|B|),然后求排名相邻但原来不在同一个字符串中的两个后缀的 height 值的最大值,时间也是O(|A|+|B|),
所以整个做法的时间复杂度为 O(|A|+|B|)。时间复杂度已经取到下限,由此看出,这是一个非常优秀的算法。
给定一个字符串,求不相同的子串的个数。
算法分析:
每个子串一定是某个后缀的前缀,那么原问题等价于求所有后缀之间的不相同的前缀的个数。
如果所有的后缀按照 suffix(sa[1]), suffix(sa[2]),suffix(sa[3]), …… ,suffix(sa[n])的顺序计算,不难发现,对于每一次新加进来的后缀 suffix(sa[k]),它将产生 n-sa[k]+1 个新的前缀。
但是其中有height[k]个是和前面的字符串的前缀是相同的。
所以 suffix(sa[k])将“贡献”出 n-sa[k]+1- height[k]个不同的子串。累加后便是原问题的答案。
这个做法的时间复杂度为 O(n)。
原文:http://www.cnblogs.com/zinthos/p/3899725.html