张恭庆编《泛函分析讲义》第一章第4节 线性赋范空间习题解答

1.范数的例子

 在二维空间 $\bbR^2$ 中, 对每一点 $z=(x,y)$ , 令

$$\bex \sen{z}_1=\sev{x}+\sev{y};\quad \sen{z}_2=\sqrt{x^2+y^2}; \eex$$ $$\bex \sen{z}_3=\max\sex{\sev{x},\sev{y}};\quad \sen{z}_4=\sex{x^4+y^4}^\frac{1}{4}. \eex$$

(1) 求证 $\sen{\cdot}_i(i=1,2,3,4)$ 都是 $\bbR^2$ 的范数.

(2) 画出 $(\bbR^2,\sen{\cdot}_i)(i=1,2,3,4)$ 各空间中的单位球面图形.

(3) 在 $\bbR^2$ 中取定三点 $O=(0,0),\ A=(1,0),\ B=(0,1)$ , 试在上述四种不同范数下求出 $\triangle OAB$ 三边的长度.

证明:

(1)由 $Minkowski$ 不等式易知 $\sen{\cdot}_i(i=1,2,3,4)$ 都是 $\bbR^2$ 的范数.

(2)如图

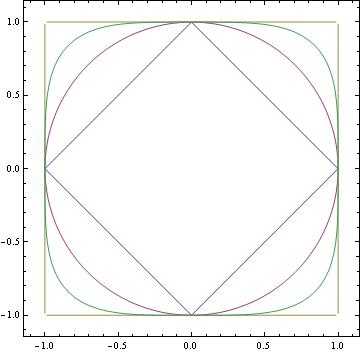
(3)

$$\bex \sen{OA}_1=\sen{OB}_1=1,\quad \sen{AB}_1=2; \eex$$ $$\bex \sen{OA}_2=\sen{OB}_2=1,\quad \sen{AB}_2=\sqrt{2}; \eex$$ $$\bex \sen{OA}_3=\sen{OB}_3=1,\quad \sen{AB}_3=1; \eex$$ $$\bex \sen{OA}_4=\sen{OB}_4=1,\quad \sen{AB}_4=\sqrt[4]{2}; \eex$$ 注记: 图的 Mathematica 代码为

ContourPlot[ {Abs[x] + Abs[y] - 1, Sqrt[x^2 + y^2] - 1, Max[Abs[x], Abs[y]] - 1, (x^4 + y^4)^(1/4) - 1 }, {x, -1.1, 1.1}, {y, -1.1, 1.1} ]

 

 

2. $l^\infty\subset BC(0,1]$

 设 $BC(0,1]$ 表示 $(0,1]$ 上连续且有界的函数 $x(t)$ 全体. 对 $\forall\ x\in BC(0,1]$ , 令 $\dps{\sen{x}=\sup_{0\leq t\leq 1}\sev{x(t)}}$ . 求证:

(1) $\sen{\cdot}$ 是 $BC(0,1]$ 空间上的范数.

(2) $l^\infty$ 与 $BC(0,1]$ 的一个子空间是等距同构的.

证明:

(1)显然.

(2)构造 $BC(0,1]$ 的子集

$$\bex M=\sed{x\in BC(0,1];\ x \mbox{ 在 } \sex{\frac{1}{i+1},\frac{1}{i}}(i\in\bbN)\mbox{ 为直线段}}, \eex$$ 则易知 $M$ 与 $l^\infty$ 等距同构. 事实上, $x\in M$ 由 $\dps{\sed{x\sex{\frac{1}{i}}}_{i=1}^\infty\in l^\infty}$ 唯一确定, 且 $$\bex \sen{x}=\sup_{i\in \bbN}\sev{x\sex{\frac{1}{i}}}. \eex$$

 

 

3. $Sobolev$ 空间 $W^{1,1}[0,1]$

 在 $C^1[0,1]$ 中, 令

$$\bex \sen{f}_1=\sez{\int_a^b \sex{\sev{f}^2+\sev{f‘}^2}\rd x }^\frac{1}{2}\quad (f\in C^1[a,b]). \eex$$

(1)求证 $\sen{\cdot}_1$ 是 $C^1[a,b]$ 上的范数.

(2)问 $\sex{C^1[a,b],\sen{\cdot}_1}$ 是否完备?

证明:

(1) 直接演算知 $\sen{\cdot}_1$ 确为 $C^1[a,b]$ 上的范数.

(2)不完备. 事实上, 不妨设 $[a,b]=[-1,1]$ , 则

a. $\dps{f_n(x)=\sqrt{x^2+\frac{1}{n^2}}}$ 是 $\sex{C^1[a,b],\sen{\cdot}_1}$ 的基本列. 这是因为当 $m>n$ 时,

$$\bex & &\sen{f_n-f_m}_1^2\\ &=&2\int_0^1 \sev{\sqrt{x^2+\frac{1}{n^2}}-\sqrt{x^2+\frac{1}{m^2}}}^2\rd x\\ & &+2\int_0^1 x^2\sev{\frac{1}{\sqrt{x^2+\frac{1}{n^2}}} -\frac{1}{\sqrt{x^2+\frac{1}{n^2}}}}^2\rd x\\ &\equiv&I_1+I_2; \eex$$ $$\bex I_1&=&2\int_0^1 \sex{ \frac{1}{n^2}+\frac{1}{m^2} +2x^2-2\sqrt{x^2+\frac{1}{n^2}} \sqrt{x^2+\frac{1}{m^2}} }\rd x\\ &\leq&\frac{4}{n^2}\to 0 \quad (n\to \infty), \eex$$ $$\bex I_2 &=&2\int_0^1 \frac{x^2}{\sex{x^2+\frac{1}{n^2}}\sex{x^2+\frac{1}{m^2}}} \sez{\sqrt{x^2+\frac{1}{n^2}}-\sqrt{x^2+\frac{1}{m^2}}}^2\rd x\\ &\leq&2\int_0^1 \frac{\sex{\frac{1}{n^2}-\frac{1}{m^2}}^2}{ \sex{\sqrt{x^2+\frac{1}{n^2}}+\sqrt{x^2+\frac{1}{m^2}}}^2 }\rd x\\ &\leq&\frac{2}{n^4}\int_0^1 \frac{1}{x^2+\frac{1}{n^2}}\rd x =\frac{2}{n^3}\int_0^1 \frac{1}{1+(nx)^2}\rd(nx)\\ &=&\frac{2}{n^3}\arctan n\\ &\to&0\quad (n\to \infty). \eex$$

b. $f_n$ 按范数 $\sen{\cdot}_1$ 收敛到 $f(x)=\sev{x}\not\in C^1[a,b]$ . 这是因为

$$\bex \sen{f_n-f}_1^2 &=&2\int_0^1 \sev{\sqrt{x^2+\frac{1}{n^2}}-x}^2\rd x +2\int_0^1 \sev{\frac{x}{x^2+\frac{1}{n^2}}-1}^2\rd x\\ &=&2\int_0^1 \sex{2x^2+\frac{1}{n^2}-2x\sqrt{x^2+\frac{1}{n^2}}}\rd x\\ & &+2\int_0^1 \sez{ \sex{1-\frac{\frac{1}{n^2}}{x^2+\frac{1}{n^2}}} -\frac{2x}{\sqrt{x^2+\frac{1}{n^2}}} +1 }\rd x\\ &=&2\sez{\frac{2}{3}+\frac{1}{n^2}-\frac{2}{3}\sex{1+\frac{1}{n^2}}^\frac{3}{2}+\frac{2}{3n^3}}\\ & &+2\sez{1-\frac{\arctan n}{n}-2\sqrt{1+\frac{1}{n^2}}+\frac{2}{n}+1}\\ &\to&0\quad (n\to\infty). \eex$$

注记: 其实 $C^1[a,b]$ 按模

$$\bex \sen{f}_1=\sez{\int_a^b \sex{\sev{f}^2+\sev{f‘}^2}\rd x }^\frac{1}{2}\quad (f\in C^1[a,b]). \eex$$ 下的完备化空间为 $W^{1,2}[a,b]=H^1[a,b]$ .

 

 

4.等价范数的例子

 在 $C[0,1]$ 中, 对每一个 $f\in C[0,1]$ , 令

$$\bex \sen{f}_1=\sex{\int_0^1 \sev{f(x)}^2\rd x}^\frac{1}{2},\quad \sen{f}_2=\sex{\int_0^1 (1+x)\sev{f(x)}^2\rd x}^\frac{1}{2}. \eex$$ 求证: $\sen{\cdot}_1$ 和 $\sen{\cdot}_2$ 是 $C[0,1]$ 中的两个等价范数.

证明: 易知 $\sen{\cdot_1}_1$ 与 $\sen{\cdot}_2$ 均为 $C[0,1]$ 中的范数. 注意到, 对 $f\in C[0,1]$ ,

$$\bex \sen{f}_1\leq \sen{f}_2; \eex$$ $$\bex & &\sen{f}_2^2 =\int_0^1 (1+x)\sev{f(x)}^2\rd x \leq 2\int_0^1 \sev{f(x)}^2\rd x =2\sen{f}_1^2\\ &\ra&\sen{f}_2\leq \sqrt{2}\sen{f}_1. \eex$$ 我们有题中所述结论.

 

 

5.范数不等价的例子

 设 $BC[0,\infty)$ 表示 $[0,\infty)$ 上连续且有界的函数 $f(x)$ 全体, 对于每个 $f\in BC[0,\infty)$ 及 $a>0$ , 定义

$$\bex \sen{f}_a =\sex{\int_0^\infty e^{-ax}\sev{f(x)}^2\rd x}^\frac{1}{2}. \eex$$

(1)求证: $\sen{\cdot}_a$ 是 $BC[0,\infty)$ 上的范数.

(2)若 $a,b>0,\ a\neq b$ . 求证 $\sen{\cdot}_a$ 与 $\sen{\cdot}_b$ 作为 $BC[0,\infty)$ 上的范数是不等价的.

证明:

(1)由 $Minkowski$ 不等式易知 $\sen{\cdot}_a$ 确为 $BC[0,\infty)$ 上的范数.

(2)设 $b>a>0$ , 则对 $f\in BC[0,\infty)$ 有 $\sen{f}_b\leq \sen{f}_a$ . 故为证两范数不等价, 仅须找一列 $\sed{\sen{f_n}}_{n=1}^\infty\subset BC[0,\infty)$ 使

$$\bex \frac{\sen{f_n}_b}{\sen{f_n}_a}\to 0. \eex$$ 事实上, 取 $$\bex f_n(x)=\left\{\ba{lll} e^{ax},&0\leq x\leq n,\\ e^{an}(n+1-x),&n\leq x\leq n+1,\\ 0,&x\geq n+1. \ea\right. \eex$$ 则有 $$\bex \sen{f_n}_b\leq \int_0^\infty e^{-bx}e^{ax}\rd x=\frac{1}{b-a}, \eex$$ $$\bex \sen{f_n}_a\geq \int_0^n e^{-ax}e^{ax}\rd x=n. \eex$$

 

 

6.乘积 $B$ 空间

 设 $\scrX_1,\scrX_2$ 是两个 $B^*$ 空间, $x_1\in\scrX_1$ 和 $x_2\in \scrX_2$ 的序对 $(x_1,x_2)$ 全体构成空间 $\scrX=\scrX_1\times \scrX_2$ , 并赋以范数

$$\bex \sen{x}=\max\sed{\sen{x_1}_1,\sen{x_2}_2}, \eex$$ 其中 $x=(x_1,x_2)$ , $x_1\in \scrX_1$ , $x_2\in \scrX_2$ , $\sen{\cdot}_1$ 和 $\sen{\cdot}_2$ 分别是 $\scrX_1$ 和 $\scrX_2$ 的范数. 求证: 如果 $\scrX_1,\ \scrX_2$ 是 $B$ 空间, 那么 $\scrX$ 也是 $B$ 空间.

证明: 这是显然的, $\scrX$ 中列的收敛等价于按坐标收敛.

 

 

7. $B^*$ 空间完备的一充要条件

 设 $\scrX$ 是 $B^*$ 空间. 求证: $\scrX$ 是 $B$ 空间, 必须且仅须

$$\bex \forall\ \sed{x_n}\subset \scrX,\ \sum_{n=1}^\infty\sen{x_n}<\infty\ra \sum_{n=1}^\infty x_n\mbox{ 收敛}. \eex$$

证明: $\ra$ 设 $X$ 是 $B$ 空间, $\sed{x_n}_{n=1}^\infty\subset \scrX$ 满足 $\dps{\sum_{n=1}^\infty \sen{x_n}<\infty}$ , 则由

$$\bex m>n\ra \sen{\sum_{k=n+1}^m x_k} \leq \sum_{k=n+1}^m \sen{x_k} \eex$$ 知 $\dps{\sed{\sum_{k=1}^n x_k}_{n=1}^\infty}$ 为基本列, 而 $\dps{\sum_{n=1}^\infty x_n}$ 收敛. $\la$ 设 $\sed{x_n}\subset\scrX$ 为基本列, 则 $$\bex \mbox{对 }\ve=\frac{1}{2},\ \exists\ n_1\in\bbN,\ s.t.\ n\geq n_1\ra \sen{x_n-x_{n_1}}\leq \frac{1}{2}, \eex$$ $$\bex \mbox{对 }\ve=\frac{1}{2^2},\ \exists\ n_2\geq n_1,\ s.t.\ n\geq n_2\ra \sen{x_n-x_{n_2}}\leq \frac{1}{2^2}, \eex$$ $$\bex \cdots \eex$$ $$\bex \mbox{对 }\ve=\frac{1}{2^k},\ \exists\ n_k\geq n_{k-1},\ s.t.\ n\geq n_k\ra \sen{x_n-x_{n_k}}\leq \frac{1}{2^k}, \eex$$ $$\bex \cdots \eex$$ 这样, $$\bex \sum_{k=1}^\infty \sen{x_{n_{k+1}}-x_{n_k}}\leq \sum_{k=1}^\infty\frac{1}{2^k}<\infty. \eex$$ 于是 $\dps{\sum_{k=1}^\infty \sex{x_{n_{k+1}}-x_{n_k}}}$ 收敛, 即有 $\sed{x_{n_k}}_{k=1}^\infty$ 收敛. 由题 第1章第2节第2题 知 $\sed{x_n}_{n=1}^\infty$ 收敛.

 

 

8. $C[a,b]$ 到次数 $\leq n$ 的多项式组成的空间的投影

 记 $[a,b]$ 上次数不超过 $n$ 的多项式全体为 $\bbP_n$ . 求证: $\forall\ f\in C[a,b],\ \exists\ P_0\in \bbP_n$ , 使得

$$\bex \max_{a\leq x\leq b}\sev{f(x)-P_0(x)} =\min_{P\in \bbP_n} \max_{a\leq x\leq b}\sev{f(x)-P(x)}. \eex$$ 也就是说, 如果用所有次数不超过 $n$ 的多项式去对 $f(x)$ 一致逼近, 那么 $P_0(x)$ 是最佳的.

证明: 用 $C[a,b]$ 表示 $[a,b]$ 上所有连续函数 $f(x)$ 的全体, 赋以范数 $\dps{\sen{f}=\max_{a\leq x\leq b}\sev{f(x)}}$ 而成为 $B$ 空间. 此时,

$$\bex \bbP_n=span\sed{1,x,x^2,\cdots,x^n}. \eex$$ 题要证的即是 $$\bex \forall\ f\in C[a,b],\ \exists\ P_0\in \bbP_n,\ s.t.\ \sen{f-P_0}=\min_{P\in\bbP_0}\sen{f-P}. \eex$$ 而这恰为定理 $1.4.23$ 的结论.

 

 

9.最佳逼近元不唯一的例子

 在 $\bbR^2$ 中, 对 $\forall\ x=(x_1,x_2)\in \bbR^2$ , 定义范数

$$\bex \sen{x}=\max\sed{\sev{x_1},\sev{x_2}}. \eex$$ 并设 $e_1=(1,0)$ , $x_0=(0,1)$ . 求 $a\in \bbR^1$ 适合 $$\bex \sen{x_0-ae_1}=\min_{\lambda\in \bbR^1}\sen{x_0-\lambda e_1}. \eex$$ 并问这样的 $a$ 是否唯一? 请对结果作出几何解释.

证明: 由

$$\bex \sen{x_0-\lambda e_1} =\sen{(-\lambda,1)} =\max\sed{\sev{\lambda},1} =\left\{\ba{ll} 1,&\sev{\lambda}\leq 1,\\ \sev{\lambda},&\sev{\lambda}>1, \ea\right. \eex$$ 知 $$\bex \min_{\lambda\in \bbR^1}\sen{x_0-\lambda e_1} =1=\sed{\sen{x_0-ae_1};\ \sev{a}=1}. \eex$$ 这就说明了最佳逼近元的不唯一性. 几何解释如下: $\bbR^2$ 的范数 $\sen{\cdot}$ 不是严格凸的, 其单位球面为正方形, 同一条边上任意两点之连线仍位于单位球面上.

 

 

10.严格凸的等价定义

 求证范数的严格凸性等价于下列条件:

$$\bex \sen{x+y}=\sen{x}+\sen{y}\ \sex{\forall\ x\neq 0,\ y\neq 0}\ \ra\ x=cy\ (c>0). \eex$$

证明: 回忆: $B^*$ 空间中范数 $\sen{\cdot}$ 是严格凸的, 是指

$$\bex \sen{x}=1=\sen{y},\ x\neq y,\ \alpha\in (0,1) \ \ra\ \sen{\alpha x+(1-\alpha)y}<1. \eex$$ 往证等价性. $\ra$ 设 $x\neq 0$ , $y\neq 0$ 满足 $x\neq cy$ , $\forall\ c>0$ . 往证 $$\bex \sen{x+y}<\sen{x}+\sen{y}. \eex$$ 不妨设 $\sen{x}<\sen{y}$ . 记 $\dps{\tilde x=\frac{\sen{y}}{\sen{x}}x\neq y}$ , 则 $\sen{\tilde x}=\sen{y}$ . 于是 $$\bex \sen{x+y} &=&\sen{ \frac{\sen{x}}{\sen{y}}\tilde x +\sex{1-\frac{\sen{x}}{\sen{y}}}y +\frac{\sen{x}}{\sen{y}}y}\\ &\leq&\sen{ \frac{\sen{x}}{\sen{y}}\tilde x +\sex{1-\frac{\sen{x}}{\sen{y}}}y}+\sen{x}\\ &<&\sez{ \sen{x} +\sex{1-\frac{\sen{x}}{\sen{y}}}\sen{y}} +\sen{x}\\ &=&\sen{x}+\sen{y}. \eex$$ $\la$ 设 $\sen{x}=1=\sen{y}$ , $x\neq y$ , $\alpha\in (0,1)$ , 则 $$\bex c>0\ra \alpha x\neq c(1-\alpha)y, \eex$$ 而 $$\bex \sen{\alpha x+(1-\alpha)y} <\sen{\alpha x}+\sen{(1-\alpha)y} =\alpha\cdot 1+(1-\alpha)\cdot 1 =1. \eex$$ 注记: $\ra$ 另证如下. 设 $x\neq 0$ , $y\neq 0$ 适合 $\sen{x+y}=\sen{x}+\sen{y}$ , 则 $$\bee \sen{\frac{\sen{x}}{\sen{x}+\sen{y}}\cdot\frac{x}{\sen{x}} +\frac{\sen{y}}{\sen{x}+\sen{y}}\cdot\frac{y}{\sen{y}}}=1. \eee$$ 往证 $\dps{\frac{x}{\sen{x}}=\frac{y}{\sen{y}}}$ . 用反证法. 若 $\dps{\frac{x}{\sen{x}}\neq\frac{y}{\sen{y}}}$ , 则由范数的严格凸性, $\eqref{1.4.10:eq}$ 之左端 $<1$ . 这是一个矛盾. 故 $\dps{x=\frac{\sen{x}}{\sen{y}}y}$ .

 

 

11.凸函数的性质

 设 $\scrX$ 是线性赋范空间, 函数 $\varphi:\scrX\to \bbR^1$ 称为凸的, 如果不等式

$$\bex \varphi(\lambda x+(1-\lambda)y) \leq \lambda \varphi(x) +(1-\lambda)\varphi(y)\quad (\forall\ 0\leq \lambda \leq 1) \eex$$ 成立. 求证凸函数的局部极小值必然是全空间最小值.

证明: 设 $x_0\in \scrX$ 是凸函数 $\varphi:\scrX\to \bbR^1$ 的局部极小值, 则对 $\forall\ x\in \scrX$ , 取 $\lambda\in (0,1)$ 充分接近 $1$ , 使

$$\bex \varphi(x_0)\leq \varphi(\lambda x_0+(1-\lambda)x) \leq \lambda \varphi(x_0)+(1-\lambda)\varphi(x), \eex$$ 而 $$\bex \varphi(x_0)\leq \varphi(x). \eex$$

 

 

12.到有限维子空间的最佳逼近元

 设 $\sex{\scrX,\sen{\cdot}}$ 是一线性赋范空间, $M$ 是 $\scrX$ 的有限维子空间, $\sed{e_1,e_2,\cdots,e_n}$ 是 $M$ 的一组基. 给定 $g\in \scrX$ , 引进函数 $F:\bbK^n\to \bbR^1$ . 对 $\forall\ c=(c_1,c_2,\cdots,c_n)\in\bbK^n$ , 规定

$$\bex F(c)=F(c_1,c_2,\cdots,c_n)= \sen{\sum_{i=1}^nc_ie_i-g}. \eex$$

(1)求证 $F$ 是一个凸函数.

(2)若 $F(c)$ 的最小值点是 $c=(c_1,c_2,\cdots,c_n)$ . 求证

$$\bex f=\sum_{i=1}^nc_ie_i \eex$$ 给出了 $g$ 在 $M$ 中的最佳逼近元.

证明:

(1) 对 $\forall\ p=(p_1,p_2,\cdots,p_n)\in \bbK^n$ , $q=(q_1,q_2,\cdots,q_n)\in \bbK^n$ , $\forall\ \lambda \in [0,1]$ , 有

$$\bex F\sex{\lambda p+(1-\lambda) q} &=&\sen{\sum_{i=1}^n \sez{\lambda p_i+(1-\lambda)q_i}e_i-g}\\ &=&\sen{\lambda \sex{\sum_{i=1}^np_ie_i-g} +(1-\lambda)\sex{\sum_{i=1}^nq_ie_i-g}}\\ &\leq&\lambda \sen{\sum_{i=1}^n p_ie_i-g} +(1-\lambda) \sen{\sum_{i=1}^n q_ie_i-g}\\ &=&\lambda F(p)+(1-\lambda)F(q). \eex$$

(2)按定义,

$$\bex \sen{\sum_{i=1}^n c_ie_i-g} =F(c) =\min_{d\in \bbK^n}F(d) =\min_{d\in \bbK^n}\sen{\sum_{i=1}^n d_ie_i-g}, \eex$$ 即 $\dps{f=\sum_{i=1}^nc_ie_i}$ 为 $g$ 在 $M$ 中的最佳逼近元. 注记: 由题 第1章第4节第11题 及 第1章第4节第12题 知, 有了最佳逼近元旦存在唯一性后, 其计算方法可化归为求一凸函数的极小值.

 

 

13.线性子空间稠密的一充分条件

 设 $\scrX$ 是 $B^*$ 空间, $\scrX_0$ 是 $\scrX$ 的线性子空间, 假定 $\exists\ c\in (0,1)$ , 使得

$$\bex \inf_{x\in \scrX_0}\sen{y-x}\leq c\sen{y}\quad (\forall\ y\in \scrX). \eex$$ 求证: $\scrX_0$ 在 $\scrX$ 中稠密.

证明: 若 $\overline{\scrX_0}\neq \scrX$ , 则由 $Riesz$ 引理,

$$\bex \exists\ y\in \scrX:\ \sen{y}=1,\ s.t.\ \rho(y,\overline{\scrX_0})>c. \eex$$ 但按条件, $$\bex \rho(y,\overline{\scrX_0})\leq \rho(y,\scrX_0)\leq c. \eex$$ 这是一个矛盾. 故有 $\overline{\scrX_0} = \scrX$ 。

 

 

14. $C_0$ 中最佳逼近元不存在的例子

 设 $C_0$ 表示以 $0$ 为极限的实数列全体, 并在 $C_0$ 中赋以范数

$$\bex \sen{x}=\max_{n\geq 1}\sev{\xi_n}\quad \sex{\forall\ x=(\xi_1,\xi_2,\cdots,\xi_n,\cdots)\in C_0}. \eex$$ 又设 $$\bex M=\sed{x=\sed{\xi_n}_{n=1}^\infty\in C_0;\ \sum_{n=1}^\infty \frac{\xi_n}{2^n}=0}. \eex$$

(1)求证: $M$ 是 $C_0$ 的闭子空间.

(2)设 $x_0=(2,0,\cdots,0,\cdots)$ . 求证:

$$\bex \inf_{z\in M}\sen{x_0-z}=1. \eex$$ 但 $\forall\ y\in M$ 有 $\sen{x_0-y}>1$ .

证明:

(1) 设

$$\bex M\ni x^k=\sed{\xi^k_n}_{n=1}^\infty \to x=\sed{\xi_n}_{n=1}^\infty, \eex$$ 则 $$\bex \lim_{k\to\infty}\sup_{n\in\bbN}\sev{\xi^k_n-\xi_n}=0. \eex$$ 于是 $\forall\ \ve>0,\ \exists\ K\in \bbN$ , s.t. $$\bex & &\sup_{n\bbN}\sev{\xi^K_n-\xi_n}<\ve\\ &\ra& \sev{\sum_{n=1}^\infty\frac{\xi_n}{2}} =\sev{\sum_{n=1}^\infty\frac{\xi_n-\xi_n^K}{2}} \leq \sup_{n\in\bbN}\sev{\xi^K_n-\xi_n}\cdot\sum_{n=1}^\infty\frac{1}{2^n}<\ve. \eex$$ 由 $\ve$ 的任意性有 $\dps{\sum_{n=1}^\infty\frac{\xi_n}{2^n}=0}$ . 这就说明了 $x\in M$ .

(2)记

$$\bex x^k=( \underbrace{1-\frac{1}{2^{k-1}},-1,\cdots,-1} _{k\mbox{ 个}},0,\cdots)\in M, \eex$$ 则 $$\bex \sen{x^k-x_0}=1+\frac{1}{2^{k-1}}\to 1 \quad (k\to\infty). \eex$$ 于是 $$\bex \rho(x_0,M)\leq 1. \eex$$ 往证 $\forall\ y\in M$ , $\sen{x_0-y}>1$ , 从而 $\rho(x_0,M)=1$ . 用反证法. 若 $$\bex \exists\ y=\sed{\eta_n}_{n=1}^\infty \in M,\ s.t.\ \sen{x_0-y}\leq 1, \eex$$ 则 $$\bex 1\geq \sen{x_0-y}=\max\sed{\sev{2-\eta_1},\sup_{n\geq 2}\sev{\eta_n}}, \eex$$ 即 $$\bex 1\leq \eta_1\leq 3,\quad -1\leq \eta_n\leq 1\ (n\geq 2). \eex$$ 但 $\dps{\sum_{n=1}^\infty \frac{\eta_n}{2^n}=0}$ 蕴含(由 $\dps{\lim_{n\to\infty}\eta_n\to 0}$ ) $$\bex \sev{\frac{\eta_1}{2}} =\sev{-\sum_{n=2}^\infty \frac{\eta_n}{2^n}} <\sum_{n=1}^\infty \frac{1}{2^n} =\frac{1}{2}. \eex$$ 这是一个矛盾. 故有结论. 注记: 本题提供一个例子说明: 对于无穷维闭线性子空间来说, 给定其外一点 $x_0$ , 未必能在其上找到一点 $y$ 适合 $$\bex \sen{x_0-y}=\inf_{z\in M}\sen{x_0-z}. \eex$$ 换句话说, 给定 $x_0\not\in M$ , 未必能在 $M$ 中找到最佳逼近元.

 

 

15.到有限维真子空间的最佳逼近元的存在性

 设 $\scrX$ 是 $B^*$ 空间, $M$ 是 $\scrX$ 的有限维真子空间. 求证: $\exists\ y\in \scrX:\ \sen{y}=1$ , 使得

$$\bex \sen{y-x}\geq 1\quad (\forall\ x\in M). \eex$$

证明: 设 $y_0\not\in M$ , 则 $d=\rho(y_0,M)>0$ , 按定义,

$$\bex \forall\ n\in\bbN,\ \exists\ x_n\in M,\ s.t.\ d\leq \sen{x_n-y_0}<d+\frac{1}{n}. \eex$$ 由于 $\dim M<\infty$ , 而 $\sed{x_n}_{n=1}^\infty$ 有子列 $x_{n_k}\to x_0\in M$ . 这蕴含 $\sen{y_0-x_0}=d$ . 记 $$\bex y=\frac{y_0-x_0}{\sen{y_0-x_0}}, \eex$$ 则 $\sen{y}=1$ 且 $$\bex x\in M\ra \sen{y-x}=\frac{\sen{y_0-\sex{x_0+\sen{y_0-x_0}x}}}{\sen{y_0-x_0}} \geq \frac{d}{d}=1. \eex$$

 

 

16. $Lipschitz$ 空间

 若 $f$ 是定义在区间 $[0,1]$ 上的复值函数, 定义

$$\bex \omega_\delta(f) =\sup\sed{\sev{f(x)-f(y)};\ \forall\ x,y\in [0,1],\ \sev{x-y}<\delta}. \eex$$ 如果 $0<\alpha\leq 1$ 对应的 $Lipschitz$ 空间 $Lip\ \alpha$ , 由满足 $$\bex \sen{f}=\sev{f(0)}+\sup_{\delta>0}\sed{\delta^{-\alpha}\omega_\delta(f)}<\infty \eex$$ 的一切 $f$ 组成, 并以 $\sen{f}$ 为模. 又设 $$\bex lip\ \alpha=\sed{f\in Lip\alpha;\ \lim_{\delta\to 0}\delta^{-\alpha}\omega_\delta(f)=0}. \eex$$ 求证 $Lip\ \alpha$ 是 $B$ 空间, 而且 $lip\ \alpha$ 是 $Lip\ \alpha$ 的闭子空间.

证明:

(1) $Lip\ \alpha$ 是 $B$ 空间. 设 $\sed{f_n}_{n=1}^\infty\subset Lip\ \alpha$ 为基本列, 则

$$\bex \exists\ M>0,\ s.t.\ n\in\bbN\ra \sen{f_n}\leq M. \eex$$ 于是 $\sed{f_n}_{n=1}^\infty\subset C[0,1]$ 是一致有界(为 $M$ )且等度连续 ( $\forall\ \ve>0,\ \exists\ \delta=(\ve/M)^{1/\alpha}>0,\ s.t.\ \cdots$ ). 由 $Ascoli-Arzela$ 定理, $\sed{f_n}_{n=1}^\infty$ 有子列 $\sed{f_{n_k}}_{k=1}^\infty$ 一致收敛到某个 $f\in C[0,1]$ . 于 $$\bex & &\sev{f_n(0)-f_{n_k}(0)}\\ & &+\sup_{\delta>0}\sed{\delta^{-\alpha} \sup_{\sev{x-y}<\delta}\sev{\sex{f_n(x)-f_{n_k}(x)} -\sex{f_n(y)-f_{n_k}(y)}}}<\ve\\ & &(n,k\mbox{ 充分大}) \eex$$ 中令 $k\to\infty$ 有 $\sen{f_n-f}\to 0\ (n\to\infty)$ . 再于 $$\bex \sev{f_n(0)}+\sup_{\delta>0} \sed{\delta^{-\alpha} \sup_{\sev{y-x}<\delta}\sev{f_n(x)-f_n(y)}} \leq M \eex$$ 中令 $n\to\infty$ 有 $\sen{f}\leq M$ , 而 $f\in Lip\ \alpha$ .

(2) $lip\ \alpha$ 是 $Lip\ \alpha$ 的闭子空间. 设 $lip\ \alpha\ni f_n\to f$ , 则对 $\forall\ \ve>0$ , 由

$$\bex \delta^{-\alpha}\omega_\delta(f) \leq \delta^{-\alpha}\omega_\delta(f-f_N) +\delta^{-\alpha}\omega_\delta(f_N) \equiv I_1+I_2 \eex$$ 知可先选取一 $N\in\bbN$ 使 $I_1<\ve/2$ ; 再对该 $N$ , 取 $\delta$ 小使 $I_2<\ve/2$ . 这样, $$\bex \lim_{\delta\to 0} \delta^{-\alpha}\omega_\delta(f)=0, \eex$$ 即 $f\in lip\ \alpha$ .

 

 

17.商空间

 设 $\scrX$ 是赋范线性空间, $\scrX_0$ 是 $\scrX$ 的闭线性子空间, 将 $\scrX$ 中的向量分类, 凡是适合 $x‘-x‘‘\in \scrX_0$ 的两个向量 $x‘,x‘‘(\in\scrX)$ 归于同一类, 称其为等价类. 把一个等价类看成一个新的向量, 这种向量的全体组成的集合用 $\scrX/\scrX_0$ 表示,并称其为商空间. 下列是关于商空间的命题.

(1) 设 $\sez{x}\in\scrX/\scrX_0$ , $x\in \scrX$ . 求证: $z\in\sez{x}$ 的充分且必要条件是 $\sez{x}=z+\scrX_0$ .

(2) 在 $\scrX/\scrX_0$ 中定义加法与数乘如下:

$$\bex \sez{x}+\sez{y}=x+y+\scrX_0\quad \sex{\forall\ \sez{x},\sez{y}\in \scrX/\scrX_0}; \eex$$ $$\bex \lambda \sez{x}=\lambda x+\scrX_0\quad \sex{\forall\ \sez{x}\in\scrX/\scrX_0,\ \forall\ \lambda\in \bbK}, \eex$$ 其中 $x$ 和 $y$ 分别是属于等价类 $\sez{x}$ 和 $\sez{y}$ 的任意元素. 又规定范数 $$\bex \sen{\sez{x}}_0=\inf_{w\in \sez{x}}\sen{w}\quad (\forall\ \sez{x}\in\scrX/\scrX_0). \eex$$ 求证: $\sex{\scrX/\scrX_0,\sen{\cdot}_0}$ 是一个 $B^*$ 空间.

(3) 设 $\sez{x}\in \scrX/\scrX_0$ . 求证对 $\forall\ x\in \sez{x}$ , 有

$$\bex \inf_{z\in \scrX_0}\sen{x-z}=\sen{\sez{x}}_0. \eex$$

(4) 定义映射 $\varphi:\scrX\to \scrX/\scrX_0$ 为

$$\bex \varphi(x)=\sez{x}=x+\scrX_0\quad (\forall\ x\in \scrX). \eex$$ 求证 $\varphi$ 是线性连续映射.

(5) $\forall\ \sez{x}\in \scrX/\scrX_0$ , 求证 $\exists\ x\in \scrX$ , 使得

$$\bex \varphi(x)=\sez{x},\mbox{ 且 } \sen{x}\leq 2\sen{\sez{x}}_0. \eex$$

(6) 设 $\sex{\scrX,\sen{\cdot}}$ 完备. 求证 $\sex{\scrX/\scrX_0,\sen{\cdot}_0}$ 也是完备的.

(7) 设 $\scrX=C[0,1]$ , $\scrX_0=\sed{f\in \scrX;\ f(0)=0}$ . 求证:

$$\bex \scrX/\scrX_0 \cong \bbK, \eex$$ 其中记号 $\cong$ 表示等距同构.

证明:

(1) $\ra$ 注意到

$$\bex & &z\in \sez{x}\\ &\ra&z-x\in \scrX_0\\ &\ra&\forall\ w\in \sez{x},\ w=z+\sez{(x-z)+(w-x)}\in z+\scrX_0\\ &\ra& \sez{x}\subset z+\scrX_0, \eex$$ 及 $$\bex z+\scrX_0=x+\sez{(z-x)+\scrX_0}\subset x+\scrX_0. \eex$$ $\la$ 易知 $x\in \sez{x}$ , 而 $$\bex x=z+w,\ w\in \scrX_0, \eex$$ $$\bex z-x=w\in \scrX_0, \eex$$ $$\bex z\in \sez{x}. \eex$$

(2) 易知加法与数乘运算是定义合理的. 为证结论, 只要验证

$$\bex \sen{\sez{x}}_0=0\ra \sez{x}=0\lra x\in \scrX_0. \eex$$ 事实上, 按定义, $$\bex \forall\ n\in\bbN,\ \exists\ x_n\in\sez{x},\ s.t.\ \sen{x_n}<\frac{1}{n}. \eex$$ 而 $$\bex \scrX_0\ni x_n-x\to -x. \eex$$ 由 $\scrX_0$ 的闭性知 $x\in \scrX_0$ .

(3)一方面, 按定义,

$$\bex \forall\ \ve>0,\ \exists\ z_0\in \scrX_0,\ s.t.\ \sen{x-z_0}<\inf_{z\in \sez{x_0}}\sen{x-z}+\ve. \eex$$ 再由 $$\bex x-z_0\in x+\scrX_0=\sez{x} \eex$$ 知 $$\bex \sen{\sez{x}}_0=\inf_{w\in \sez{x}}\sen{w} \leq \sen{x-z_0} <\inf_{z\in \sez{x_0}}\sen{x-z}+\ve. \eex$$ 由 $\ve$ 的任意性有 $$\bex \sen{\sez{x}}_0\leq \inf_{z\in \sez{x_0}}\sen{x-z}. \eex$$ 另一方面, 同样按照定义, $$\bex \forall\ \ve>0,\ \exists\ w_0\in\sez{x},\ s.t.\ \sen{w_0}<\inf_{w\in\sez{x}}\sen{w}+\ve. \eex$$ 注意到 $$\bex w_0\in \sez{x}\ra x-w_0\in\scrX_0, \eex$$ 我们有 $$\bex \inf_{z\in \scrX_0}\sen{x-z}\leq \sen{x-\sex{x-w_0}} =\sen{w_0}<\inf_{w\in\sez{x}}\sen{w}+\ve. \eex$$ 又由 $\ve$ 的任意性, 最终得到结论.

(4)商空间 $\scrX/\scrX_0$ 上的加法与数乘运算保证了 $\varphi$ 是线性的. 又由

$$\bex \sen{\varphi(x)}_0 =\sen{\sez{x}}_0 =\inf_{w\in \sez{x}}\sen{w} \leq \sen{x} \eex$$ 知 $\varphi$ 是连续的.

(5) $\forall\ \sez{x}\in \scrX/\scrX_0$ , 若 $\sez{x}=0$ , 则

$$\bex \exists\ z=0,\ s.t.\ \varphi(z)=\sez{x}\mbox{ 且 } \sen{z}=0=2\sen{\sez{x}}_0. \eex$$ 不然, $\sen{\sez{x}}_0>0$ , 而由下确界定义, $$\bex \exists\ z\in \sez{x},\ s.t.\ \sen{z}\leq 2\sen{\sez{x}}_0. \eex$$ 这时, 由 (1) 知 $\varphi(z)=z+\scrX_0=\sez{x}$ .

(6)设 $\sed{\sez{x_n}}_{n=1}^\infty\subset \scrX/\scrX_0$ 为基本列, 则有一子列 $\sed{\sez{x_{n_k}}}_{k=1}^\infty$ 使

$$\bex \sum_{k=1}^\infty \sen{\sez{x_{n_{k+1}}-x_{n_k}}}_0<\infty. \eex$$ 由 (5)知 $$\bex \exists\ y_{n_k}\in \sez{x_{n_{k+1}}-x_{n_k}},\ s.t.\ \sen{y_{n_k}}\leq 2\sen{\sez{x_{n_{k+1}}-x_{n_k}}}_0. \eex$$ 利用第1章第4节第7题 知 $\dps{\sum_{k=1}^\infty y_{n_k}=x\in \scrX}$ , 且有 $$\bex \sez{x} &=&\varphi(x)\\ &=&\varphi\sex{\sum_{k=1}^\infty y_{n_k}}\\ &=&\sum_{k=1}^\infty\varphi\sex{y_{n_k}}\\ &=&\sum_{k=1}^\infty \sez{x_{n_{k+1}}-x_{n_k}}\\ &=&\lim_{k\to\infty}\sez{x_{n_k}}. \eex$$ 再据第1章第2节第2题, 有 $\sez{x_n}\to \sez{x}\ (n\to\infty)$ .

(7)作映射

$$\bex \ba{cccc} T:&\scrX/\scrX_0&\to&\bbK,\\ &\sez{f}&\mapsto&f(0). \ea \eex$$ 显然 $T$ 是满的. 往证 $$\bex \sev{T\sez{f}}=\sen{\sez{f}}_0. \eex$$ 一方面, $$\bex & &g(x)\equiv T\sez{f}\in \sez{f}\\ &\ra&\sen{\sez{f}}_0\leq \sen{g}=\sev{T\sez{f}}. \eex$$ 另一方面, 按定义, $$\bex \forall\ \ve>0,\ \exists\ g\in \sez{f},\ s.t.\ \sen{g}<\sen{\sez{f}}+\ve. \eex$$ 又于 $$\bex \sen{g}=\max_{x\in [0,1]}\sev{g(x)} \geq \sev{g(0)} =\sev{f(0)} =\sev{T\sez{f}}, \eex$$ 中令 $\ve\to 0^+$ , 有 $$\bex \sev{T\sez{f}}\leq \sen{\sez{f}}_0. \eex$$

张恭庆编《泛函分析讲义》第一章第4节 线性赋范空间习题解答

原文：http://www.cnblogs.com/zhangzujin/p/3548760.html