http://www.cnblogs.com/Konjakmoyu/p/6050343.html
关于扫描线的理解
https://vjudge.net/contest/242515#problem/F
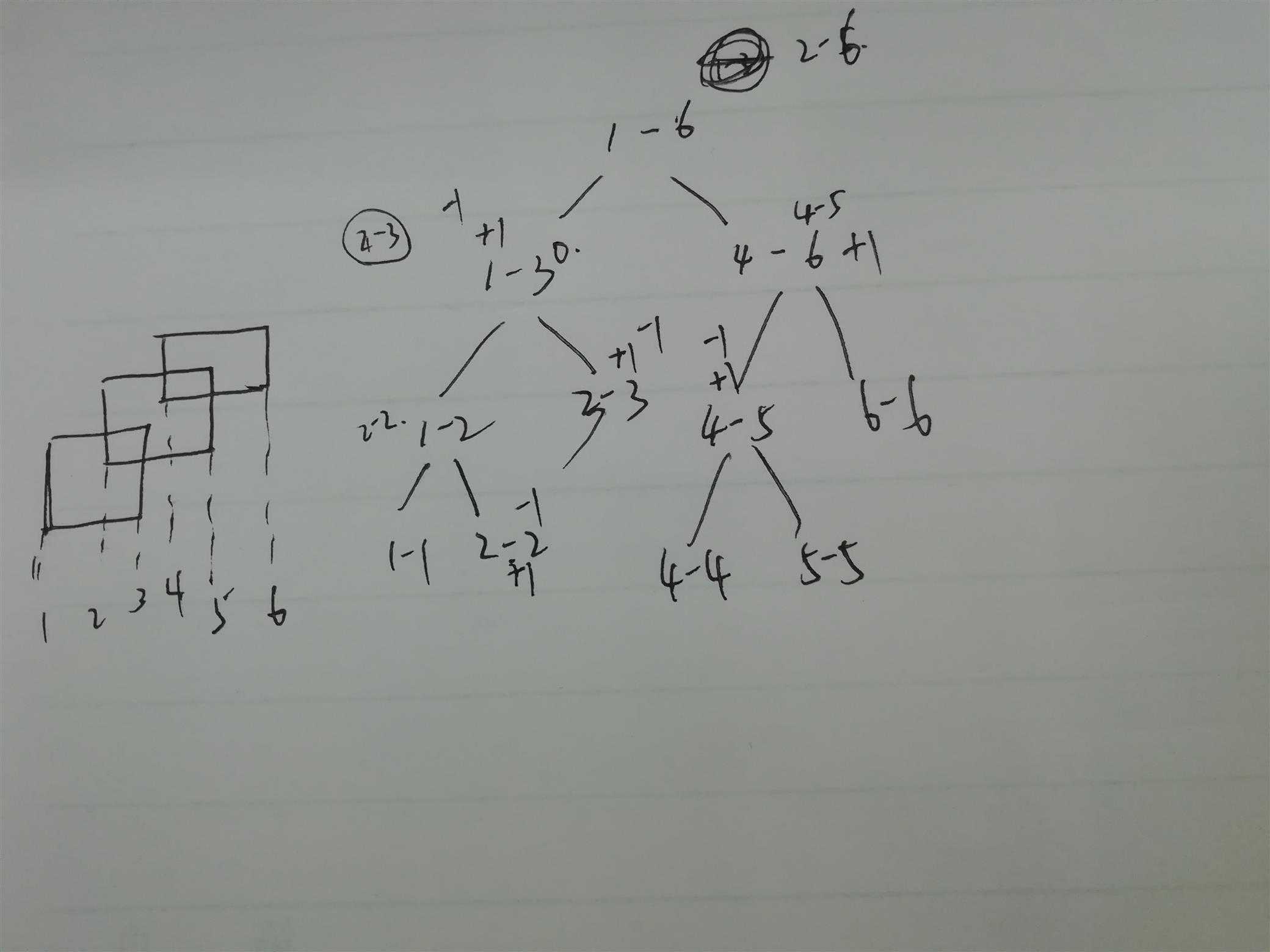
这个题目是求总的矩形覆盖面积。线段树中的点表示的是一段区间的长度。线段按照纵坐标由小到大来更新进线段树。
线段树的结构体中有个lazy标记与长度标记,lazy标记表示这个区间段被覆盖了几次,每次只要更新相对应区间的lazy值,不需要push_down 操作,然后push_up操作是来更新长度值,如果lazy标记为1,则表示该区间
有效,如果是叶子节点就是0,如果是0就表示不能确定,只能有其左右孩子的值来确定,(这里体现为什么不需要push_down操作,因为不一定要递归到叶子节点来找长度,可以直接拿一个已经标记了的区间来表示长度,如果标记为0表示没有被标记过或者先前的1被抵消掉了(在纸上画一下),那么就要通过子节点来得到长度。)
#include<bits/stdc++.h> using namespace std; const int maxm = 105; struct seg { double x1, x2, h; int fl; // seg(double x1 = 0, double x2 = 0, double h = 0, int fl = 0) : x1(x1), x2(x2), h(h), fl(fl) {}; bool operator < (const struct seg &a) const { return h < a.h; } }seg[maxm * 2]; struct Node { int l, r; int mid() { return (l + r) >> 1; } }node[maxm << 3]; int lazy[maxm << 3]; double sum[maxm << 3]; double xx[maxm * 2]; int n; void build(int ri, int l, int r) { node[ri].l = l; node[ri].r = r; lazy[ri] = 0; sum[ri] = 0; if(l == r) return; int m = node[ri].mid(); build(ri << 1, l, m); build(ri << 1 | 1, m + 1, r); } void push_up(int ri) { if(lazy[ri]) { sum[ri] = xx[node[ri].r + 1] - xx[node[ri].l ]; return; } if(node[ri].l == node[ri].r) { sum[ri] = 0; return; } sum[ri] = sum[ri << 1] + sum[ri << 1 | 1]; } void update(int ri, int l, int r, int flag) { if(node[ri].l == l && node[ri].r == r) { lazy[ri] += flag; push_up(ri); return; } int m = node[ri].mid(); if(r <= m) update(ri << 1, l, r, flag); else if(l > m) update(ri << 1 | 1, l, r, flag); else { update(ri << 1, l, m, flag); update(ri << 1 | 1, m + 1, r, flag); } push_up(ri); } int main() { double x1, x2, y1, y2; int ca = 0; while(~scanf("%d", &n) && n) { for(int i = 1; i <= n; i++) { scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2); seg[2 * i - 1] = (struct seg) {x1, x2, y1, 1}; xx[2 * i - 1] = x1; seg[2 * i] = (struct seg) {x1, x2, y2, -1}; xx[2 * i] = x2; } sort(seg + 1, seg + 2 * n + 1); sort(xx + 1, xx + 2 * n + 1); int k = unique(xx + 1, xx + 2 * n + 1) - xx; build(1, 1, k - 1); double res = 0; for(int i = 1; i < 2 * n; i++) { int l = lower_bound(xx + 1, xx + k, seg[i].x1) - xx; int r = lower_bound(xx + 1, xx + k, seg[i].x2) - xx - 1; if(l <= r) { // printf("nas\n"); update(1, l, r, seg[i].fl); } res += sum[1] * (seg[i + 1].h - seg[i].h); } // for(int i = 1; i <= 3; i++) printf("%.2f\n", len[i]); printf("Test case #%d\nTotal explored area: %.2f\n\n", ++ca, res); } return 0; }
http://acm.hdu.edu.cn/showproblem.php?pid=1255
求覆盖两次的矩形面积。
https://blog.csdn.net/codeswarrior/article/details/81081692 跟覆盖一次的差不多,只是结构体中长度的变为一个至少覆盖一次与至少覆盖两次的长度。
http://acm.csu.edu.cn:20080/csuoj/problemset/problem?pid=1082
求一个点最多是多少个矩形的交点,然后要如果一个y值有多条线,应该先让正直的先进去,然后再试负值的,保证最小。
#include<map> #include<set> #include<cmath> #include<queue> #include<cstdio> #include<string> #include<vector> #include<cstring> #include<iostream> #include<algorithm> #include<functional> using namespace std; typedef long long LL; typedef pair<int, int> PII; const int MX = 2e4 + 5; #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define root 0,10000,1 int MAX[MX << 2], col[MX << 2]; struct Que { int L, R, top, d; bool operator<(const Que &b)const { if(top == b.top) return d > b.d; return top < b.top; } Que(int _top = 0, int _L = 0, int _R = 0, int _d = 0) { L = _L; R = _R; top = _top; d = _d; } } Q[MX]; void push_up(int rt) { MAX[rt] = max(MAX[rt << 1], MAX[rt << 1 | 1])+ col[rt]; } //void push_down(int rt) { // if(col[rt]) { // col[rt << 1] += col[rt]; // col[rt << 1 | 1] += col[rt]; // MAX[rt << 1] += col[rt]; // MAX[rt << 1 | 1] += col[rt]; // col[rt] = 0; // } //} void update(int L, int R, int d, int l, int r, int rt) { if(L <= l && r <= R) { MAX[rt] += d; col[rt] += d; return; } int m = (l + r) >> 1; // push_down(rt); if(L <= m) update(L, R, d, lson); if(R > m) update(L, R, d, rson); push_up(rt); } int main() { int n; //freopen("input.txt", "r", stdin); while(~scanf("%d", &n)) { memset(MAX, 0, sizeof(MAX)); memset(col, 0, sizeof(col)); for(int i = 1; i <= n; i++) { int x1, x2, y1, y2; scanf("%d%d%d%d", &x1, &x2, &y1, &y2); Q[i] = Que(y1, x1, x2, 1); Q[i + n] = Que(y2, x1, x2, -1); } sort(Q + 1, Q + 1 + 2 * n); int ans = 0; for(int i = 1; i <= 2 * n; i++) { update(Q[i].L, Q[i].R, Q[i].d, root); ans = max(ans, MAX[1]); } printf("%d\n", ans); } return 0; }
https://vjudge.net/contest/285943#status/xiayuyang/N/0/
原文:https://www.cnblogs.com/downrainsun/p/10698391.html