向量运算与几何意义

向量：具有大小与方向的量，在几何中通常用带有箭头的线段表示，代数中通常用上方写有箭头的字母表示\((\vec u)\)

向量相加采取平行四边形法则，意义：沿着\(\vec u\)走后再沿着\(\vec w\)走的终点

推广到一般：\[\begin{aligned}\vec u = \begin{bmatrix}\begin{array}{ccc}x_1 \\y_1 \\\end{array}\end{bmatrix}\vec w = \begin{bmatrix}\begin{array}{ccc}x_2 \\y_2 \\\end{array}\end{bmatrix}\\vec u + \vec w = \vec v = \begin{bmatrix}\begin{array}{ccc}x_1 + x_2 \\y_1 + y_2\\\end{array}\end{bmatrix}\end{aligned}\]

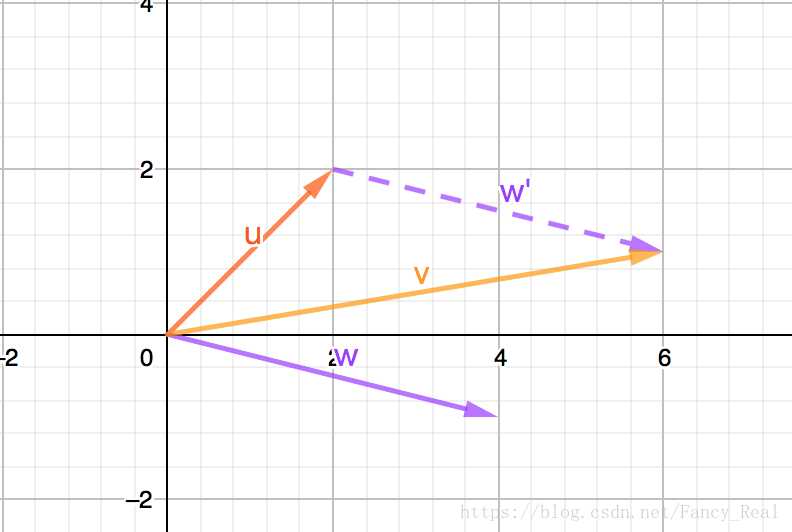
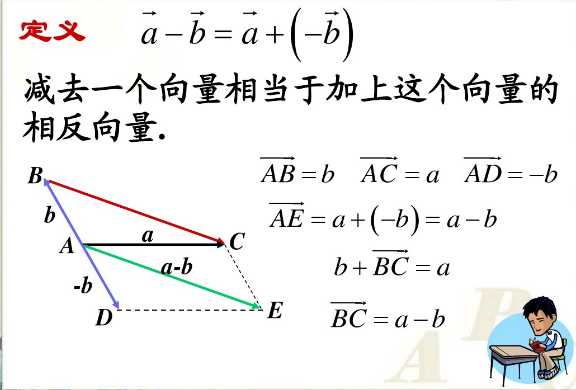
减法

向量叉积

\(a(x_1,y_1),b(x_2,y_2)\Longrightarrow x_1y_2-x_2y_1\)我们通过平移+割补的方法可以证明出这恰好是平行四边形面积

向量运算与几何意义

原文：https://www.cnblogs.com/y2823774827y/p/10334082.html