链表的每个结点有三个域,分别是head,rep,tail
head是个指针,指向这个集合的第一个元素,tail也是个指针,指向这个集合的最后一个元素,rep是某个元素的代表值

如上图所示,这是一个S1∪S2的操作,即将S2的每个结点的head指针都指向S1的第一个元素即f,将S1的每个结点的尾指针都指向S2的最后一个元素即h
这么操作的时间复杂度是\(\theta(n^2)\)
假设我们要合并n个集合,每个集合都刚刚初始化为仅含有1个元素因为合并集合是两两进行合并的,每合并一次都要修改i次头指针或者i次尾指针,(i为二者元素的个数的最大值)即每次合并都要更新i个域,那么进行n-1次合并:
\[\sum^{n-1}_{i=1}i=\theta(n^2)\]
每个链表中的域添加一个length,这样每次都可以将小链表接到大链表的后面
我们先仅仅考虑一个元素:\(x_i\)
一开始的时候它是一个元素,然后它会与另一个只有一个元素的集合合并,这个时候这个集合是两个元素;当它下一次加入到别的集合的时候,他一定是比较小的那个,即另一个集合一定有大于等于两个元素,这就意味着每次合并,集合元素数量针对于小的那个集合一定会翻倍
因此如果最后那个集合有n个集合元素的话,那个集合中每个元素都做了\(lgn\)次合并,那么n个元素就是nlgn,即合并操作花费\(nlgn\)时间
如果进行了m次Make_Set操作,所有的花费时间就是\(\theta(m+nlgn)\)
秩(rank):是一棵树的层数的上界,意思就是这棵树有多少层,秩就是多少
执行Find(x)操作的时候,从x到根节点路径上的元素所组成的集合中的所有元素都指向一个最后找到的那个节点
简单来说就是这条路径上的元素从x开始一直到终点r之前的那个元素在Find(x)之后都指向r,这样就方便了后续的查找
Find操作不改变任何结点的秩

如图所示,Find(a)之前集合是长成左图(a)的样子,Find(a)之后集合就长成了右图(b)的样子
秩依据以下三点进行维护:
1.MakeSet(x)操作执行时定义结点的秩为0(即初始化时结点的秩为0)
2.合并时如果rank(x) = rank(y),那么让x指向y的代表元素,并且y的秩+1
3.合并时如果rank(x) < rank(y),那么rank(y)和rank(x)的秩保持不变,并且让x指向y或者y指向x
注意:以上操作其他结点的秩不发生改变

图中情形a、b分别代表了合并时的两种情况
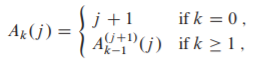
简单说一下这个函数:
对于任何整数j:
\[
\begin{aligned}
A_1(j) &= A_0^{(j+1)}(j)\\&=A_0(A_0(A_0...A_0(j))...) \\&= j+(1+...+1)\\&= 2j+1\\end{aligned}\]
\[
\begin{aligned}
A _2(j) &= A_1^{(j+1)}(j)\\&=A_1(A_1(A_1...A_1(j))...)\\&=2^jA_1(j)+2^{j-1}+...2+1\\&=2^{j+1}(j+1)-1
\\\end{aligned}
\]
\[
\begin{aligned}
A_3(1)&=A_2^{(2)}(1)\\&=A_2(A_2(1))\\&=A_2(7) \\&= 2047\\end{aligned}
\]
\[
\begin{aligned}
A_4(1)&=A_3^{(2)} \\&= A_3(2047)\\&=A_2^{(2048)}(2047)\\&>>A_2(2047)\\&=2^{2048}·2048-1\\&>2^{2048} \\&= 16^{512}\\&>>10^{80}
\end{aligned}\]
因此在宇宙范围之内我们能遇到的数字都不会超过\(A_4(1)\)
定义\(A(k)的逆函数\alpha(n)=min\{k|A_k(1)\ge{n\}}\)
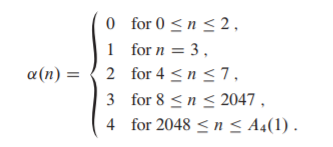
阿克曼函数是严格单调递增的且增长速度非常快,\(A_k(n)>n\)
\(\alpha(n)\)是单调不减的且增长速度缓慢
定义\(x.p\)为指向\(x\)的父节点的指针
显然,x与x的父节点合并之前有两种情况:
1.\(rank(x)=rank(y)\)
合并时\(y=x.p\)且\(rank(y)=rank(y)+1\)
2.\(rank(x)<rank(y)\)
合并时二者的秩不发生改变,\(rank(y)=rank(x.p)\)本身就大于\(rank(x)\)
而显然在这之后x就永远不会作为父结点和别人合并,因此秩不再发生改变,而\(x.p\)可能再作为父结点与别人发生合并或者作为别人的子结点与别人合并之后再也不参与合并
因为每个结点最多合并n-1次,每次秩至多增加1,因此每个结点的秩最大不超过n-1
定义\(\phi_q(x)\)为第q次操作之后并查集森林的势能函数
首先需要定义一个函数:\(level(x) = max\{k|x.p.rank\ge A_k(x.rank)\}\)
level(x)的物理意义是在不超过x的父结点的秩的前提下阿克曼函数最多能作用在x的秩上的"层数",即\(A_k中的k\)
那么我们来看看\(level(x)\)的范围:
由\(level(x)\)的定义可知,\(k\)和\(x.p.rank, x.rank, A(x)\)密切相关,通过寻找\(x.p.rank, x.rank\)之间的关系,结合阿克曼函数的性质,可以得出\(level(x)\)的范围
根据引理2可以得到:\[x.p.rank < n\]
根据\(\alpha(n)\)的定义可以得到:\[n \le A_{\alpha(n)}(1)\]
由\(A_k(n)\)是单调不减的我们可以得到:
\[A_{\alpha(n)}(1)\le A_{\alpha(n)}(x.rank)\]
将上述三式合并:
\[x.p.rank<A_{\alpha(n)}(x.rank)\]
结合\(level(x)\)的定义\(k\)是最大的使得\(x.p.rank\ge A_k(x.rank)\)的整数,我们可以知道\(k\)最大也不会超过\(\alpha(n)\)
因此我们得到\(level(x)\)的范围:\(0\le level(x) < \alpha(n)\)
让我们再来定义另外一个函数:
\[iter(x)=max\{ i|x.p.rank\ge A_{level(x)}^{(i)}(x.rank)\}\]
\(iter(x)\)的物理意义:\(level(x)\)指的是使得\(x.p.rank\ge A_k(x)\)的最大的\(k\),但是我们知道对于相差较大的\(x.p.rank\),我们依然可以得到一样的\(k\),现在这个\(k\)已经求出来了,我们进一步的想要知道阿克曼函数迭代多少次依然能够使得\(x.p.rank\ge A_{level(x)}^{(i)}(x.rank)\),也就是\(iter(x)\), 我个人认为\(iter(x)\)是在\(level(x)\)的基础上对于\(x\)这个结点和它的父结点的秩之间的关系的刻画
那么\(iter(x)\)这个函数的范围是:
根据\(level(x)\)的定义可知:
\[A_{level(x)+1}(x.rank)> x.p.rank\ge A_{level(x)}(x.rank)\]
取等式的左边:
\[x.p.rank<A_{level(x)+1}(x.rank)\]
根据阿克曼函数的定义:
\[A_{level(x)+1}(x.rank) =A_{level(x)}^{(x.rank+1)}(x.rank) \]
即
\[x.p.rank<A_{level(x)}^{(x.rank+1)}(x.rank)\]
结合\(iter(x)\)的定义得:\(iter(x) \le x.rank\)
定义势能函数如下:
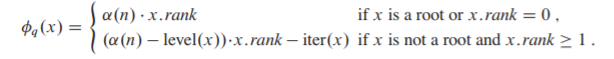
与1相同,应用引理3、4:\[level(x)\ge0,iter(x)\ge1\]
得:
\[
\begin{aligned}
\phi_q(x)&\le(\alpha(n)-0)·x.rank-1\&=\alpha(n)·x.rank-1\&<\alpha(n)·x.rank
\end{aligned}
\]
因此\(0\le \phi_q(x) \le \alpha(n)·x.rank\)
如果 \(level(x)\) 增加,那么它至少增加1,则根据势能函数的定义中的前半部分:
\((\alpha(n)-level(x))·x.rank\)
则\(level(x)\)至少增加1会导致前半部分减少至少\(x.rank\)
而\(level(x)\)的增加可能会导致\(iter(x)\)的减少,但是根据引理4,\(i\le iter(x)<x.rank\), 即\(-iter(x)>-x.rank\)
因此整个势能函数还是减少的,即
\[\phi(x) \le \phi_{q-1}(x)-1\]
MAKE-SET操作会创建一个新的秩为0的结点,所以势能函数大小为0
由于\(y\)在Link之前是根节点,所以\[\phi_{q-1}(y)=\alpha(n)·y.rank\]
Link操作会使得\(y.rank\)不变或者增加1,因此
\[
\begin{aligned}
\phi_q(y)&=\phi_{q-1}(y)\\\phi_q(y)&=(y.rank +1)·\alpha(n)\\&=\phi_{q-1}(y)+\alpha(n)\ \end{aligned}\]
因此\(\phi_{q}(x)+\phi_q(y)-(\phi_{q-1}(x)+\phi_{q-1} (y))\)最多是\(\alpha(n)\)
所以操作的平摊代价是\(O(\alpha(n))\)
不是根节点且在路径上存在一个y使得他们两个的level相等(关于这一点做点说明:如果他们两个的level相等,说明他们的level都处在同一个区间上:\([\alpha(k-1),\alpha(k)),k=1,2,3,...\)反过来看,如果level正好等于\(\alpha(k)\),那么当rank增加的时候,level发生变化的可能性很低,因为\(\alpha(n)\)是一个增加速度很慢的函数,而其他的点即存在另一个点和它自己的level相同的点在rank改变之后很有可能发生改变)
因此我们就有\(\alpha(n)+2\)个结点不满足上述两个条件:根结点和路径最开始的结点(秩等于0)和其他所有level等于\(\alpha(k),k=0,1,2,...\)
然后考虑这些势能函数会发生变化的结点:
令\(k=level(x)=level(y)\)即y是那个路径是与x的level相同的点
在Find之前:
根据\(iter(x)和level(x)的定义:\)
\[
\begin{aligned}
x.p.rank&\ge A_k^{iter(x)}(x.rank)\y.p.rank&\ge A_k(x.p.rank)\\end{aligned}
\]
因为\(y\)是路径上\(x\)之后的结点,由引理1:
\[
\begin{aligned}
y.rank&\ge x.p.rank\\end{aligned}
\]
将这几个式子揉在一起:
\[
\begin{aligned}
y.p.rank &\ge A_k(y.rank)\&\ge A_k(x.p.rank)\&\ge A_k(A_k^{(iter(x))}(x.rank))\&=A_k^{(iter(x)+1)}(x.rank)
\end{aligned}
\]
路径压缩会导致x和y的父结点变成一个人,因此\(x.p.rank=y.p.rank\),而\(x.rank\)没有发生改变,因此\[x.p.rank\ge A_k^{(iter(x)+1)}(x.rank)\]
因此路径压缩会导致\(iter(x)\)至少增加1或者\(level(x)\)至少增加1,根据引理6,可以得到\[\phi_q(x)\le \phi_{q-1}(x)-1\]
也就是说\(x\)的势能函数最少减少1
将实际代价与势能函数变化量相加:
\[
\begin{aligned}
O(s)+(-(s-(\alpha(n)+2)·1)&=O(s)-s+O(\alpha(n))\\&=O(\alpha(n))
\end{aligned}\]
而Union操作可以分解成两个Find操作和一个Link操作
因此对于m个操作(Union和Make-Set)而言,时间复杂度是\(O(m\alpha(n))\)
****
参考文献:
原文:https://www.cnblogs.com/SebastianLiu/p/10701485.html