一.原码和补码
二.memset();
三.ST表
问题:已知n个元素,有m次询问,每次询问[l,r]中的最大值
1.算法一:朴素算法
时间复杂度:
预处理O(n^2);
单次询问O(1);
空间复杂度O(n^2);
2.算法二:线段树
3.算法三:ST表
考虑改进算法一。
f[i][j]表示[i,i+2^j-1]内的最大值
递推边界:显然有[i,i]的最大值为a[i],即f[i][0]=a[i];
现在已知f[l][0],f[l][1],f[l][2] … f[l][n]
显然r会被夹在两个f[][]之间
max[l,r]=max(f[1][2],f[3][2]);
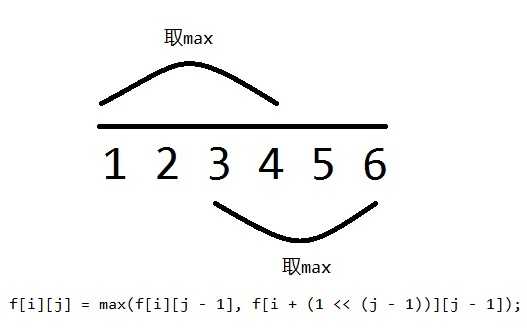
f[i][j]=max(f[i][j-1],f[i+2^(j-1)][j-1]);
1 #include <cstdio> 2 #include <cstring> 3 #include <iostream> 4 #include <cctype> 5 #define rgi register int 6 #define il inline 7 #define ll long long 8 #define maxn 100010 9 10 using namespace std; 11 12 int n, m; 13 int lg2[maxn] = { -1}, a[maxn];//预处理log2,注意log2是关键字,不能用 14 int f[maxn][25]; 15 16 il int read() 17 { 18 rgi x = 0, f = 0, ch; 19 while(!isdigit(ch = getchar())) f |= ch == ‘-‘; 20 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar(); 21 return f ? -x : x; 22 } 23 24 il void write(int x) 25 { 26 if(x < 0) putchar(‘-‘), x = -x; 27 if(x > 9) write(x / 10); 28 putchar(x % 10 + 48); 29 } 30 31 int RMQ(int l, int r) 32 { 33 int len = lg2[r - l + 1]; 34 return max(f[l][len], f[r - (1 << len) + 1][len]);//取两个重叠区间的最大值 35 } 36 37 int main() 38 { 39 n = read(); 40 m = read(); 41 for(rgi i = 1; i <= n; ++i) 42 { 43 lg2[i] = lg2[i >> 1] + 1;//预处理 44 a[i] = read(); 45 f[i][0] = a[i];//递推边界:[i,i]的最大值为a[i] 46 } 47 for(rgi j = 1; j <= lg2[n]; ++j)//先循环j 48 for(rgi i = 1; i + (1 << j) - 1 <= n; ++i) 49 f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]); 50 for(rgi i = 1; i <= m; ++i) 51 { 52 int l = read(), r = read(); 53 write(RMQ(l, r)); 54 putchar(‘\n‘); 55 } 56 return 0; 57 }
原文:https://www.cnblogs.com/Clever-Jimmy/p/ST_table.html