将不是河流的格子染成白色,是河流的格子染成黑色,那么连通块数就是白色格子数$-1*2$的联通白色格子数$-2*1$的联通白色格子数$+2*2$的联通白色格子数。
我们考虑每个格子与它左边、上边、左上三个格子的连通性(同为白色视为联通)。
为了方便起见,对于每个$2*2$的格子,我们将它编号,从左往右、从上往下依次编号为$1,2,3,4$。
我们将$1,2,3$与$4$的连通性都归为$4$号格子对答案的贡献。
显然联通情况有$5$种:$1,2,3,4$、$2,3,4$、$2,4$、$3,4$、$4$。
对于第一种情况,$4$号点对答案的贡献为$1-1-1+1=0$
对于第二种情况,$4$号点对答案的贡献为$1-1-1=-1$
对于第三、四种情况,$4$号点对答案的贡献为$1-1=0$
对于第五种情况,$4$号点对答案的贡献为$1$
可以发现第一、三、四种情况对答案没有影响,而第二、五种情况只会出现在一个连通块的最左边和最上边两排(有一种特殊情况后边再说明)。
对于最左边,如果有一个格子是第二种情况,那么在这个点的同一行的最左边那个点就会是第五种情况,这两个格子的贡献抵消。
对于最上边,如果有一个格子是第二种情况,那么在这个点的同一列的最上边那个点就会是第五种情况,这两个格子的贡献抵消。
但可以发现最左上的那个格子是第五种情况却没有其他格子与它的贡献抵消,所以只有这个格子对这个连通块有贡献。
这样有一个特例就是河流被这个连通块包围起来,即这个连通块是中空的。
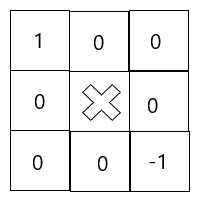
那么右边和下边也会出现第二、五种情况,而对于右下两部分格子中的左上那个格子是第二种情况,会将上面那个对连通块有贡献的格子抵消掉(如下图所示),所以对于这种情况特判一下将答案加一即可。
剩下的就是如何统计上述的四种连通块的个数。
因为地图总大小是$4*10^{10}$,无法对每个点存是否有上述四种贡献。
但可以发现河流的格子最多只有$2*10^5$个格子,我们分别记录哪些格子没有上述四种贡献,然后用总贡献减一下即可。
对于整个地图将横坐标作为版本,对纵坐标建线段树即建立四棵可持久化线段树分别维护上述四种信息。
注意彩虹蛇可能走之前走过的格子,要判重避免重复统计。
#include<set>
#include<map>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<bitset>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
int n,m,q,k;
map<int,int>mp[200010];
int px[200010];
int py[200010];
int tot;
int mx1,mx2,mn1,mn2;
int fx,fy;
int size;
vector<int>t1[200010];
vector<int>t2[200010];
vector<int>t3[200010];
vector<int>t4[200010];
char ch[200010];
int a,b,c,d;
ll ans;
struct lty
{
int cnt;
int root[200010];
int ls[4000010];
int rs[4000010];
int sum[4000010];
void updata(int &rt,int pre,int l,int r,int k)
{
rt=++cnt;
ls[rt]=ls[pre];
rs[rt]=rs[pre];
sum[rt]=sum[pre]+1;
if(l==r)
{
return ;
}
int mid=(l+r)>>1;
if(k<=mid)
{
updata(ls[rt],ls[pre],l,mid,k);
}
else
{
updata(rs[rt],rs[pre],mid+1,r,k);
}
}
int query(int x,int y,int l,int r,int L,int R)
{
if(!y)
{
return 0;
}
if(L<=l&&r<=R)
{
return sum[y]-sum[x];
}
int mid=(l+r)>>1;
int res=0;
if(L<=mid)
{
res+=query(ls[x],ls[y],l,mid,L,R);
}
if(R>mid)
{
res+=query(rs[x],rs[y],mid+1,r,L,R);
}
return res;
}
}tr1,tr2,tr3,tr4;
int main()
{
scanf("%d%d%d%d",&n,&m,&k,&q);
scanf("%d%d",&fx,&fy);
tot++;
px[tot]=fx,py[tot]=fy;
mx1=mn1=fx,mx2=mn2=fy;
mp[fx][fy]=1;
if(k)
{
scanf("%s",ch+1);
}
for(int i=1;i<=k;i++)
{
tot++;
if(ch[i]==‘N‘)
{
fx--;
}
else if(ch[i]==‘S‘)
{
fx++;
}
else if(ch[i]==‘E‘)
{
fy++;
}
else
{
fy--;
}
px[tot]=fx,py[tot]=fy;
mx1=max(mx1,fx);
mn1=min(mn1,fx);
mx2=max(mx2,fy);
mn2=min(mn2,fy);
mp[fx][fy]=1;
}
for(int i=1;i<=tot;i++)
{
int x=px[i],y=py[i];
if(mp[x][y]==2)
{
continue;
}
mp[x][y]=2;
t1[x].push_back(y);
if(y>1)t2[x].push_back(y);
if(y<m&&!mp[x][y+1])t2[x].push_back(y+1);
if(x>1)t3[x].push_back(y);
if(x<n&&!mp[x+1][y])t3[x+1].push_back(y);
if(x>1&&y>1)t4[x].push_back(y);
if(x<n&&y<m&&!mp[x+1][y+1])t4[x+1].push_back(y+1);
if(x<n&&y>1&&!mp[x][y-1]&&!mp[x+1][y])t4[x+1].push_back(y);
if(x>1&&y<m&&!mp[x-1][y]&&!mp[x-1][y+1]&&!mp[x][y+1])t4[x].push_back(y+1);
}
for(int i=1;i<=n;i++)
{
tr1.root[i]=tr1.root[i-1];
tr2.root[i]=tr2.root[i-1];
tr3.root[i]=tr3.root[i-1];
tr4.root[i]=tr4.root[i-1];
size=t1[i].size();
for(int j=0;j<size;j++)
{
tr1.updata(tr1.root[i],tr1.root[i],1,m,t1[i][j]);
}
size=t2[i].size();
for(int j=0;j<size;j++)
{
tr2.updata(tr2.root[i],tr2.root[i],1,m,t2[i][j]);
}
size=t3[i].size();
for(int j=0;j<size;j++)
{
tr3.updata(tr3.root[i],tr3.root[i],1,m,t3[i][j]);
}
size=t4[i].size();
for(int j=0;j<size;j++)
{
tr4.updata(tr4.root[i],tr4.root[i],1,m,t4[i][j]);
}
}
while(q--)
{
scanf("%d%d%d%d",&a,&b,&c,&d);
ans=0;
if(a<mn1&&c>mx1&&b<mn2&&d>mx2)
{
ans++;
}
ans+=1ll*(d-b)*(c-a)-tr1.query(tr1.root[a-1],tr1.root[c],1,m,b,d);
ans-=1ll*(d-b-1)*(c-a)-tr2.query(tr2.root[a-1],tr2.root[c],1,m,b+1,d);
ans-=1ll*(d-b)*(c-a-1)-tr3.query(tr3.root[a],tr3.root[c],1,m,b,d);
ans+=1ll*(d-b-1)*(c-a-1)-tr4.query(tr4.root[a],tr4.root[c],1,m,b+1,d);
printf("%lld\n",ans);
}
return 0;
}
[LOJ2310][APIO2017]斑斓之地——可持久化线段树
原文:https://www.cnblogs.com/Khada-Jhin/p/10703278.html