反向传播算法实质就是链式求导法则的应用,那为什么叫反向传播算法。
前提我们已经熟悉如何求偏导。有下面式子
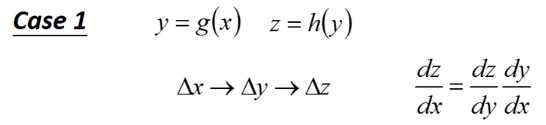
第二个就是链式求导法则,\(\Delta s\)会分别影响\(\Delta x\)与\(\Delta y\)。\(\Delta x\)跟\(\Delta y\)会在会影响\(\Delta z\)。因此\(z\)对\(s\)求偏导就是上面的式子。
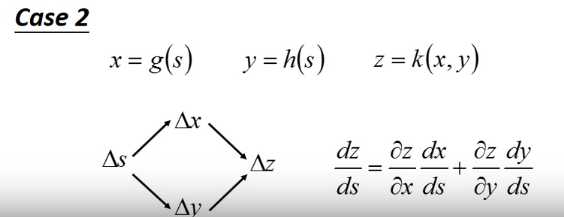
先对一个样本的误差求偏导,则对于任意一个\(w_i\),\(\frac{\partial C}{\partial w}= \frac{\partial z}{\partial w} \frac{\partial C}{\partial z}\) ,当前这里的\(z\)是指当前\(w_i\)直接相关的\(z\),比如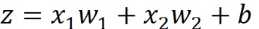 如下图所示。
如下图所示。
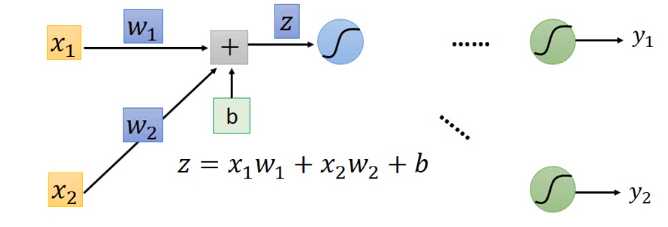
\(\frac{\partial z}{\partial w}\)好求,等于\(x_i\),因为即,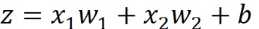 等于与\(w_i\)直接关联的前面的\(x\)的值。如下图
等于与\(w_i\)直接关联的前面的\(x\)的值。如下图
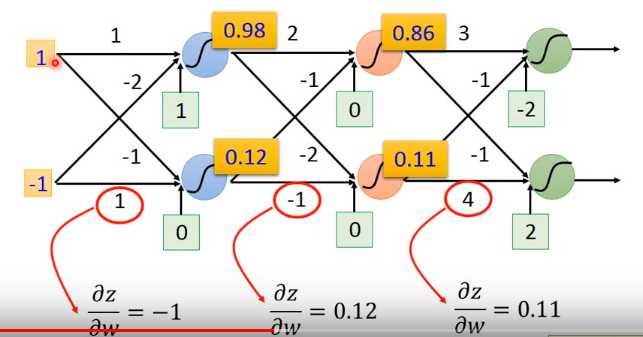
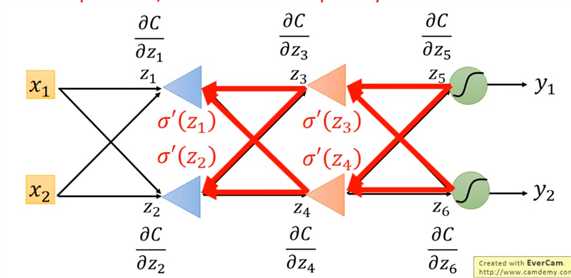
下一步看如何求$ \frac{\partial C}{\partial z}$,假定我们的神经网络结构如下图
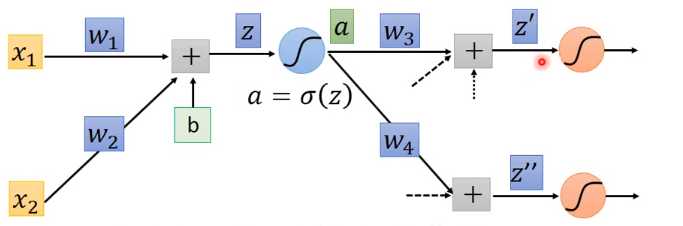
那根据链式求导法则对\(z\)求偏导得到
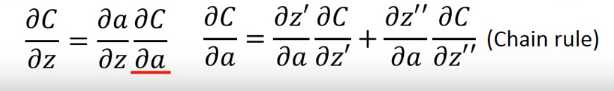
其中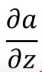 )好求,等于\(\sigma^ {‘}(z)\)即激活函数对\(z\)的导数。而
)好求,等于\(\sigma^ {‘}(z)\)即激活函数对\(z\)的导数。而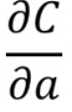 )等于下面
)等于下面
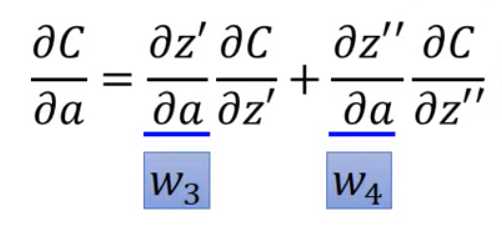
所以如果我们想求出!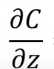 就是求
就是求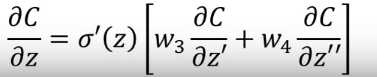 。而求
。而求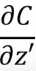 与
与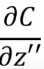 跟求
跟求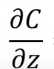 的步骤一模一样,即求与之关联的后面的\(z\)的偏导。如下图
的步骤一模一样,即求与之关联的后面的\(z\)的偏导。如下图
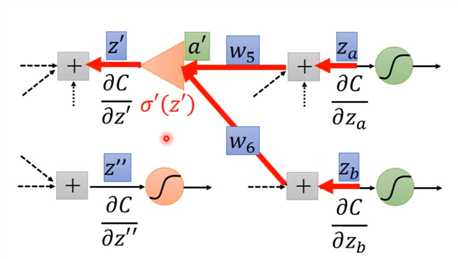
所以每个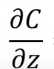 都可以根据后面的
都可以根据后面的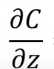 求出,如果我们从最后面开始求
求出,如果我们从最后面开始求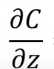 那就可以求出每一步的
那就可以求出每一步的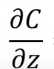 ,在通过\(\frac{\partial C}{\partial w}= \frac{\partial z}{\partial w} \frac{\partial C}{\partial z}\) ,就可以求出每一个\(w_i\) 的偏导数。所以我们称为反向传播算法
,在通过\(\frac{\partial C}{\partial w}= \frac{\partial z}{\partial w} \frac{\partial C}{\partial z}\) ,就可以求出每一个\(w_i\) 的偏导数。所以我们称为反向传播算法
李宏毅 机器学习
原文:https://www.cnblogs.com/lolybj/p/10716055.html