part1
测试:
以多文件结构组织的项目文件示例:在画布上可以上下左右移动的小球
测试效果如下:
part2
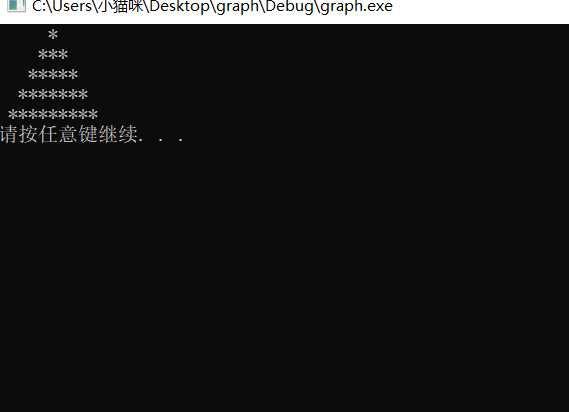
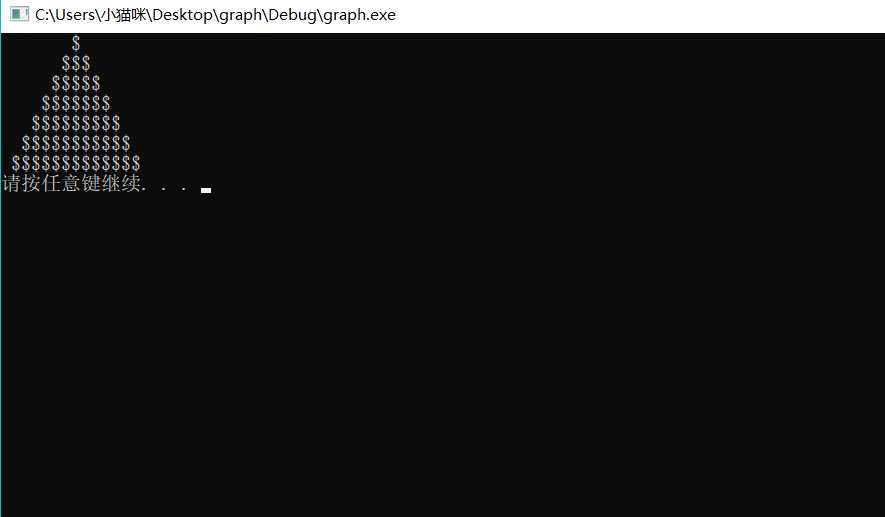
以多文件结构写一个程序,头文件是graph.h,要求输入字符和行数,以一个等腰三角形的形式输出。
代码如下:
//graph.h
#ifndef GRAPH_H #define GRAPH_H // 类Graph的声明 class Graph { public: Graph(char ch, int n); // 带有参数的构造函数 void draw(); // 绘制图形 private: char symbol; int size; }; #endif
//graph.cpp
// 类graph的实现 #include "graph.h" #include <iostream> using namespace std; // 带参数的构造函数的实现 Graph::Graph(char ch, int n) :symbol(ch), size(n) {} // 成员函数draw()的实现 // 功能:绘制size行,显示字符为symbol的指定图形样式 void Graph::draw() { int i, j; for (j = 0; j < size; j++) { for (i = 0; i < size- j; i++) { cout << " "; } for (i = 0; i < (2 * j + 1); i++) { cout << symbol; } cout << endl; } }
//main.cpp
#include <iostream> #include "graph.h" using namespace std; int main() { Graph graph1(‘*‘,5); graph1.draw(); system("pause"); system("cls"); Graph graph2(‘$‘,7); graph2.draw(); system("pause"); return 0; }
实验效果如下:
part3
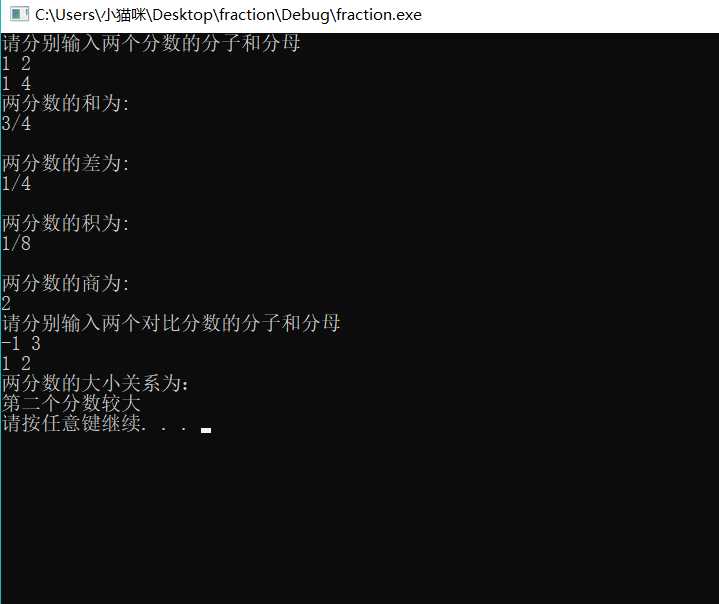
要求以多文件结构写一个程序,要求实现分数之间的加减乘除四则运算以及分数之间大小对比。
//fraction.h
#ifndef FRACTION_H #define FRACTION_H class fraction { public: fraction(int top0 = 0, int bottom0 = 1) :top(top0), bottom(bottom0) {} friend void add(fraction &a, fraction &b); friend void min(fraction &a, fraction &b); friend void mul(fraction &a, fraction &b); friend void div(fraction &a, fraction &b); friend void judge(fraction &a, fraction &b); friend void compare(fraction &a, fraction &b); friend void put(int & top1, int & bottom1); friend void compare(fraction &a, fraction &b); private: int top; int bottom; // 分母 }; #endif
//fraction.cpp
#include"fraction.h" #include<iostream> using namespace std; void judge(fraction &a, fraction &b) { if (a.bottom == 0 || b.bottom == 0) //判断分母是否为零的边缘情况 { if (a.bottom == 0) { cout << "分母不可为零,重新输入第一个分数" << endl; cin >> a.top >> a.bottom; } if (b.bottom == 0) { cout << "分母不可为零,重新输入第二个分数" << endl; cin >> b.top >> b.bottom; } } } void put(int & top1, int & bottom1) //输出函数,包括约分和输出 { int a1, a2; if (top1 > 0 && bottom1 < 0) { top1 = 0-top1; bottom1 = 0-bottom1; } else if (top1 < 0 && bottom1 < 0) { top1 = -top1; bottom1 = -bottom1; } if (top1 > 0) { for (a1=top1; a1 > 1;a1--) { if (top1%a1 == 0) { for (a2 = bottom1; a2 > 1; a2--) { if (bottom1%a2 == 0) { if (a1 == a2) { top1 /= a1; bottom1 /= a2; break; } } } } } } if (top1 < 0) { for (a1 = top1; a1 < 1; a1++) { if (top1 % a1 == 0) { for (a2 = bottom1; a2 > 1; a2++) { if (bottom1%a2 == 0) { if (-a1 == a2) { top1 /= -a1; bottom1 /= a2; break; } } } } } } if (top1 == 0) cout << "0" << endl; else if (bottom1 != 1) cout << top1 << "/" << bottom1 << endl; else cout << top1; } void add(fraction &a, fraction &b) //加法 { int put_top,put_bottom; put_top = a.top*b.bottom + b.top*a.bottom; put_bottom = a.bottom*b.bottom; put(put_top, put_bottom); cout << endl; } void min(fraction &a, fraction &b) //减法 { int put_top, put_bottom; put_top = a.top*b.bottom - b.top*a.bottom; put_bottom = a.bottom*b.bottom; put(put_top, put_bottom); cout << endl; } void mul(fraction &a, fraction &b) //乘法 { int put_top, put_bottom; put_top = a.top*b.top; put_bottom = a.bottom*b.bottom; put(put_top, put_bottom); cout << endl; } void div(fraction &a, fraction &b) //除法 { int put_top, put_bottom; put_top = a.top*b.bottom; put_bottom = a.bottom*b.top; put(put_top, put_bottom); cout << endl; } void compare(fraction &a, fraction &b) //两个分数比大小 { int a1, a2; if (a.top > 0 &&a.bottom < 0) { a.top = 0 - a.top; a.bottom = 0 - a.bottom; } else if (a.top < 0 && a.bottom < 0) { a.top= -a.top; a.bottom = -a.bottom; } if (b.top > 0 && b.bottom < 0) { b.top = 0 - b.top; b.bottom = 0 - b.bottom; } else if (b.top < 0 && b.bottom < 0) { b.top = -b.top; b.bottom = -b.bottom; } if (a.top > 0) { for (a1 = a.top; a1 > 1; a1--) { if (a.top%a1 == 0) { for (a2 =a.bottom; a2 > 1; a2--) { if (a.bottom%a2 == 0) { if (a1 == a2) { a.top /= a1; a.bottom /= a2; break; } } } } } } if (a.top < 0) { for (a1 = a.top; a1 < -1; a1++) { if (a.top% a1 == 0) { for (a2 = a.bottom; a2 > 1; a2++) { if (a.bottom%a2 == 0) { if (-a1 == a2) { a.top/= -a1; a.bottom/= a2; break; } } } } } } if (b.top > 0) { for (a1 = b.top; a1 > 1; a1--) { if (b.top%a1 == 0) { for (a2 = b.bottom; a2 > 1; a2--) { if (b.bottom%a2 == 0) { if (a1 == a2) { b.top /= a1; b.bottom /= a2; break; } } } } } } if (b.top < 0) { for (a1 = a.top; a1 < -1; a1++) { if (b.top% a1 == 0) { for (a2 = b.bottom; a2 > 1; a2++) { if (b.bottom%a2 == 0) { if (-a1 == a2) { b.top /= -a1; b.bottom /= a2; break; } } } } } } //以上都是对两个分数约分 if (a.top == 0&&b.top==0) cout << "两者相等" << endl; else if (a.top==0&&b.top!=0) { cout << "第二个分数较大" << endl; } else if (a.top != 0 && b.top == 0) { cout << "第一个分数较大" << endl; } else if (a.top != 0 && b.top != 0) { if (a.top*b.bottom > a.bottom*b.top) cout << "第一个分数较大" << endl; if (a.top*b.bottom < a.bottom*b.top) cout << "第二个分数较大" << endl; if (a.top*b.bottom ==a.bottom*b.top) cout << "两者相等" << endl; } }
//main.cpp
#include"fraction.h" #include<iostream> #include<cstdlib> using namespace std; int main() { int top1, top2, bottom1, bottom2; int top3, bottom3, top4, bottom4; cout << "请分别输入两个分数的分子和分母" << endl; cin >> top1 >> bottom1; cin >> top2 >> bottom2; fraction a(top1, bottom1); fraction b(top2, bottom2); cout << "两分数的和为:" << endl; add(a, b); cout << "两分数的差为:" << endl; min(a, b); cout << "两分数的积为:" << endl; mul(a, b); cout << "两分数的商为:" << endl; div(a, b); cout << "请分别输入两个对比分数的分子和分母" << endl; cin >> top3 >> bottom3; cin >> top4 >> bottom4; fraction c(top3, bottom3); fraction d(top4, bottom4); cout<<"两分数的大小关系为:"<<endl; compare(c,d); system("pause"); return 0; }
实验反思:
1.关于第一个ball的测试程序,让我更好的弄明白头文件的构造与实现以及与主函数之间的关系。
2.第二个graph的程序,由于在第一个程序中明白了多文件结构的一些注意点,所以这一个实验并没有在结构上耗费太多的时间,主要就是graph.cpp的实现部分了,一开始写的时候理解错了,把它写成一个每行奇数个字符的直角三角形了,然后在纸上画画方格,最后找到了空格和字符的规律。
3.关于第三个实验,改过好几次,第一次想的是定义一个compute类函数,靠识别加减乘除的运算符号来分别计算,写着写着觉得很乱,就推掉重新再来了,第二次是定义了加减乘除四个友元函数,依此计算,但是当时没有再定义一个输出函数,每一个运算函数里都是包括约分、计算、输出,例如加法,先找出两个形参的分母的最小公倍数,然后分别用公倍数除以之前的分母,所得数再乘以分子,以这样的约分化简过程再继续进行加法运算,后来到了输出的时候发现,这样根本就没考虑分母分子为0或者为复数的情况,默认它是整数了,再把这些都实现在一个加法函数里,太过于麻烦繁琐了。于是又推掉重新再来,这次就加减乘除直接运算,加法分子分母交叉相乘相加,把最后的化简全部仍在输出函数里,这样做可以时加减乘除函数看起来明朗很多很多,体现了区块划分,同时也可以放心的把加减乘除函数类型定义成void,不需要再返回值,像第二次尝试的时候时定义成fraction,返回的也是一个分数,这样写的时候就容易出错。
4.两个分数之间的比较函数我写写完后感觉写得很麻烦,两个分数就是先化简再比较,所以化简部分就与输出函数里的化简部分重复了,我就想能否也把比大小放在输出函数里,在化简的同时顺便比个大小,这样就简洁太多太多了,怎么实现呢?就是把compare函数嵌套在输出函数里,然后在main主函数里不需要再额外专门写两个分数比较大小,直接一开始输入的两个分数进行加减乘除,顺便输出大小关系就好了。所以这里可以再改进一下。
原文:https://www.cnblogs.com/21savage-code/p/10720348.html