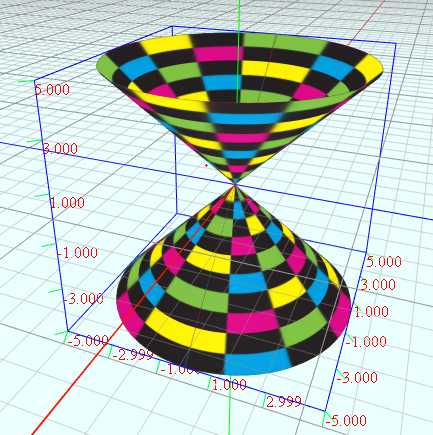
(1)圆锥面
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-5) to (5) dimension2 x = v*cos(u) y = v z = v*sin(u)
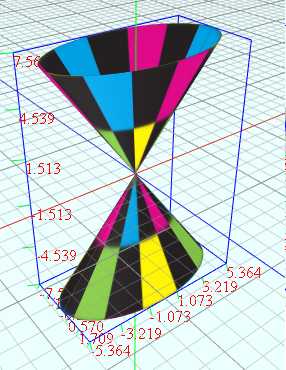
(2)椭圆锥面
#http://www.mathcurve.com/surfaces/coneelliptique/coneelliptique.shtml vertices = D1:100 D2:100 v = from 0 to (2*PI) D1 u = from (-1) to (1) D2 a = rand2(1, 10) b = rand2(1, 10) h = rand2(0.5, 10) x = a*u*cos(v) z = b*u*sin(v) y = h*u
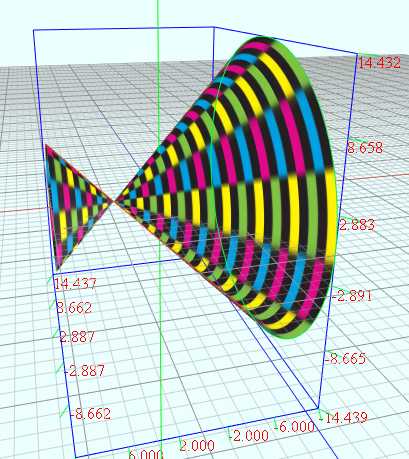
(3)二维直线绕X轴旋转生成圆锥面
vertices = D1:360 D2:100 u = from -10 to 10 D1 v = from 0 to (2*PI) D2 a = rand2(-5, 5) b = rand2(-5, 5) c = rand2(-2, 2) x = u n = c*(x + a) + b y = n*cos(v) z = n*sin(v)
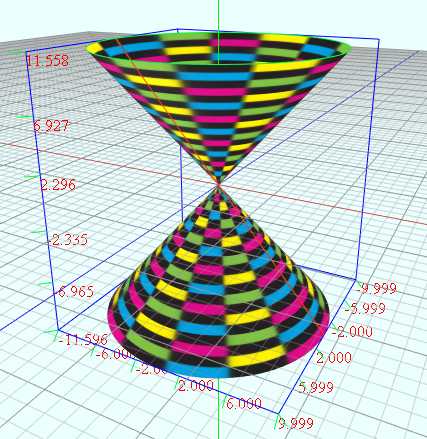
(4)二维直线绕Y轴旋转生成圆锥面
vertices = D1:360 D2:100 u = from -10 to 10 D1 v = from 0 to (2*PI) D2 a = rand2(-5, 5) b = rand2(-5, 5) c = rand2(-2, 2) y = c*(u + a) + b x = u*cos(v) z = u*sin(v)
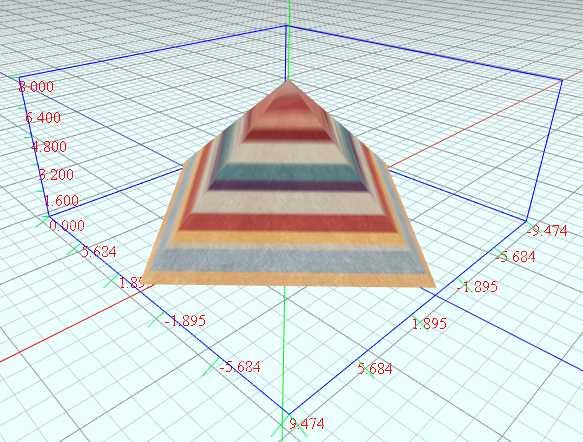
(5)金字塔
vertices = dimension1:5 dimension2:20 u = from 0 to (2*PI) dimension1 v = from 0 to (1) dimension2 r = if (v<0.99, 10, 0) x = r*v*cos(u) z = r*v*sin(u) y = 8*(1-v)
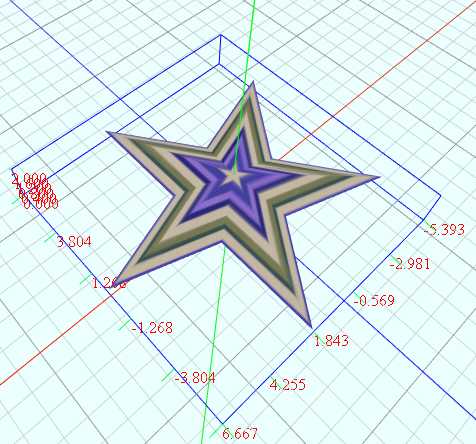
(6)五星
vertices = dimension1:11 dimension2:4 u = from 0 to (2*PI) dimension1 v = from 0 to (1) dimension2 k = from 0 to 10 D1 m = mod(k, 2) t = 10.0 - m*GOLD*10 r = if(v < 0.99, t, 0) x = r*v*cos(u) z = r*v*sin(u) y = 2*(1-v)
(7)N角星
vertices = dimension1:360 dimension2:4 u = from 0 to (2*PI) dimension1 v = from 0 to (1) dimension2 n = rand_int2(4, 32)*2 k = from 0 to (n) D1 m = abs(mod(k, 2) - 1) t = 10.0 - m*GOLD*10 r = if(v < 0.99, t, 0) x = r*v*cos(u) z = r*v*sin(u) y = 2*(1-v)

(8)风车
vertices = dimension1:72 dimension2:4 u = from 0 to (2*PI) dimension1 v = from 0 to (1) dimension2 k = from 0 to 8 D1 m = mod(k, 2) t = 10.0 - m*GOLD*10 r = if(v < 0.99, t, 0) x = r*v*cos(u) z = r*v*sin(u) y = 2*(1-v)

(9)冰淇淋
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from 0 to (PI) dimension2 r = 10.0 x = r*sin(v)*sin(u) y = r*cos(v) z = r*sin(v)*cos(u) a = rand2(PI/2, PI*0.8) d = -r*4 t = r*cos(a) e = (v - a)/(PI - a) w = r*sin(a)*(1 - e) h = t + e*(d - t) i = w*sin(u) j = w*cos(u) x = if(e < 0.0, x, i) y = if(e < 0.0, y, h) z = if(e < 0.0, z, j)

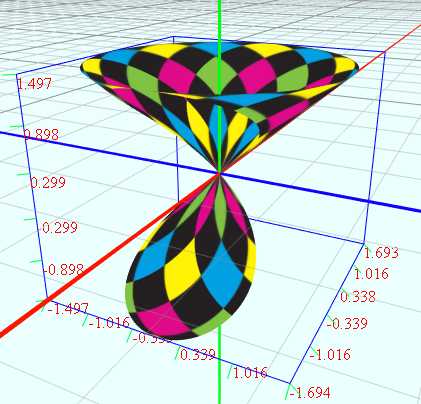
(10)曲线绕Y轴旋转生成圆锥面
#http://www.mathcurve.com/surfaces/conederevolution/conederevolution.shtml vertices = D1:100 D2:100 v = from (-PI) to (PI) D1 u = from (-PI) to (PI) D2 a = rand2(0, PI*0.45) x = a*(cos(v) + cos(u)) z = a*(sin(u) + sin(v)) y = 2*a*cot(a)*cos((u-v)/2)
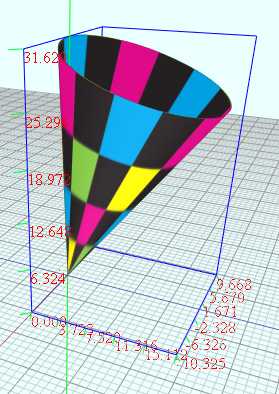
(11)任意朝向的圆锥
vertices = D1:72 D2:72 u = from 0 to (2) D2 v = from 0 to (2*PI) D1 a = rand2(0, 2*PI) b = rand2(0, 2*PI) c = sin(v) d = cos(v) e = sin(b) f = cos(b) g = sin(a) h = cos(a) x = f*h*d - f*g*3 + e*c y = g*d + h*3 z = -e*h*d + e*g*3 + f*c x = x*u y = y*u z = z*u x = x*5 y = y*5 z = z*5
(12)正劈锥体
#http://www.mathcurve.com/surfaces/coinconic/coinconic.shtml vertices = D1:100 D2:100 v = from 0 to (2*PI) D1 u = from -10 to 10 D2 a = rand2(1, 10) b = rand2(1, 10) k = b/a x = u z = k*u*cos(v) y = k*a*sin(v)


原文:http://www.cnblogs.com/iflewless/p/3901130.html