单调栈

单调栈的定义：

单调栈是指一个栈内部的元素是具有严格单调性的一种数据结构，分为单调递增栈和单调递减栈，单调栈只能在栈顶操作。

用拿号排队打个比方：某黑姓小薛拿了一张票，排在一个队列之中，而在他前面的人的号码是递减的，这时小黑就在栈顶，但是小黑不想排队啊，那么他就出去玩了一会，然后再回来排队，但别人也取了票开始排队了，总不能插队吧，那么小黑就从最后一个人的位置（栈顶）开始和排队的人比票号大小，如果小黑的票号比他小，那么小黑很过分的就把他赶出队列（栈顶元素出栈），然后再去跟前面的人比票号，一个个偏历栈内元素直至比到有人票号比他小或者栈为空为止，然后小黑正式在这个位置入栈，小黑的行为看起来很过分（实际上也很过分），但这是为了维护栈的单调性啊，所以非常正义（迫真）。

这个数据结构理解起来很简单，但是使用起来就比较靠电波了

这里放一道单调栈的例题：

Largest Rectangle in a Histogram （http://acm.hdu.edu.cn/showproblem.php?pid=1506)

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:

Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

 

Input

Output

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000
题意：给出一个含有n个矩形的直方图，去求直方图内最大组合矩形的面积

解题思路：

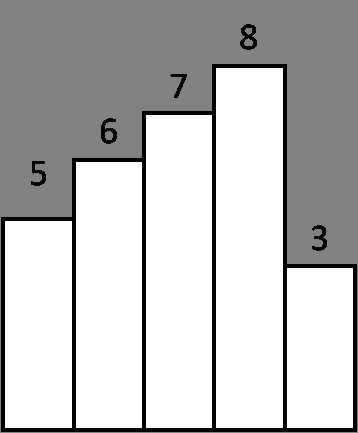比如这个图，h{5,6,7,8,3}，首先一个组合而成的矩形的面积受限于其短板，就是高度最低的直方，我们可以维护一个从栈底到栈顶单调递增栈，将直方的编号而不是高度放入栈，就是先项栈内压入0,1,2,3（直方的编号）,然后当id=4时，h[4]显然小于当前的栈顶元素对应的h，那么将3弹出栈，3作为原来的栈顶，代表着一个峰值，那么弹出过程中可以计算当前栈顶和压入元素的Id差再减一得到中间共有几个直方（包括不在栈内的），既然有可能有不在栈内的，那么直方编号在3,5之间的，这个图中只有一个4，那么矩形大小就是h[4]，但是如果高为7的直方编号为3，但高为8的直方编号为10，那么高为8的直方和高为7的直方中间必然有6个高于8的直方，那么这些直方形成的矩形面积为（3的编号为11-7的编号3-1）*8，像这样递推下去，而当3和5比时，5出栈后栈为空，那么面积就是（3的编号*3），实际上，就是维护一个直方的高度为区间最小值的最大区间长度的积（差点把自己讲晕了，晕了的代码在下面.....）

 1 #include<bits/stdc++.h>
 2 using namespace std;
 3 typedef long long ll;
 4 typedef unsigned long long ull;
 5 #define INF 0x3f3f3f3f
 6 const ll MAXN = 1e5 + 7;
 7 const ll MOD = 1e9 + 7;
 8 const double pi = acos(-1);
 9 ll h[MAXN];
10 int main()
11 {
12     ios::sync_with_stdio(false);    
13     cin.tie(0);
14     cout.tie(0);
15     int n;
16     while (cin >> n && n)
17     {
18         stack<ll> s;
19         ll MaxArea = 0;
20         for (int i = 0; i < n; i++)
21             cin >> h[i];
22         h[n] = -1;
23         int index = 0;
24         while (index <= n)
25         {
26             if (s.empty() || h[s.top()] < h[index])
27                 s.push(index++);
28             else
29             {
30                 ll t = s.top();
31                 s.pop();
32                 MaxArea=max(MaxArea,h[t]*(s.empty()?index:index-s.top()-1));
33             }
34         }
35         cout << MaxArea << endl;
36     }
37     return 0;
38 }

单调栈

原文：https://www.cnblogs.com/graytido/p/10745017.html