
1 #include <iostream> 2 #include <vector> 3 #include <queue> 4 #include <cstring> 5 using namespace std; 6 const int maxn = 1e5 + 10; 7 int T, n, m, u, v, num; 8 int InDeg[maxn];//入度 9 vector<int> vec[maxn];//邻接表 10 //判断是否有环 11 queue<int> q; 12 //复杂度0(v + e) 13 /* 14 2 15 2 2 16 1 2 17 2 1 18 3 2 19 1 2 20 1 3 21 输出 Wrong 22 Correct 23 */ 24 bool topsort(){ 25 while(!q.empty()){//清空队列 26 q.pop(); 27 } 28 int num=0;//记录被删去的节点数 29 for(int i = 1; i <= n; i++){ 30 if(!InDeg[i]){//将入度为0的顶点入队 31 q.push(i); 32 } 33 } 34 while(!q.empty()){ 35 int now = q.front(); 36 q.pop(); 37 num++; 38 //遍历当前元素下一个元素的所有元素 39 for(int i= 0;i < vec[now].size();i++){ 40 //与当前点连的,入度为1的入队(且减为0)度数大于1的度数减1但不入队,小于1的不影响 41 if(--InDeg[vec[now][i]] == 0){ 42 q.push(vec[now][i]); 43 } 44 } 45 } 46 //若删去的点等于原来图中点的个数则该有向图无环 47 if(num == n) return true; 48 return false; 49 } 50 int main(){ 51 scanf("%d", &T); 52 while(T--){ 53 scanf("%d%d", &n, &m);//读入n个顶点m条边 54 for(int i = 1; i <= n; i++){//清空该顶点到其他顶点的边 55 vec[i].clear(); 56 } 57 memset(InDeg, 0, sizeof(InDeg)); //将记录入度的数组清空 58 while(m--){//读入m条边 59 scanf("%d%d", &u,&v); 60 vec[u].push_back(v);//从u到v建立连接(有向图) 61 InDeg[v]++;//将v的入度加1 62 } 63 if(topsort()){ 64 puts("Correct"); 65 }else{ 66 puts("Wrong"); 67 } 68 } 69 return 0; 70 }
拓扑排序二
小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论,当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中,小Hi和小Ho整理得到了以下的信息:
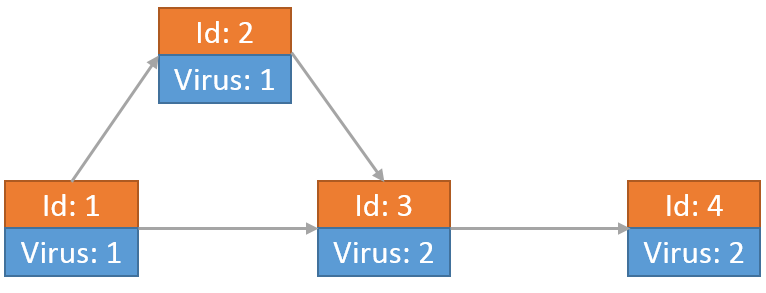
举个例子,假设切断部分网络连接后学校网络如下图所示,由4个节点和4条链接构成。最开始只有节点1上有病毒。
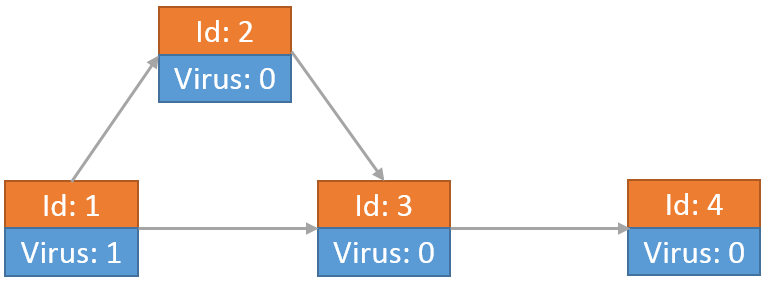
最开始节点1向节点2和节点3传送了病毒,自身留有1个病毒:
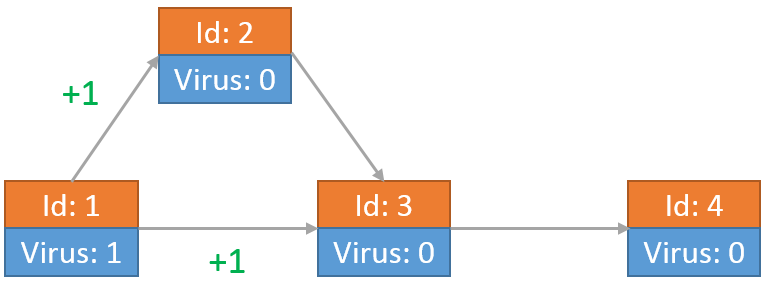
其中一个病毒到达节点2后,向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝:
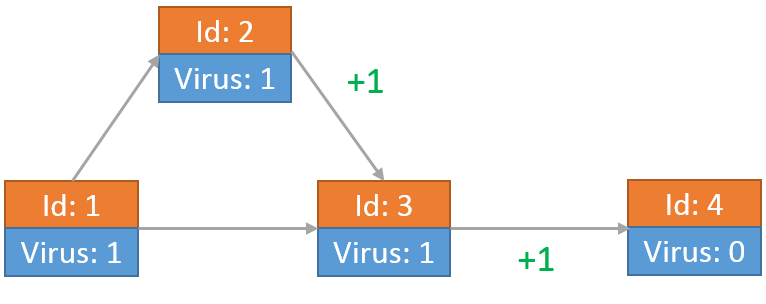
当从节点2传送到节点3的病毒到达之后,该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒:
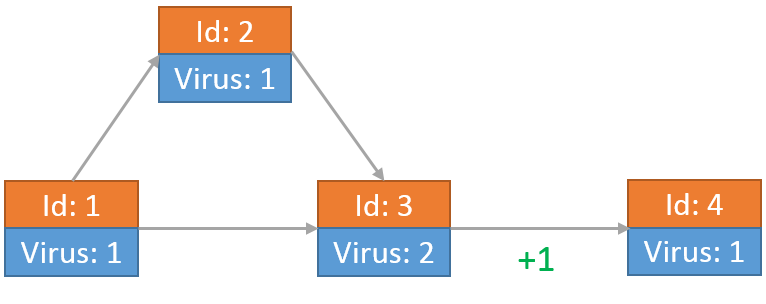
最后每个节点上的病毒为:
小Hi和小Ho根据目前的情况发现一段时间之后,所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说,最后会有多少个病毒呢?
第1行:3个整数N,M,K,1≤K≤N≤100,000,1≤M≤500,000
第2行:K个整数A[i],A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N
第3..M+2行:每行2个整数 u,v,表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N
第1行:1个整数,表示最后整个网络的病毒数量 MOD 142857
4 4 1 1 1 2 1 3 2 3 3 4
6
1 #include <iostream> 2 #include <vector> 3 #include <queue> 4 #include <cstring> 5 using namespace std; 6 const int maxn = 1e5 + 10; 7 const int mod = 142857; 8 int T, n, m, u, v; 9 int InDeg[maxn];//入度 10 int virus[maxn];//病毒的数量 11 vector<int> vec[maxn];//邻接表 12 queue<int> q; 13 //拓扑排序二 14 void topsort(){ 15 while(!q.empty()){//清空队列 16 q.pop(); 17 } 18 for(int i = 1; i <= n; i++){ 19 if(!InDeg[i]){//将入度为0的顶点入队 20 q.push(i); 21 } 22 } 23 while(!q.empty()){ 24 int now = q.front(); 25 q.pop(); 26 //遍历当前元素下一个元素的所有元素 27 for(int i= 0;i < vec[now].size();i++){ 28 //与当前点连的,入度为1的入队(且减为0)度数大于1的度数减1但不入队,小于1的不影响 29 if(--InDeg[vec[now][i]] == 0){ 30 q.push(vec[now][i]); 31 } 32 //与当前元素相连的元素的病毒数=(当前元素的病毒数+ 当前元素相连的元素的病毒数) % mod 33 virus[vec[now][i]] = (virus[vec[now][i]] + virus[now]) % mod; 34 } 35 } 36 37 } 38 int main(){ 39 int k, x; 40 while(~scanf("%d%d%d",&n,&m,&k)){ 41 for(int i = 1; i <= n; i++){//清空该顶点到其他顶点的边 42 vec[i].clear(); 43 } 44 memset(InDeg, 0, sizeof(InDeg)); //将记录入度的数组清空 45 memset(virus, 0, sizeof(virus)); 46 while(k--){ 47 scanf("%d",&x); 48 virus[x]++; 49 } 50 while(m--){//读入m条边 51 scanf("%d%d", &u,&v); 52 vec[u].push_back(v);//从u到v建立连接(有向图) 53 InDeg[v]++;//将v的入度加1 54 } 55 topsort(); 56 int ans = 0; 57 for(int i = 1; i <= n; i++){ 58 ans = (ans + virus[i]) % mod; 59 } 60 printf("%d\n",ans); 61 } 62 return 0; 63 }
In this winter holiday, Bob has a plan for skiing at the mountain resort.
This ski resort has MM different ski paths and NNdifferent flags situated at those turning points.
The ii-th path from the S_iSi?-th flag to the T_iTi?-th flag has length L_iLi?.
Each path must follow the principal of reduction of heights and the start point must be higher than the end point strictly.
An available ski trail would start from a flag, passing through several flags along the paths, and end at another flag.
Now, you should help Bob find the longest available ski trail in the ski resort.
The first line contains an integer TT, indicating that there are TT cases.
In each test case, the first line contains two integers NN and MM where 0 < N \leq 100000<N≤10000and 0 < M \leq 1000000<M≤100000 as described above.
Each of the following MM lines contains three integers S_iSi?, T_iTi?, and L_i~(0 < L_i < 1000)Li? (0<Li?<1000)describing a path in the ski resort.
For each test case, ouput one integer representing the length of the longest ski trail.
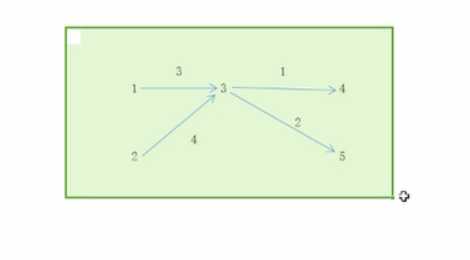
1 5 4 1 3 3 2 3 4 3 4 1 3 5 2
6
原文:https://www.cnblogs.com/AGoodDay/p/10745072.html