学习Machine Learning,阅读文献,看各种数学公式的推导,其实是一件很枯燥的事情。有的时候即使理解了数学推导过程,也仍然会一知半解,离自己写程序实现,似乎还有一道鸿沟。所幸的是,现在很多主流的Machine Learning方法,网上都有open source的实现,进一步的阅读这些源码,多做一些实验,有助于深入的理解方法。
Ranklib就是一套优秀的Learning to Rank领域的开源实现,其主页在:http://people.cs.umass.edu/~vdang/ranklib.html,从主页中可以看到实现了哪些方法。其中由微软发布的LambdaMART是IR业内常用的Learning to Rank模型,本文介绍RanklibV2.1(当前最新的时RanklibV2.3,应该大同小异)中的LambdaMART实现,用以帮助理解paper中阐述的方法。
LambdaMART.java中的LambdaMART.learn()是学习流程的管控函数,学习过程主要有下面四步构成:
1. 计算deltaNDCG以及lambda;
2. 以lambda作为label训练一棵regression tree;
3. 在tree的每个叶子节点通过预测的regression lambda值还原出gamma,即最终输出得分;
4. 用3的模型预测所有训练集合上的得分(+learningRate*gamma),然后用这个得分对每个query的结果排序,计算新的每个query的base ndcg,以此为基础回到第1步,组成森林。
重复这个步骤,直到满足下列两个收敛条件之一:
1. 树的个数达到训练参数设置;
2. Random Forest在validation集合上没有变好。
下面用一组实际的数据来说明整个计算过程,假设我们有10个query的训练数据,每个query下有10个doc,每个q-d对有10个feature,如下:
1 0 qid:1830 1:0.002736 2:0.000000 3:0.000000 4:0.000000 5:0.002736 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 2 0 qid:1830 1:0.025992 2:0.125000 3:0.000000 4:0.000000 5:0.027360 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 3 0 qid:1830 1:0.001368 2:0.000000 3:0.000000 4:0.000000 5:0.001368 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 4 1 qid:1830 1:0.188782 2:0.375000 3:0.333333 4:1.000000 5:0.195622 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 5 1 qid:1830 1:0.077975 2:0.500000 3:0.666667 4:0.000000 5:0.086183 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 6 0 qid:1830 1:0.075239 2:0.125000 3:0.333333 4:0.000000 5:0.077975 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 7 1 qid:1830 1:0.079343 2:0.250000 3:0.666667 4:0.000000 5:0.084815 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 8 1 qid:1830 1:0.147743 2:0.000000 3:0.000000 4:0.000000 5:0.147743 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 9 0 qid:1830 1:0.058824 2:0.000000 3:0.000000 4:0.000000 5:0.058824 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 10 0 qid:1830 1:0.071135 2:0.125000 3:0.333333 4:0.000000 5:0.073871 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 11 0 qid:1837 1:0.004065 2:0.000000 3:0.500000 4:0.000000 5:0.000000 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 12 0 qid:1837 1:0.459350 2:0.000000 3:0.000000 4:1.000000 5:0.455285 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 13 0 qid:1837 1:0.060976 2:0.333333 3:0.500000 4:0.000000 5:0.065041 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 14 0 qid:1837 1:0.093496 2:0.000000 3:0.000000 4:0.000000 5:0.085366 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 15 0 qid:1837 1:0.195122 2:0.000000 3:0.000000 4:0.000000 5:0.186992 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 16 0 qid:1837 1:0.036585 2:0.333333 3:0.500000 4:0.000000 5:0.040650 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 17 0 qid:1837 1:0.032520 2:0.000000 3:0.000000 4:0.000000 5:0.024390 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 18 0 qid:1837 1:0.073171 2:0.000000 3:0.000000 4:0.000000 5:0.065041 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 19 0 qid:1837 1:0.024390 2:1.000000 3:0.500000 4:1.000000 5:0.048780 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 20 0 qid:1837 1:0.024390 2:0.333333 3:0.500000 4:1.000000 5:0.032520 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 21 0 qid:1840 1:0.000000 2:0.000000 3:0.000000 4:0.000000 5:0.000000 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 22 1 qid:1840 1:0.007364 2:0.200000 3:1.000000 4:0.500000 5:0.013158 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 23 1 qid:1840 1:0.097202 2:0.000000 3:0.000000 4:0.000000 5:0.096491 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 24 2 qid:1840 1:0.169367 2:0.000000 3:0.500000 4:0.000000 5:0.169591 6:0.000000 7:0.000000 8:0.000000 9:0.000000 10:0.000000 25 ......
为了简便,省略了余下的数据。上面的数据格式是按照Ranklib readme中要求的格式组织(类似于svmlight),除了行号之外,第一列是q-d对的实际label(人标注数据),第二列是qid,后面10列都是feature。
这份数据每组qid中的doc初始顺序可以是随机的,也可以是从实际的系统中获得的当前顺序。总之这个是计算ndcg的初始状态。对于qid=1830,它的10个doc的初始顺序的label序列是:0, 0, 0, 1, 1, 0, 1, 1, 0, 0(虽然这份序列中只有label值为0和1的,实际中也会有2,3等,由自己的标注标准决定)。我们知道dcg的计算公式是:
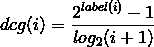
i表示当前doc在这个qid下的位置(从1开始,避免分母为0),label(i)是doc(i)的标注值。而一个query的dcg则是其下所有doc的加和:
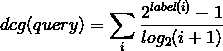
根据上式可以计算初始状态下每个qid的dcg:
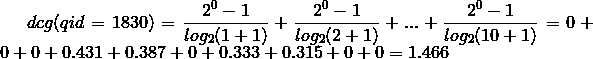
要计算ndcg,还需要计算理想集的dcg,将初始状态按照label排序,qid=1830得到的序列是1,1,1,1,0,0,0,0,0,0,计算dcg:
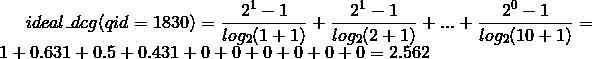
两者相除得到初始状态下qid=1830的ndcg:
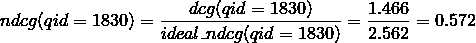
下面要计算每一个doc的deltaNDCG,公式如下:
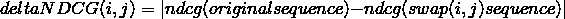
deltaNDCG(i,j)是将位置i和位置j的位置互换后产生的ndcg变化(其他位置均不变),显然有相同label的deltaNDCG(i,j)=0。
在qid=1830的初始序列0, 0, 0, 1, 1, 0, 1, 1, 0, 0,由于前3的label都一样,所以deltaNDCG(1,2)=deltaNDCG(1,3)=0,不为0的是deltaNDCG(1,4), deltaNDCG(1,5), deltaNDCG(1,7), deltaNDCG(1,8)。
将1,4位置互换,序列变为1, 0, 0, 0, 1, 0, 1, 1, 0, 0,计算得到dcg=2.036,整个deltaNDCG(1,4)的计算过程如下:
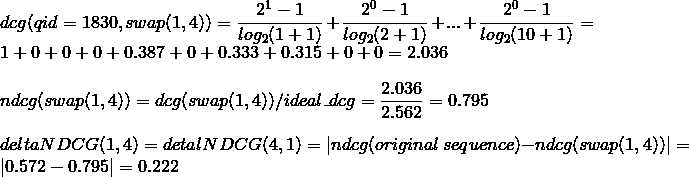
同样过程可以计算出deltaNDCG(1,5)=0.239, deltaNDCG(1,7)=0.260, deltaNDCG(1,8)=0.267等。
进一步,要计算lambda(i),根据paper,还需要ρ值,ρ可以理解为doci比docj差的概率,其计算公式为:
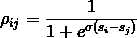
Ranklib中直接取σ=1(σ的值决定rho的S曲线陡峭程度),如下图,蓝,红,绿三种颜色分别对应σ=1,2,4时ρ函数的曲线情形(横坐标是si-sj):

初始时,模型为空,所有模型预测得分都是0,所以si=sj=0,ρij≡1/2,lambda(i,j)的计算公式为:
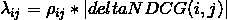
上式为Ranklib中实际使用的公式,而在paper中,还需要再乘以-σ,在σ=1时,就是符号正好相反,这两种方式应该是等价的,符号并不影响模型训练结果。而:
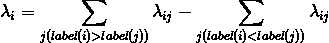
计算lambda(1),由于label(1)=0,qid=1830中的其他doc的label都大于或者等于0,所以lamda(1)的计算中所有的lambda(1,j)都为负项。将之前计算的各deltaNDCG(1,j)代入,且初始状态下ρij≡1/2,所以:
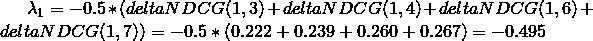
可以计算出初始状态下qid=1830各个doc的lambda值,如下:
1 qId=1830 0.000 0.000 0.000 -0.111 -0.120 0.000 -0.130 -0.134 0.000 0.000 lambda(1): -0.495 2 qId=1830 0.000 0.000 0.000 -0.039 -0.048 0.000 -0.058 -0.062 0.000 0.000 lambda(2): -0.206 3 qId=1830 0.000 0.000 0.000 -0.014 -0.022 0.000 -0.033 -0.036 0.000 0.000 lambda(3): -0.104 4 qId=1830 0.111 0.039 0.014 0.000 0.000 0.015 0.000 0.000 0.025 0.028 lambda(4): 0.231 5 qId=1830 0.120 0.048 0.022 0.000 0.000 0.006 0.000 0.000 0.017 0.019 lambda(5): 0.231 6 qId=1830 0.000 0.000 0.000 -0.015 -0.006 0.000 -0.004 -0.008 0.000 0.000 lambda(6): -0.033 7 qId=1830 0.130 0.058 0.033 0.000 0.000 0.004 0.000 0.000 0.006 0.009 lambda(7): 0.240 8 qId=1830 0.134 0.062 0.036 0.000 0.000 0.008 0.000 0.000 0.003 0.005 lambda(8): 0.247 9 qId=1830 0.000 0.000 0.000 -0.025 -0.017 0.000 -0.006 -0.003 0.000 0.000 lambda(9): -0.051 10 qId=1830 0.000 0.000 0.000 -0.028 -0.019 0.000 -0.009 -0.005 0.000 0.000 lambda(10): -0.061
上表中每一列都是考虑了符号的lamda(i,j),即如果label(i)<label(j),则为负值,反之为正值,每行结尾的lamda(i)是前面的加和,即为最终的lambda(i)。
可以看到,lambda(i)在系统中表达了doc(i)上升或者下降的强度,label越高,位置越后,lambda(i)为正值,越大,表示趋向上升的方向,力度也越大;label越小,位置越靠前,lambda(i)为负值,越小,表示趋向下降的方向,力度也大(lambda(i)的绝对值表达了力度。)
然后Regression Tree开始以每个doc的lamda值为目标,训练模型。
LambdaMART简介——基于Ranklib源码(一 lambda计算),布布扣,bubuko.com
LambdaMART简介——基于Ranklib源码(一 lambda计算)
原文:http://www.cnblogs.com/wowarsenal/p/3900359.html