他的孩子二叉树1. 为是优先队列?
普通的队列是一种先进先出的数据结构,元素在队列尾追加,而从队列头删除。在优先队列中,元素被赋予优先级。当访问元素时,具有最高优先级的元素最先删除。优先队列具有最高级先出 (first in, largest out)的行为特征。通常采用堆数据结构来实现。
2. 为什么使用优先队列?
在1000000000个元素选出前100名?
对于总共N个请求,使用普通数组或顺序数组,最差情况:O(n^2)。使用堆:O(nlogn)
3. 优先队列的实现?
可以看到利用堆这种数据结构可以很好平衡入队和出队的时间复杂度。

4. 二叉堆的实现(Binary heap)
满足的性质:二叉树的任何一个节点都不大于其父节点;是一颗完全二叉树:除了最后一层,每层的结点数都必须是最大值。
满足这种条件的二叉堆也叫最大堆。
使用数组就可以存储一个二叉堆,这是因为二叉堆是一颗完全二叉树。
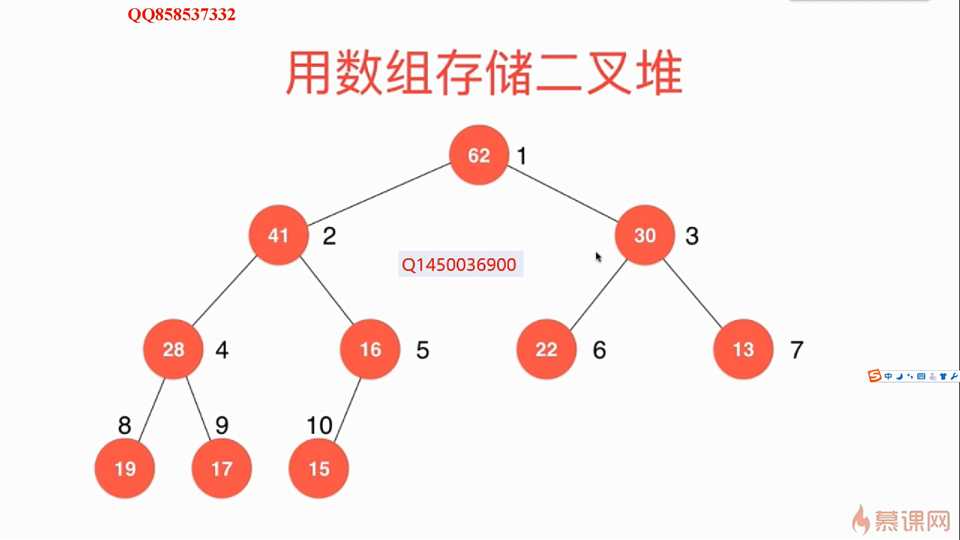
注意根节点的索引是1。那么根据父节点与子节点的关系,就可以将元素存放到如下:
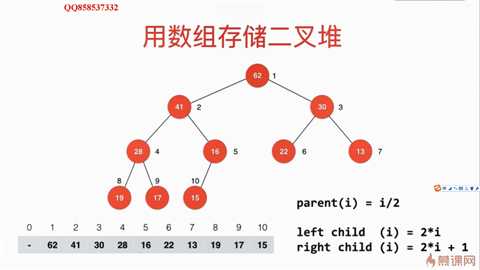
那么如何向一个最大堆插入元素呢?
下面展示了利用Shift Up的算法来插入元素并维护一个最大堆的过程:先插入一个元素52,此时不满足最大堆的性质,因为52的父亲16比他小。
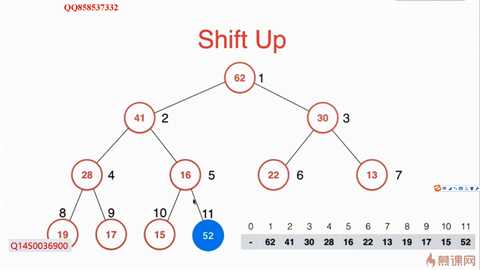
所以需要将52连续和其父结点交换顺序,直到满足父节点比子节点都大的性质:
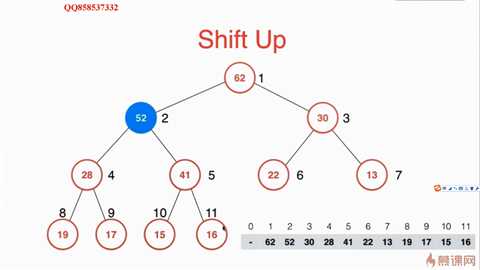
那么如何从最大堆删除一个元素呢?
下面展示了利用Shift down的算法来删除元素并维护一个最大堆的过程:依照性质,删除的元素是堆中第一个位置的元素,也即最大的元素。那删除下图中62之后,怎么填补空位?应该将最后一个元素填补到第一个位置来维护这个完全二叉树。
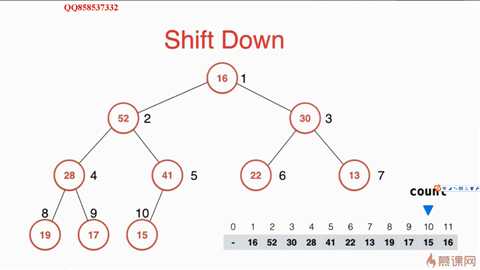
此时这个完全二叉树不满足父节点都比子节点大的性质。所以16需要和他的孩子进行交换,但是和左孩子还是有孩子呢?应该比较一下,谁大和谁交换!只有这样才使得父节点最大!
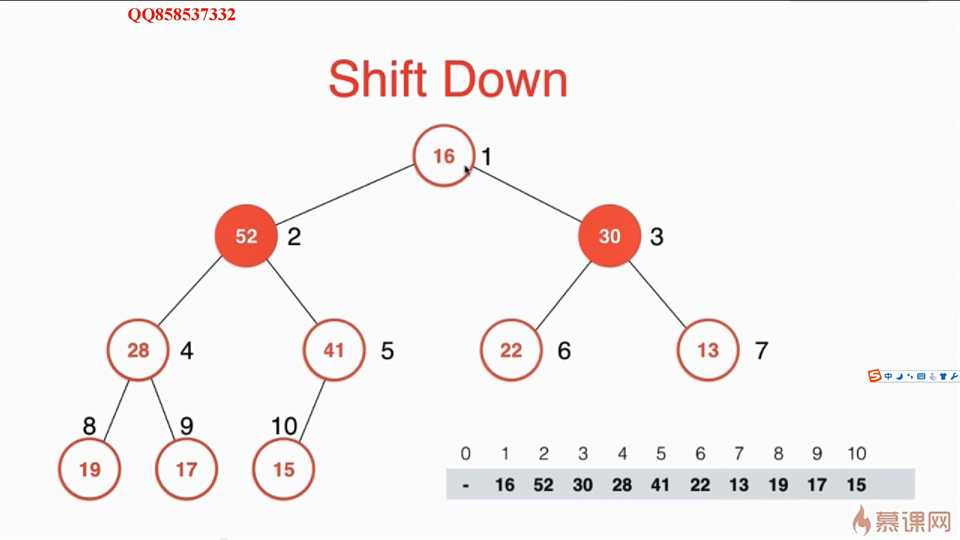
最后维护后的最大堆为:
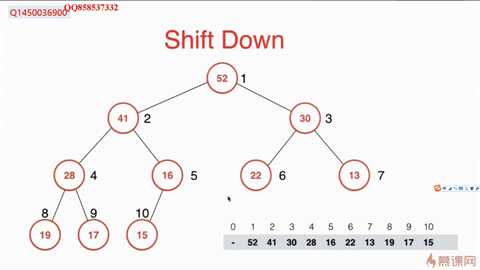
注:所有插图均来自慕课网。
原文:https://www.cnblogs.com/king-lps/p/10778324.html