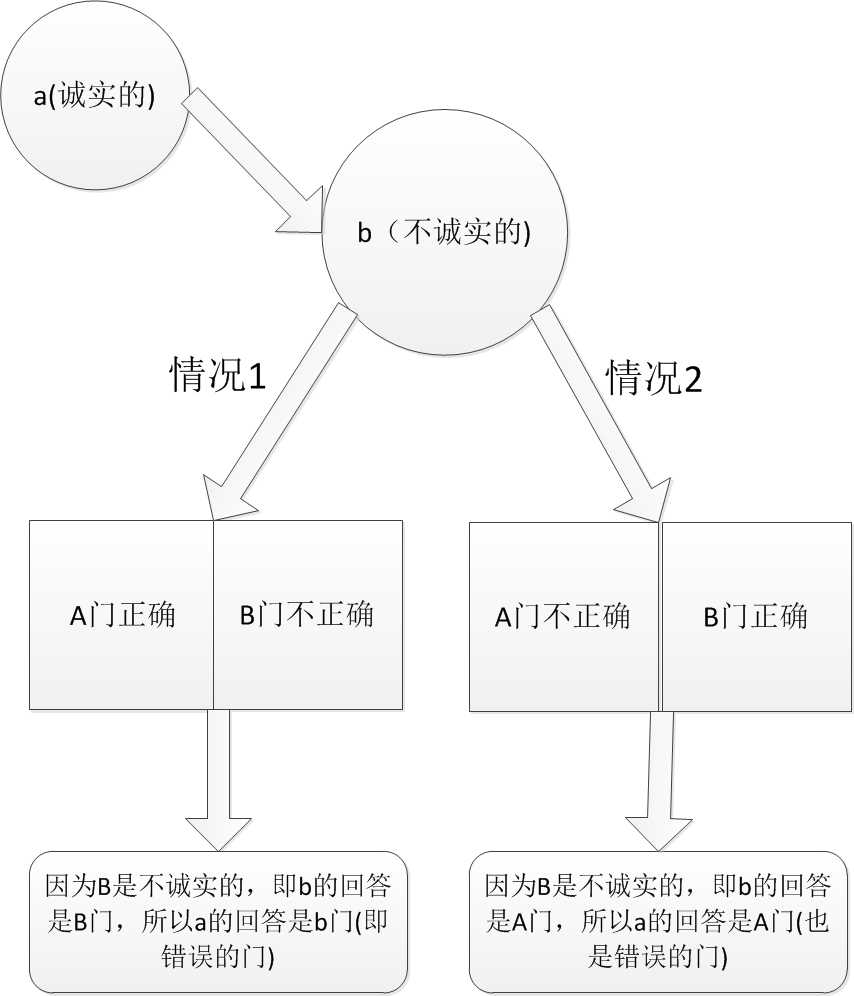
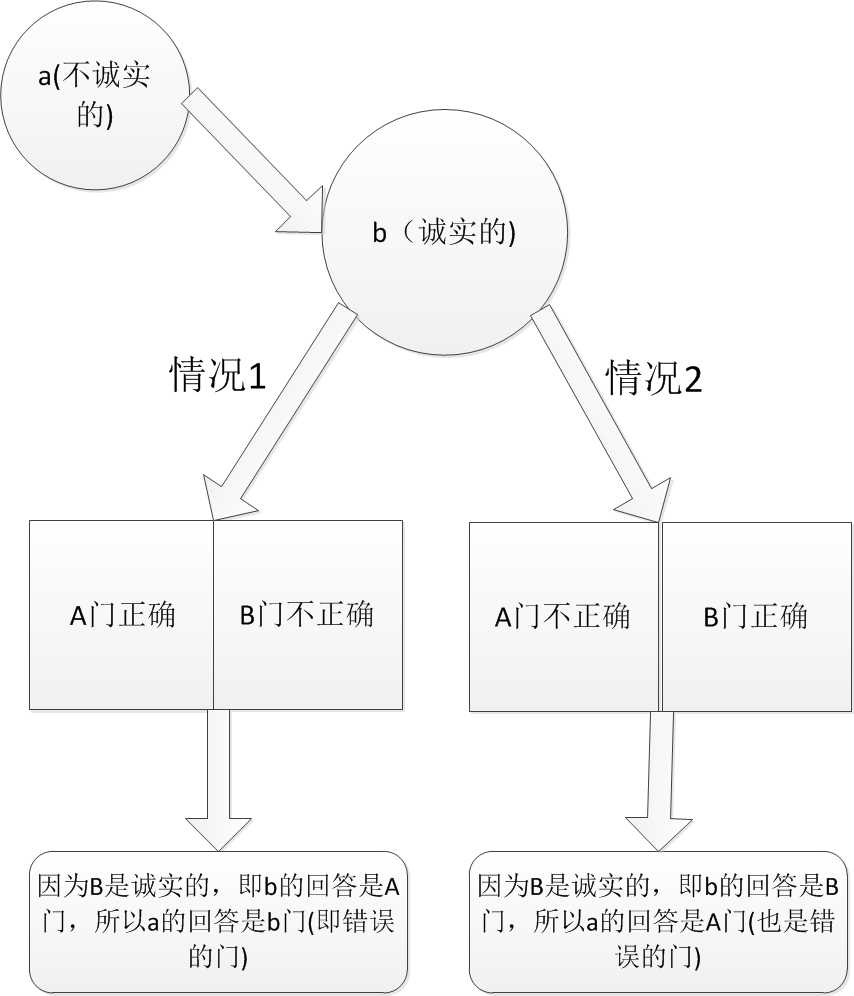
所以无论第一个问的人是诚实的还会说谎的,得到的答案都是错误的那个门,所以正确的门马上就能知道了
这题是比较有意思的,当初的我天真的以为5人平均分,1人20就共同生存,皆大欢喜了。知道答案后才知道自己太天真了.....首先这个问题不能从A开始开始,而是应该从后往前考虑,即逆向推导,并且还要注意的一个原则,生命诚可贵,即前提一定是自己要活下来。在前面的人一定是最惨的,因为稍有分配不慎,就会被集体投票处决,相反,第5个人一定是最安全的,因为如果前面4个人都被投票处死,那么E就可以独吞了。如果ABC都死了,那么E一定会把D处死,因为只有两个人,无法出现超过半数票同意决策的情况,所以D一定不会让C死掉,所以3号的决策一定是让自己获得最大利益->如果AB都死的话,C的决策一定是(100,0,0).但是B如果不死呢,就不会轮到C决策了,所以B的决策一定会为自己拉到赞成票,即D和E的票,给他们一人1个,相比C的决策一个都拿不到,得到一个也是很不错的了,所以B的分配会是(98,0,1,1),这样无论C同不同意,都会执行决策。好,最后到到A,A一定知道BCD他们的如意算盘,所以,A会保住自己的性命,并且拿到最多的的金币。所以A只要让另外两个人支持自己可以了,同时A要获得最大利益,所以A会这样分配(1号方案(97,0,1,2,0)或 2 号方案(97,0,1,0,2))。1、2号方案都是自己拿97,这是最大利益了,为什么呢??1号方案给了C 1个,D 2个,这样D一定会支持他,因为如果A死了,B的决策只会让D自己拿到1个,肯定拿2个利益大啊。同理,B的决策不会给C金币,A这里给了1个,当然最好不过了。E不给也行,不影响最终决策通过。2号方案,(97,0,1,0,2)C的票是肯定赞成的,E这里拿了两个,也会赞成,B不用给,D不用给,也不影响决策通过。这里给E一个可以吗??答案是不行的,因为A和B的方案都是给E一个,所以D可以赞成A和B的任何一个,A为了保险,会多给一个。当然,不管哪个方案,自己都会拿97个走。
第一个问题:你是诚实的吗??
第二个问题:根据上一个问题的回答可分为:谁是诚实的?、谁不是诚实的?
为什么这么问呢?第一个问题,因为5个人都不确定,所以问谁都一样,但是,我们可以根据第一个问题的回答推测出他下一个问题回答正确型来针对性的提出第二个问题.
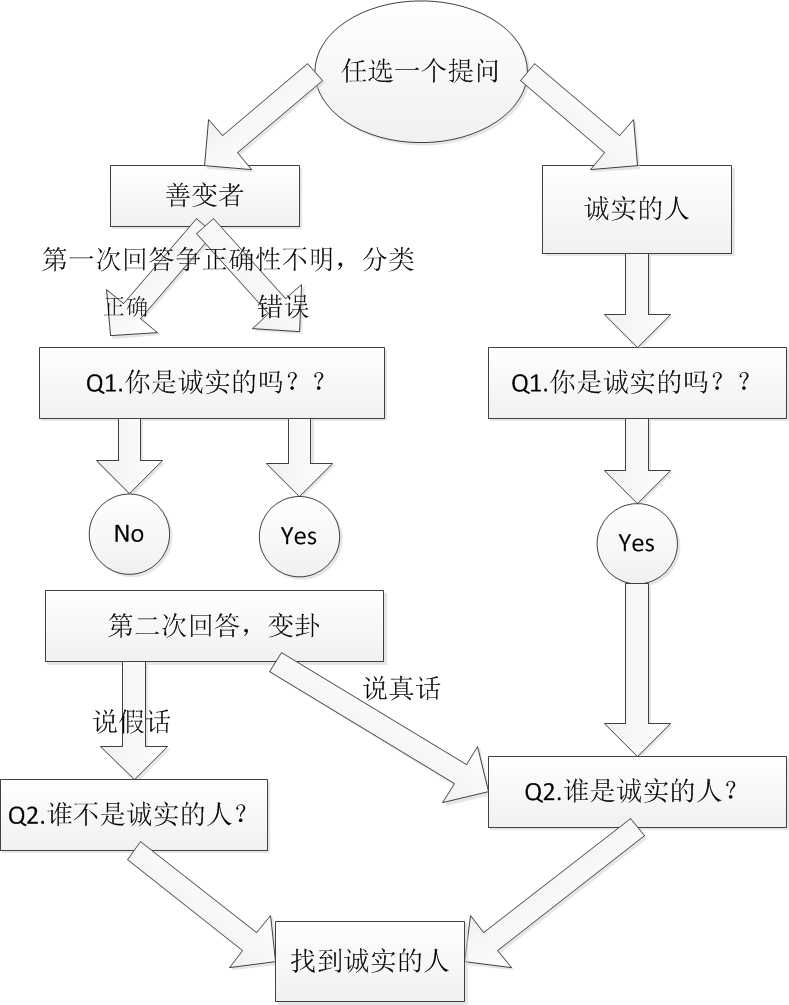
由于第一次提问身份不明,所以只能根据对一个问题的回答得出下一次回答的正确性,第一次回答Yes后,只能是诚实的人的回答或是善变者的第一次欺骗,那么无论接下来继续问什么问题,都会得到正确答案,所以第二个问题直接问是谁就好了。如果第一个问题回答是No,只能是善变者的的第一次正确回答,那么下一次回答一定是错误的,为了将错就错,问他谁不是诚实的人,他一定会说出诚实的人,因为要欺骗啊,所以最终都得出诚实的人。
为什么.5呢?因为最后一个人只能看运气。因为排队顺序不确定。所以大家定这样一个规则,最后一个人根据前面一种帽子的数量做决策,如果黑色帽子数为奇数,则回答黑色,如果为偶数,则回答白色。当然,这个壮举保证了前面9个人活了下来,自己只能看运气了。如果最后一个回答是黑色,即前9个人中有奇数个带黑色帽子的,这下第9个人数一下前8个人的黑色帽子数,如果是奇数,那么自己的帽子一定是白色,回答白色就行,如果黑色帽子数为偶数,那么自己一定是黑色帽子,回答黑色就行。这时,到8号回答,他会根据第10个人的回答判断黑色帽子的数量,在根据第9个的回答判断黑色帽子的数量.....一直到1号

原文:https://www.cnblogs.com/ygsworld/p/10796443.html