poj 1179 Polygon (区间dp)

时间：2019-05-01 19:38:40 阅读：141 评论：0 收藏：0 [点我收藏+]

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.
技术分享图片

On the first move, one of the edges is removed. Subsequent moves involve the following steps:
?pick an edge E and the two vertices V1 and V2 that are linked by E; and
?replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.
技术分享图片

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices‘ labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

t -7 t 4 x 2 x 5

Sample Output

1 2

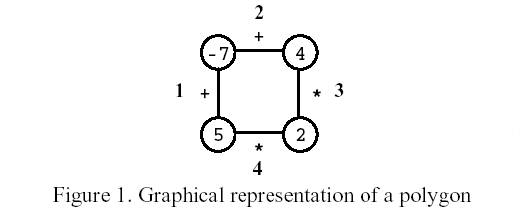
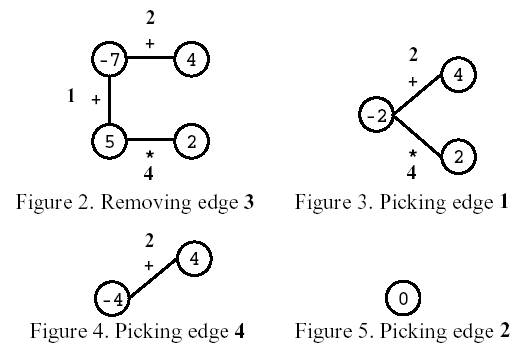
题意:已知一个环形的圆有n个点和n条边现在让你任意去掉一条边然后每次根据边的符号合并两个点要求合并成1个点的最大值

思路:和石子合并很像我们只需要把链扩大为原来的两倍在这个长度上dp就行了值得注意的是最大值可能由两个最小值相乘得到所以我们既要维护最大值同时也要记录最小值

在这个思路上区间dp即可

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<map>
#include<queue>
#define ll long long int
using namespace std;
inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
int moth[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int dir[4][2]={1,0 ,0,1 ,-1,0 ,0,-1};
int dirs[8][2]={1,0 ,0,1 ,-1,0 ,0,-1, -1,-1 ,-1,1 ,1,-1 ,1,1};
const int inf=0x3f3f3f3f;
const ll mod=1e9+7;
int dp[107][107][2];
char op[107];
int a[107];
int arry[107];
int main(){
    ios::sync_with_stdio(false);
    int n;
    while(cin>>n){
        for(int i=1;i<=n;i++){
            cin>>op[i]>>a[i];
            a[i+n]=a[i];
            op[i+n]=op[i];  //两倍长链 
        }
        for(int i=1;i<=2*n;i++) //初始化边界 
            for(int j=1;j<=2*n;j++)
                dp[i][j][1]=inf,dp[i][j][0]=-inf;
        for(int i=1;i<=2*n;i++){
            dp[i][i][0]=dp[i][i][1]=a[i]; //处理边界 
        }
        for(int len=2;len<=n;len++) //长度 
            for(int i=1;i+len<=2*n;i++){ //起点 
                int j=i+len-1;
                for(int k=i;k<j;k++){ //分割点 
                    if(op[k+1]==‘t‘){
                        dp[i][j][0]=max(dp[i][j][0],dp[i][k][0]+dp[k+1][j][0]);
                        dp[i][j][1]=min(dp[i][j][1],dp[i][k][1]+dp[k+1][j][1]);
                    }else{
                        dp[i][j][0]=max(dp[i][j][0],
                        max(dp[i][k][1]*dp[k+1][j][1],dp[i][k][0]*dp[k+1][j][0]));
                        
                        dp[i][j][1]=min(dp[i][j][1],
                        min(dp[i][k][1]*dp[k+1][j][0],
                        min(dp[i][k][1]*dp[k+1][j][1],dp[i][k][0]*dp[k+1][j][1])));
                    }    
                }
            }
        int ans=-inf;
        int sz=0;
        for(int i=1;i<=n;i++){
            if(ans<dp[i][i+n-1][0]){
                ans=dp[i][i+n-1][0];
                sz=1;
                arry[sz]=i;
            }else if(ans==dp[i][i+n-1][0]){
                arry[++sz]=i;
            }
        }
        cout<<ans<<endl;
        for(int i=1;i<=sz;i++){
            if(i==1)
            cout<<arry[i];
            else cout<<" "<<arry[i];
        }
        cout<<endl;
    } 
    return 0;
}

poj 1179 Polygon (区间dp)

原文：https://www.cnblogs.com/wmj6/p/10800468.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)