from: https://blog.csdn.net/yangang908/article/details/62215209
and : https://my.oschina.net/xiaoluobutou/blog/688245
先验概率:
事件发生前的预判概率。可以是基于历史数据的统计,可以由背景常识得出,也可以是人的主观观点给出。一般都是单独事件概率,如P(x),P(y)。
后验概率:
事件发生后求的反向条件概率;或者说,基于先验概率求得的反向条件概率。概率形式与条件概率相同。
条件概率:
一个事件发生后另一个事件发生的概率。一般的形式为P(x|y)表示y发生的条件下x发生的概率。
贝叶斯公式:
P(y|x) = ( P(x|y) * P(y) ) / P(x)
这里:
P(y|x) 是后验概率,一般是我们求解的目标。
P(x|y) 是条件概率,又叫似然概率,一般是通过历史数据统计得到。一般不把它叫做先验概率,但从定义上也符合先验定义。
P(y) 是先验概率,一般都是人主观给出的。贝叶斯中的先验概率一般特指它。
P(x) 其实也是先验概率,只是在贝叶斯的很多应用中不重要(因为只要最大后验不求绝对值),需要时往往用全概率公式计算得到。
实例:假设y是文章种类,是一个枚举值;x是向量,表示文章中各个单词的出现次数。
在拥有训练集的情况下,显然除了后验概率P(y|x)中的x来自一篇新文章无法得到,p(x),p(y),p(x|y)都是可以在抽样集合上统计出的。
最大似然理论:
认为P(x|y)最大的类别y,就是当前文档所属类别。即Max P(x|y) = Max p(x1|y)*p(x2|y)*...p(xn|y), for all y
贝叶斯理论:
认为需要增加先验概率p(y),因为有可能某个y是很稀有的类别几千年才看见一次,即使P(x|y)很高,也很可能不是它。
所以y = Max P(x|y) * P(y), 其中p(y)一般是数据集里统计出来的。
从上例来讲,贝叶斯理论显然更合理一些;但实际中很多先验概率是拍脑袋得出的(不准),有些甚至是为了方便求解方便生造出来的(硬凑),那有先验又有什么好处呢?一般攻击贝叶斯都在于这一点。
条件概率公式:
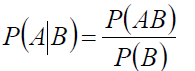
全概率公式:
![]()
贝叶斯公式:
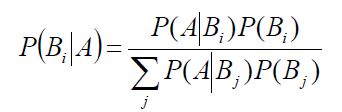
给定某系统的若干样本X,计算该系统的参数,即
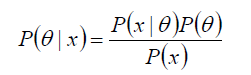
P(θ) 没有数据支持下,θ发生的概率:先验概率
P(θ|x) 在数据X的支持下,θ发生的概率:后验概率,贝叶斯公式也称为后验公式
p(x|θ) 给定某参数θ的概率分布:似然函数
理解:
1) 教科书上的解释总是太绕了,有一个很好例子:在没有给任何信息的前提下,让猜某人的姓氏。为了猜对概率大一些,你可能会先百度一下中国人口的姓氏排名,发现李姓是中国第一大姓,约占全国汉族人口的7.94%,所以你可能会猜李。也就是李姓出现在的概率最大。
此时李姓的概率即为 先验概率
2) 接着有人给提供了一些跟这个人相关信息,比如:知道他是来自”赵家村“,那这个时候你就知道,他姓赵的概率比较大,就会猜姓赵。
此时P(姓赵|赵家村)这个条件概率,即为 后验概率
3) 似然函数:
由贝叶斯公式带来的思考:
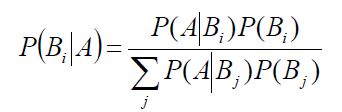
给定某些样本A,在这些样本中计算结论B1,B2....Bi出现的概率,即P(Bi|A),拿概率最大的那个结论B做为样本A最终的结论,也就是说我要求max P(Bi|A),由贝叶斯公式:
max P(Bi|A) = max P(A|Bi)P(Bi)/P(A)
其中 P(A) 即 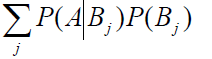
又因为样本A给定,对于B1,B2....Bi来说P(A)是相同的,可以把分母去掉:
max P(Bi|A) => max P(A|Bi)P(Bi)
若这些结论B1,B2....Bi的先验概率相等(或者近似),则可以得到:
max P(Bi|A) => max P(A|Bi)P(Bi)=> max P(A|Bi)
最后得到结论,我们求maxP(Bi|A),实际跟求max P(A|Bi)是等价的 而P(A|Bi)就是似然函数
原文:https://www.cnblogs.com/Arborday/p/10801675.html