今天主讲图论。
前言:图的定义:图G是一个有序二元组(V,E),其中V称为顶集(Vertices Set),E称为边集(Edges set),E与V不相交。它们亦可写成V(G)和E(G)。
一、图的存储:
1、邻接矩阵:

2、邻接表:
数组模拟链表实现:记录每条边的终点、边权(如果有的话)、同一起点的上一条边的编号,并记录以每个点为起点的最后一条边的编号。
STL中的vector:记录以每个点为起点的边。
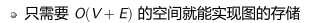
一些vector的细节:
vector 本质就是 c++ 模板库帮我们实现好的可以变长的数组
向一个数组(vector型) a 的末尾加入一个元素 x a.push_back(x)
询问 a 的长度 a.size(),询问a的真实长度a.capacity()
注意:vector 中元素下标从 0 开始,当需要变长时,变长一倍,因此需要额外的内存空间。
深入学习:https://www.cnblogs.com/zhonghuasong/p/5975979.html
代码:
邻接表:
const int N = 5005;//最多N个点/边 struct edge { int u, v, w, next;//起点,终点,边权,同起点的上一条边的编号 }edg[N]; int head[N]; //以每个点为起点的最后一条边的编号 int n, m, cnt; //cnt: 边的总数 void add(int u, int v, int w) { int e = ++cnt; edg[e] = (edge){u, v, w, head[u]}; head[u] = e; } int main() { cin >> n >> m; cnt = 0; for (int u, v, w, i = 1; i <= m; i++) cin >> u >> v >> w, add(u, v, w), odeg[u]++, ideg[v]++; return 0; }
vector:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const int N = 5005; 6 7 struct edge { 8 int u, v, w; 9 }; 10 vector<edge> edg[N]; 11 int n, m, cnt; //cnt: numbers of edges 12 bool visited[N]; 13 14 void add(int u, int v, int w) 15 { 16 edg[u].push_back((edge){u, v, w}); 17 } 18 void travel(int u, int distance)//遍历 19 { 20 cout << u << " " << distance << endl; visited[u] = true; 21 for (int e = 0; e < edg[u].size(); e++) 22 if (!visited[edg[u][e].v]) 23 travel(edg[u][e].v, distance + edg[u][e].w); 24 } 25 int main() 26 { 27 cin >> n >> m; cnt = 0; 28 for (int u, v, w, i = 1; i <= m; i++) 29 cin >> u >> v >> w, add(u, v, w); 30 return 0; 31 } 32
二、生成树

最小生成树:给定一个 n 个点 m 条边的带权无向图,求一个生成树,使得生成
树中边权和的最小。
例题引入:

扩展(引用百度百科):
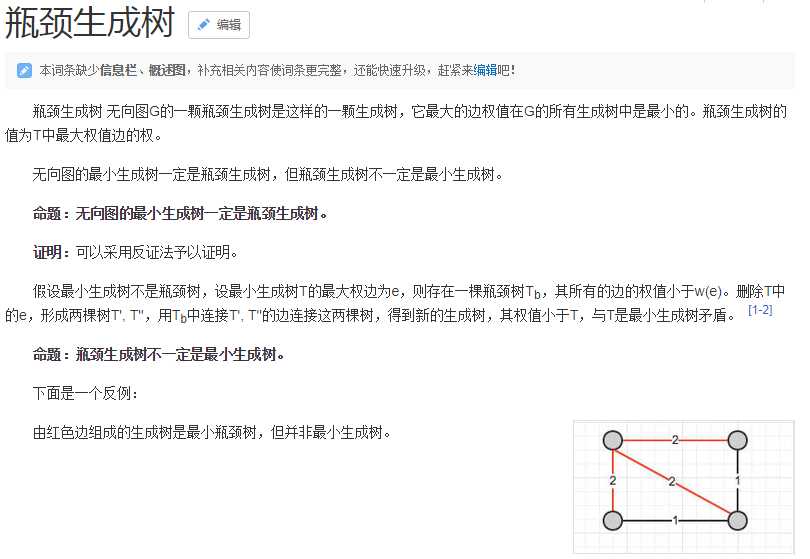
只要求出最小生成树就好了。
求解最小生成树:
生成树的本质:选取若干条边使得任意两点连通。
各种求解算法的本质:贪心
1、Kruskal算法(克鲁斯卡尔算法):
将所有边按边权排好序,从最小的开始枚举:若加入该边后,会形成环(即边的端点已经连通),就忽略掉它,看下一条;否则加入该边,直至得到最小生成树(能得到的话)。查询两点连通情况:并查集。
时间复杂度:O(E log E)
代码:
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 const int maxn = 1000005; 6 struct edge { 7 int u, v, w; 8 }edg[maxn]; 9 int n, m, p[maxn], ans = 0; 10 11 bool cmp(edge a, edge b) 12 {return a.w < b.w;} 13 int findp(int t) 14 {return p[t] ? p[t] = findp(p[t]) : t;} 15 bool merge(int u, int v) 16 { 17 u = findp(u); v = findp(v); 18 if (u == v) return false; 19 p[u] = v; return true; 20 } 21 int main() 22 { 23 cin >> n >> m; 24 for (int i = 1, u, v, w; i <= m; i++) 25 cin >> u >> v >> w, edg[i] = (edge){u, v, w}; 26 sort(edg + 1, edg + m + 1, cmp); 27 28 for (int i = 1; i <= m; i++) 29 if (merge(edg[i].u, edg[i].v)) 30 ans = max(ans, edg[i]. w); 31 cout << ans << endl; 32 }
2、Prim算法(普里姆算法):
以一点为最小生成树的根,找到一个到该最小连通块边权最小、不在该连通块里的点,并加入到该连通块,直到组成最小生成树。
时间复杂度:O(n2)
代码:
#include<iostream> #include<cstdio> #include<cstring> #define forup(i,n) for(int i=1;i<=n;i++)//偷懒 using namespace std; int n,m; int ma[5001][5001],bianli=1,d[5001]; bool vis[5001]; int main() { int x,y,z,tot=0; cin>>n>>m; memset(ma,0x3f,sizeof(ma));//求最短性图论问题一般初始化为一个很大的数 forup(i,m) { scanf("%d%d%d",&x,&y,&z);//去重边 if(z<ma[x][y]) ma[x][y]=ma[y][x]=z; } vis[1]=1; memset(d,0x3f,sizeof(d)); d[1]=0; memset(vis,0,sizeof(vis));//0蓝1白 int stt_node,stt_dis; forup(i,n) { stt_dis=0x3f3f3f3f,stt_node=0; for(int j=1;j<=n;j++) if(!vis[j]&&d[j]<stt_dis) { stt_node=j; stt_dis=d[j]; } vis[stt_node]=1; tot+=stt_dis; for(int j=1;j<=n;j++) if(!vis[j]&&d[j]>ma[j][stt_node]) { d[j]=ma[j][stt_node]; } } cout<<tot; return 0; }
三、路径
最短路径问题:
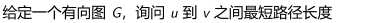

最短路径算法本质思想:不断进行松弛操作(更新最短路操作)
1、Floyd算法(弗洛伊德算法):

正确性:
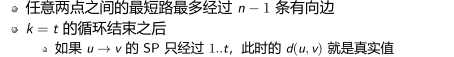
可求任意两点之间的最短路(多源最短路),时间复杂度O(n);
负权环:

2、Bellman-Ford算法(贝尔曼-福特算法)
单源最短路算法,设源点为S
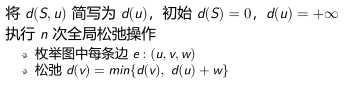
正确性:
d[u]至少经过1条边,经过几条边,用几条边松弛后就能得到真实值。任意最短路经过不超过 n − 1 条边,n 次松弛足矣。
 因此不适用于有负权环的情况。(n为点数,m为边数)
因此不适用于有负权环的情况。(n为点数,m为边数)
易知Bellman-Ford 算法中,如果 d(u) 在上一次全局更新中没有被更新,那么这一次全局更新中不必松弛 u 的出边(若能更新,上一次就不会不更新)。
3.SPFA算法(Shortest Path Faster Algorithm 翻译:最短路径快速算法(在一般情况下的确挺快的,只要不被针对))
贝尔曼-福特算法的队列优化形式,通过队列减少了很多冗余的计算,时间复杂度O(kE)(k是小常数,平均值为2)最糟糕的时间复杂度O(VE)(被针对的恐惧)
原文:https://www.cnblogs.com/InductiveSorting-QYF/p/10803250.html