目录
(略)
int32_t和int64_t类型,指明数据的长度
//按照字节打印数据中的内容
#include<bits/stdc++.h>
using namespace std;
typedef unsigned char *byte_pointer;
void show_bytes(byte_pointer start, int len){
int i;
for(i = 0; i < len; ++i){
printf(" %.2x", start[i]);
}
printf("\n");
}
void show_int(int x){
show_bytes((byte_pointer)&x, sizeof(int));
}
int main(){
int num;
cin >> num;
show_int(num);
return 0;
}\([x_{\omega - 1}, x_{\omega - 2}, ..., x_0]\)
假设整型数据类型有\(\omega\)位,将其表示记作位向量\(\vec x = [x_{\omega - 1}, x_{\omega - 2}, \cdots, x_0]\)
\[ B2U_{\omega}(\vec x)=\sum_{i=0}^{\omega - 1} x_i 2 ^ i \]
范围:\(Umax = \sum\limits_{i = 0}^{\omega - 1} 2 ^ i = 2 ^\omega -1\)
示例:
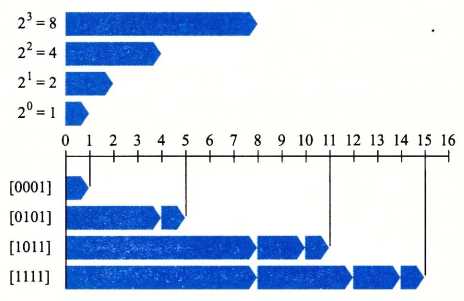
定义:
\[
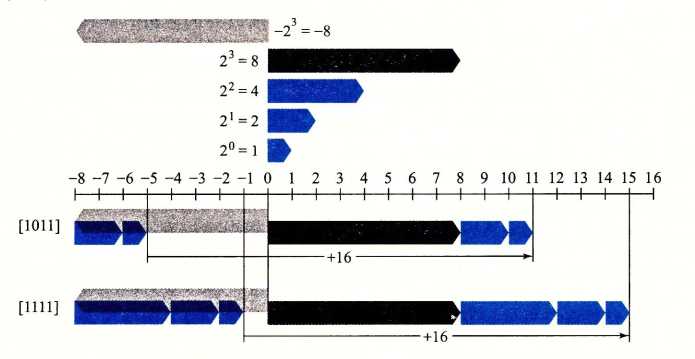
B2T_{\omega}(\vec x) = -x_{\omega - 1}2^{\omega - 1} + \sum_{i = 0}^{\omega - 2}x_i 2 ^i【注】补码表示中,最高位被理解为负权
\]
【注】补码表示中,最高位被理解为负权
范围:\(Tmin = -2^{\omega - 1}, Tmax = \sum\limits_{i = 0} ^ {\omega - 2}2 ^ i = 2 ^{\omega - 1} - 1\)
示例:
定理:\(B2T_\omega(\vec x)\)是一个双射
【注】
补码和无符号数:\(Umax = 2Tmax + 1\)
所有机器都将有符号数表示为补码,尽管C语言标准没有明确规定
\[ B2S_\omega(\vec x) = (-1)^{x_{\omega - 1}}\times \sum_{i = 0}^{\omega - 2}x_i2^i \]
补码转为无符号数:
\[
T2U_\omega(x) = \begin{cases}
x + 2 ^\omega & x < 0,\x & x \geq 0
\end{cases}
\]
推导:
\[ \begin{align} B2U_\omega (\vec x) - B2T_\omega(\vec x) &= x_{\omega - 1}2^\omega \Longrightarrow B2U_\omega(\vec x) = x_{\omega - 1}2^\omega + B2T_\omega(\vec x)\T2U_\omega(x) &= B2U_\omega(T2B_\omega(x)) \&= x_{\omega -1}2^\omega + B2T_{\omega}(T2B_\omega)(x)\&= x_{\omega- 1}2^\omega + x \end{align} \]
\[ U2T_{\omega}(x) = \begin{cases} u & u \leq Tmax_\omega \u - 2 ^ \omega & u > Tmax_\omega \end{cases} \]

\[ x_\omega = [x_{\omega - 1}, \cdots, x_0]\longrightarrow x'_{\omega + k} = [\underbrace{x_{\omega-1}, \cdots, x_{\omega - 1}}_{k个}, x_{\omega - 1}, \cdots, x_0] \]
\[ \vec x = [x_{\omega -1 }, \cdots, x_0], \vec x' = [x_{k-1}, \cdots, x_0]\x' = x \mod 2^k \]
\[ \vec x = [x_{\omega -1 }, \cdots, x_0], \vec x' = [x_{k-1}, \cdots, x_0]\x' = U2T_k(x\mod 2^k) \]
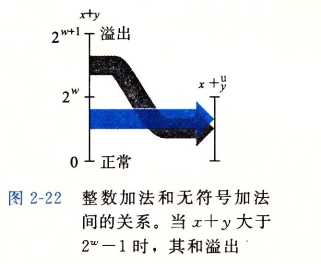
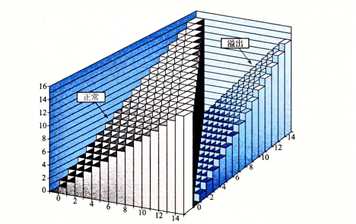
对于满足\(0\leq x, y < 2^\omega\),有:
\[
x+_\omega^u y = \begin{cases}
x + y & x + y < 2 ^ \omega \x + y - 2 ^ \omega & x + y \geq 2 ^\omega
\end{cases}
\]
\[ -_\omega^u x = \begin{cases} x & x = 0\2^\omega - x & x > 0 \end{cases} \]
\[ x+_\omega^t y=\begin{cases} x+y-2^\omega & 2 ^{\omega - 1} \leq x + y\x+y & -2^{\omega -1 } \leq x + y < 2 ^{\omega -1}\x+y+2^\omega &x + y < -2^{\omega -1} \end{cases} \]
【注】还是来源于截断,当没有溢出时,不发生截断;溢出的情况只会是“正+正”或者“负+负”;“正+正”溢出时,符号位为0,数字部分的最高位变为1(进位导致增加的数字),截断后原有的符号位会被丢弃,符号位变为1,真实的值为\(x+y=2^{\omega -1} + \sum\limits_{i=0}^{\omega -2}x_i2^i\),截断后的值为\(x+_\omega^t y- = 2^{\omega -1} + \sum\limits_{i=0}^{\omega -2}x_i2^i\),因此\(x+_\omega^t y = x + y - 2^\omega\);负溢出解释相似。
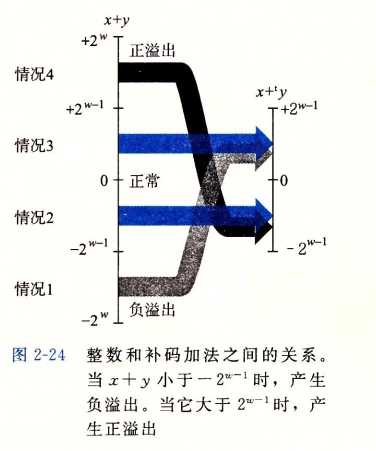
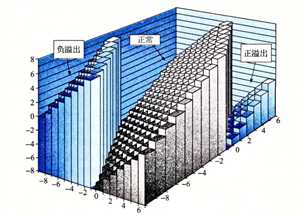
有符号和无符号具有相同的位级表示,因此先将参数转换为无符号数,然后按照无符号数运算,最后将结果转换为补码
\[
\begin{align}
x+_\omega^u y &= U2T_\omega(T2U_\omega(x) + T2U_\omega(y))\&= U2T_\omega((x_{\omega-1}2^\omega + y_{\omega - 1}2^\omega+x+y)\mod 2^\omega)\&= U2T_\omega((x+y)\mod 2^\omega)
\end{align}
\]
记\(z=x+y, z' = z\mod 2^\omega, z'' = U2T_\omega(z')\)
若\(-2^{\omega}\leq z < -2^{\omega-1}\),则\(z'=z+2^\omega\),因此\(0\leq z' < 2^{\omega -1}\),故\(z''=z'\)
其余三种情况以此类推
\[ -_\omega^tx=\begin{cases} Tmin &x = Tmin\-x & x>Tmin \end{cases} \]
给定长度为\(\omega\)的位向量\(\vec x, \vec y\),用补码形式定义的整数为\(x, y\),用无符号定义的整数为\(x', y'\),则:
\[
T2B_\omega(x*_\omega^t y) = U2B_\omega(x'*_\omega^u y')
\]
证明
\[
\begin{align}
(x'*y')\mod 2^\omega &= ((x_{\omega -1}2^\omega+x) \cdot (y_{\omega -1}2^\omega + y))\mod 2^\omega\&= (xy)\mod 2^\omega\T2U_\omega(x*_\omega^t y)&=T2U_\omega(U2T_\omega((x\cdot y)\mod 2^\omega))\&= x\cdot y \mod 2^\omega\T2B_\omega(x*_\omega^t y)&=U2B_\omega(T2U_\omega(x*_\omega^t y))\&=U2B_\omega((x\cdot y)\mod 2^\omega)
\end{align}
\]
对于无符号数,\(x>>k\)产生数值\(\lfloor x/2^k\rfloor\)
对于有符号数
\(x>0\)时同无符号数
\(x<0\)时,\(x>>k\)产生数值\(\lfloor x/2^k\rfloor\),\((x+(1<<k) - 1)>>k\)产生数值\(\lceil x/2^k\rceil\)
偏置的设计:
注意到$\lceil x/y\rceil = \lfloor (x+y-1)/y\rfloor \(,设\)x = qy+r\(,因此\)\lfloor (x+y-1)/y\rfloor=q+\lfloor(r+y-1)/y\rfloor\(,当\)r\(为0时,后面一项为0,当\)r>0\(时后面为1。取\)y=2^k$,即可得到带偏置的除法公式
原文:https://www.cnblogs.com/vinnson/p/10807107.html