本章学习的内容是树和二叉树,在利用数组进行存储的顺序二叉树或者利用链表进行存储的链式二叉树的基础上展开了二叉树的遍历。
遍历又分为前序、中序和后序遍历,根据节点的顺序来命名。
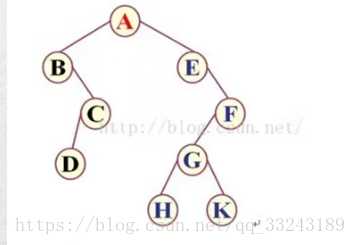
二叉树遍历结果会因为遍历使用的方式不同而不同,比如上图二叉树遍历结果
前序遍历:ABCDEFGHK
中序遍历:BDCAEHGKF
后序遍历:DCBHKGFEA
先序遍历
void PreOrderTraversal(BinTree BT)
{
if( BT )
{
printf(“%d\n”, BT->Data); //对节点做些访问比如打印
PreOrderTraversal(BT->Left); //访问左儿子
PreOrderTraversal(BT->Right); //访问右儿子
}
}
中序遍历算法
void InOrderTraversal(BinTree BT)
{
if(BT)
{
InOrderTraversal(BT->Left);
printf("%d\n", BT->Data);
InOrderTraversal(BT->Right);
}
}
后序遍历算法
void PostOrderTraversal(BinTree BT)
{
if (BT)
{
PostOrderTraversal(BT->Left);
PostOrderTraversal(BT->Right);
printf("%d\n", BT->Data);
}
}
对于pta上面的实践1再解决过程中也遇到了一些问题,比如两棵树怎么对各个节点的值进行比较,如果两棵树不同位置的数据一样那么要用怎么样的方式来进行比较并且说明。最终在室友的提醒下,让我知道只需要对,某一节点的值进行比较然后一次比较它的双亲的数据值,就可以实现对整棵树的数据比较。
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
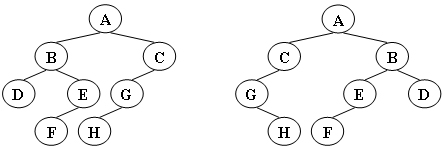
图1
图2
输入给出2棵二叉树树的信息。对于每棵树,首先在一行中给出一个非负整数N (≤10),即该树的结点数(此时假设结点从0到N−1编号);随后N行,第i行对应编号第i个结点,给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空,则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意:题目保证每个结点中存储的字母是不同的。
如果两棵树是同构的,输出“Yes”,否则输出“No”。
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -
Yes
8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4
No
代码
#include <iostream>
using namespace std;
typedef struct TreeNode //定义一个树的结构
{
char data; //结点的数据
char parent; //结点的双亲
}TreeNode;
bool input_output() //boll类型函数判断二叉树是否同构
{
int i,j; //定义参数
TreeNode tree1[10],tree2[10]; //定义两个数的结构
char ltree,rtree; //定义两个字符参数
int n; //定义结点数参数
cin>>n; //输入第一棵树的结点数
for(i=0;i<n;i++)
{
tree1[i].parent=‘0‘; //将第一棵树的所有结点的parent赋值为‘0‘
}
for(i=0;i<n;i++)
{
cin>>tree1[i].data; //输入结点数据
cin>>ltree>>rtree; //输入结点对应的左右子结点
if(ltree!=‘-‘) //若子结点不为空
{
j=ltree-48; //字符类型转换为int型,得到结点对应下标
tree1[j].parent = tree1[i].data ; //将结点的data值赋给子结点的parent
}
if(rtree!=‘-‘) //若子结点不为空
{
j=rtree-48; //字符类型转换为int型,得到结点对应下标
tree1[j].parent = tree1[i].data; //将结点的data值赋给子结点的parent
}
}
int m; //定义结点数参数
cin>>m; //输入第二棵树的结点数
for(i=0;i<m;i++)
{
tree2[i].parent=‘0‘; //将第二棵树的所有结点的parent赋值为‘0‘
}
for(i=0;i<m;i++)
{
cin>>tree2[i].data; //输入结点数据
cin>>ltree>>rtree; //输入结点对应的左右子结点
if(ltree!=‘-‘) //若子结点不为空
{
j=ltree-48; //字符类型转换为int型,得到结点对应下标
tree2[j].parent = tree2[i].data; //将结点的data值赋给子结点的parent
}
if(rtree!=‘-‘) //若子结点不为空
{
j=rtree-48; //字符类型转换为int型,得到结点对应下标
tree2[j].parent = tree2[i].data; //将结点的data值赋给子结点的parent
}
}
if(m!=n)return false; //若结点数不同,返回flase
if(m==1&&n==1&&tree1[0].data==tree2[0].data)return true; //结点数都为1,直接比较数据值,若为真则返回true
else if(m==1&&n==1&&tree1[0].data!=tree2[0].data)return false; //若为假则返回false
for(i=0;i<n;i++)
{
for(j=0;j<m;j++)
{
if(tree1[i].data==tree2[j].data) //若两棵树的某一结点数据值相同,则比较其双亲
{
if(tree1[i].parent!=tree2[j].parent) //若双亲不同,则返回false
{
return false;
}
}
}
}
return true; //双亲相同,返回true
}
int main()
{
bool a = input_output(); //定义bool型参数
if(a)cout<<"Yes"; //两棵树同构,输出“Yes”
else cout<<"No"; //两棵树不同构,输出“No”
return 0;
}
原文:https://www.cnblogs.com/xhongk/p/10816757.html