【机器学习】聚类分析的模型评估

　　一、聚类算法中的距离

　　1. 单个样本之间的距离

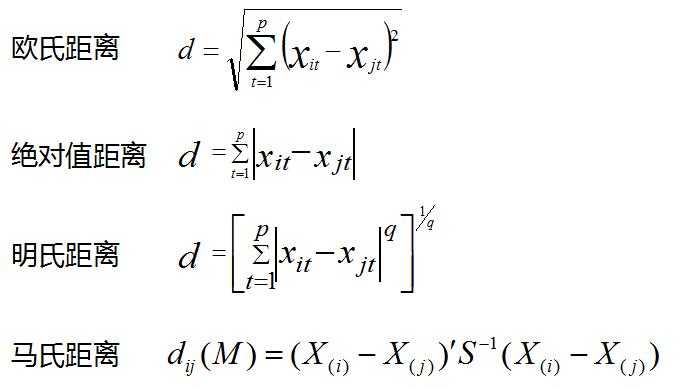
　　余弦距离     

　　在聚类分析中，一般需要对数据进行标准化，因为聚类数据会受数据量纲的影响。

　　在sklearn库中，可调用如下方法进行标准化：

1 from sklearn.preprocessing import StandardScaler
2 data = StandardScaler().fit_transform(data)

　　这种方法将data的均值和方差保存下来，并使用它们对数据进行归一化，这样，有新的数据输入时，仍可以沿用data的均值和方差来做归一化。

　　【联】facenet中是采用的L2归一化，这和每个向量自身相关，而不是和整体数据相关。

　　在上述距离中，受量纲影响较大的是明氏距离和欧氏距离（明氏距离的特例），马氏距离和余弦距离则受量纲影响较小。

　　其中，余弦距离越大（趋近于1），代表两个向量的方向越接近，相似度越高。

　　2. 两个聚类簇之间的距离

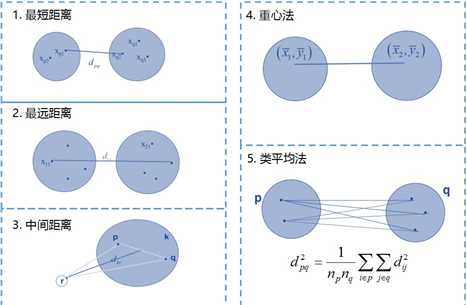
　　二、聚类算法的评价

　　评价聚类分群的最佳数量与分群效果。

　　1. 轮廓系数（silhouette coefficient）

　　轮廓系数这一指标无需知道数据集的真实标签。

　　取值范围[-1, 1]，值越大，聚类效果越好。旨在将某个对象与自己的簇的相似程度和与其他簇的相似程度作比较。轮廓系数最高的簇的数量表示簇的数量的最佳选择。

　　轮廓系数综合考虑了内聚度和分离度两种因素。

　　簇内不相似度a_i：计算样本i到所属簇内其他样本的平均距离a_i，将a_i定义为样本i的簇内不相似度，簇C中所有样本的a_i的均值为簇C的簇不相似度。

　　簇间不相似度b_i：计算样本i到其他某簇C_j的所有样本的平均距离b_ij，称为样本i与簇C_j的不相似度，将b_i=min{b_i1, b_i2, ... b_ik}定义为样本i的簇间不相似度。

　　样本i的轮廓系数：

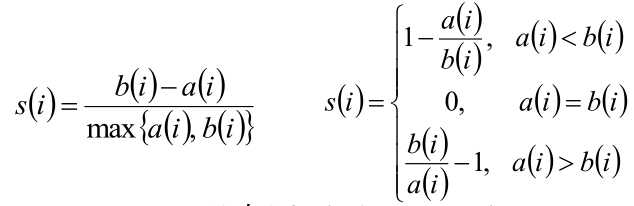
　　Si越接近1，则说明样本i的聚类合理；Si越接近-1，则说明样本越应该被分到其他簇内；S_i近似为0，则说明样本i近似在两个簇的边界上。

　　聚类结果的轮廓系数：所有样本的S_i的均值。该系数越大，聚类效果越好。

1 from sklearn import metrics
2 metrics.silhouette_score(data, labels)

　　2. 调整兰德指数（adjusted rand index）

　　兰德指数需要知道实际的类别信息C，设K为聚类结果。用a表示在C、K中都是同一类别的元素的对数，用b表示在C、K中都是不同类别的元素的对数，则兰德指数为

　　其中表示数据集中可以组成的总的元素对数。RI的取值范围为[0, 1]，值越大，意味着聚类结果与真实情况越吻合。

　　对于随机姐u共，RI并不能保证分数接近0。为了实现“在聚类结果随机产生的情况下，指标应该接近0”，提出了调整兰德指数，它具有更高的区分度：

　　ARI的取值范围为[-1, 1]，值越大意味着聚类结果与真实情况越吻合。从广义角度来讲，ARI衡量的是两个数据分布的吻合程度。

1 metrics.adjusted_rand_score(labels_true, labels_pred)

　　3. 互信息（mutual information）

　　MI也用来衡量两个数据分布的吻合程度。

　　假设U与V是对N个样本的分配情况，则两种分布的熵分别为

　　其中

　　则U与V之间的互信息MI定义为

　　其中

　　标准化后的互信息NMI为

　　与ARI类似，调整互信息（adjusted mutual information)为

　　MI与NMI的取值范围为[0, 1]，AMI的取值范围为[-1,1]，它们都是值越大意味着聚类结果与真实情况越吻合。

1 metrics.adjusted_mutual_info_score(labels_true, labels_pred)

 　　4. 同质性（homogeneity），完整性（completeness）和二者的调和平均（v-measure）

　　同质性：每个簇只包含单个类的成员

　　完整性：给定类的所有成员都分配给同一个簇

1 metrics.homogeneity_score(labels_true, labels_pred)
2 metrics.completeness_score(labels_true, labels_pred)
3 metrics.v_measure_score(labels_true, labels_pred)

　　5. Calinski-Harabaz index

　　数据类内协方差越小越好，类间协方差越大越好，calinski harabaz指数越高。

　　它和轮廓系数一样，可以在数据真实标签不知道的情况下，对聚类效果进行评估。似乎比轮廓系数的计算更快。

1 metrics.calinski_harabaz_score(data, labels)

 更多参考：

sklearn中的模型评估-构建评估函数

sklearn-clustering官方文档 

（2.3.9 clustering performance evaluation，注意advantages&drawbacks）

【机器学习】聚类分析的模型评估

原文：https://www.cnblogs.com/cry-star/p/10815553.html