




1 #include <iostream> 2 #include <string> 3 #include <iomanip> 4 using namespace std; 5 6 void dijsktra(int n, int **arc); 7 8 int main(){ 9 int n;//节点数 10 int m;//边数 11 int a, b, c; 12 int **arc;//邻接矩阵 13 cout << "输入图的节点个数和边的条数:" << endl; 14 cin >> n >> m; 15 //初始化邻接矩阵 16 arc = new int*[n]; 17 for (int i = 0; i < n; i++){ 18 arc[i] = new int[n]; 19 for (int j = 0; j < n; j++){ 20 if (i == j) arc[i][j] = 0; 21 else arc[i][j] = INT_MAX; 22 } 23 } 24 //邻接矩阵赋值 25 cout << "请输入每条边的起点和终点(节点编号从1开始)以及其权重" << endl; 26 for (int i = 0; i < m; i++){ 27 cin >> a >> b >> c; 28 arc[a - 1][b - 1] = c; 29 } 30 dijsktra(n, arc); 31 //释放内存 32 for (int i = 0; i < n; i++) 33 { 34 delete[] arc[i]; 35 } 36 delete[] arc; 37 } 38 39 void dijsktra(int n, int **arc){ 40 bool *s = new bool[n]; 41 int *dis = new int[n]; 42 string *path = new string[n]; 43 //给定源点 44 string path_s = "n1"; 45 s[0] = true; 46 dis[0] = 0; 47 path[0] = path_s + "→n1"; 48 //初始化s、dis、path 49 for (int i = 1; i < n; i++) 50 { 51 s[i] = false; 52 dis[i] = arc[0][i]; 53 path[i] = path_s + "→n" + to_string(i+1); 54 } 55 56 //打印邻接矩阵 57 cout << "\n图的邻接矩阵初始化为:" << endl; 58 int count_row = 0; //打印行的标签 59 int count_col = 0; //打印列的标签 60 while (count_row != n) { 61 count_col = 0; 62 while (count_col != n) { 63 if (arc[count_row][count_col] == INT_MAX) 64 cout << "∞" << " ";//按住Alt键不放,依次按下小键盘中的“41438”,再放开Alt健,“∞”就显示在屏幕中了 65 else 66 cout << arc[count_row][count_col] << " "; 67 ++count_col; 68 } 69 cout << endl; 70 ++count_row; 71 } 72 73 //开始迭代 74 for (int i = 1; i < n; i++) 75 { 76 //搜索U中的dis最小值节点v_temp 77 int dis_min = INT_MAX;//记录U中dis最小值 78 int temp = 0;//记录dis最小节点下标 79 for (int j = 0; j < n; j++) 80 { 81 if (s[j] == false && dis[j] < dis_min) 82 { 83 temp = i; 84 dis_min = dis[j]; 85 } 86 } 87 s[temp] = true;//dis最小节点加入S 88 89 //搜索v_temp出S外的邻接点做松弛操作 90 for (int k = 1; k < n; k++) 91 { 92 if (s[k] == false && arc[temp][k] != INT_MAX) 93 {//搜寻到v_temp到v_k得路径 94 if (dis[k]>dis[temp] + arc[temp][k]) 95 { 96 dis[k] = dis[temp] + arc[temp][k]; 97 path[k] = path[temp] + "→n" + to_string(k + 1);//箭头搜狗输入法符号大全 98 } 99 } 100 } 101 } 102 103 //输出最短路径搜索结果 104 cout << "\n" << "以n1" << "为起点的图的最短路径为:" << endl; 105 cout.flags(ios::left); 106 cout << setw(8) << "起点 " << setw(8) << "终点 " << setw(10) << "最短路径" << setw(10) << "节点序列" << endl; 107 for (int i = 0; i < n; i++){ 108 //cout.flags(ios::left); 109 if (dis[i]!= INT_MAX) 110 cout << setw(8) << "n1" << "n" << setw(7) << (i + 1) << setw(10) << dis[i] << path[i] << endl; 111 else 112 cout << setw(8) << "n1" << "n" << setw(7) << (i + 1) << setw(10) << dis[i] << "无最短路径" << endl; 113 } 114 }
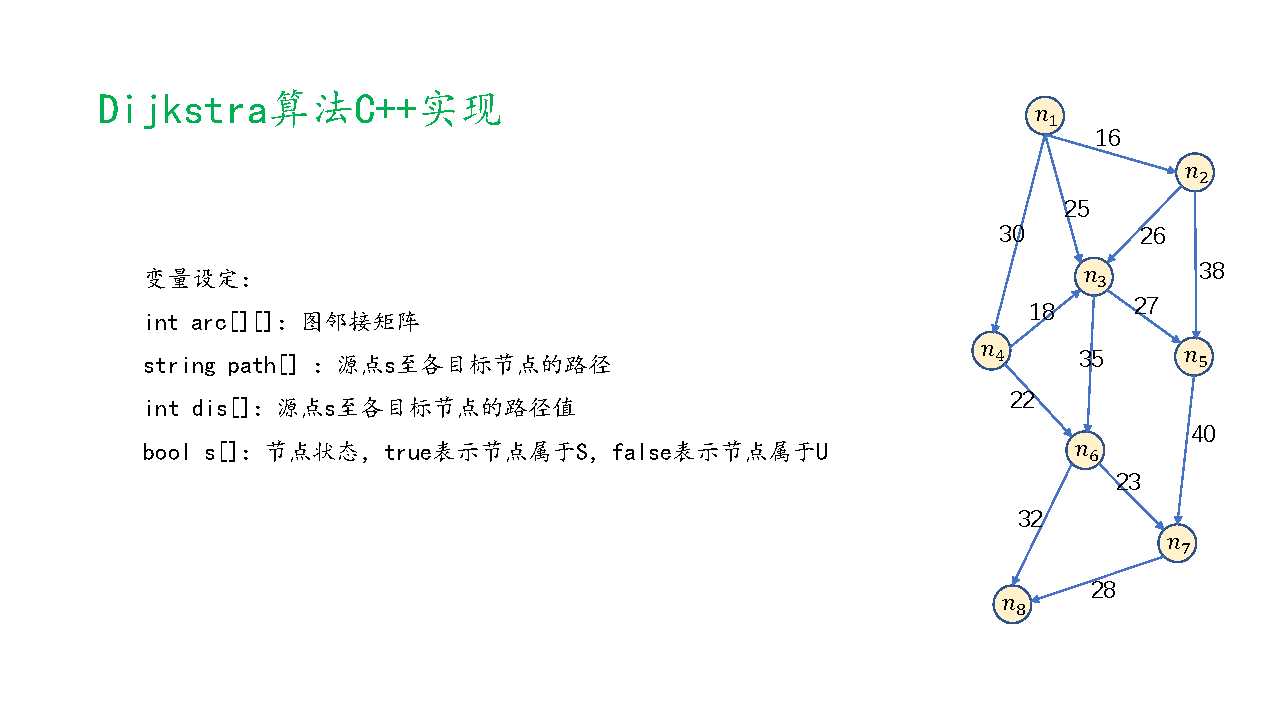
武汉地铁站点最短路径搜索的实现(一)——Dijkstra算法(coding)
原文:https://www.cnblogs.com/bkyjc/p/10822491.html