给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。

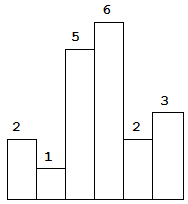
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3] 输出: 10
解答:本题可以用堆栈来进行处理。为了更好的处理数据,本题采用顺序递增栈来处理。为了能够处理最后一个高度,我们做了个小处理,首先给栈 s 压入值 0 。具体逻辑如下:
【1】如果直方图高度依次递增,那么就依次压入直方图的index;
【2】如果直方图不符合递增,那么开始处理数据:res = max(res , 最小高度 * 距离);
//84 int largestRectangleArea(vector<int> &height) { int res=0; stack<int> s; height.push_back(0);//in order to accumulate the last number: height[n] for(int i=0;i<(signed)height.size();i++) { if(s.empty() || height[i]>height[s.top()]) s.push(i); else { int curr = s.top(); s.pop(); res = max(res,height[curr]* (s.empty()? i:i-s.top()-1)); i--; } } return res; }//84
原文:https://www.cnblogs.com/2Bthebest1/p/10834525.html