机器学习建模介绍：
①分类②回归③聚类④时序分析（不常用）
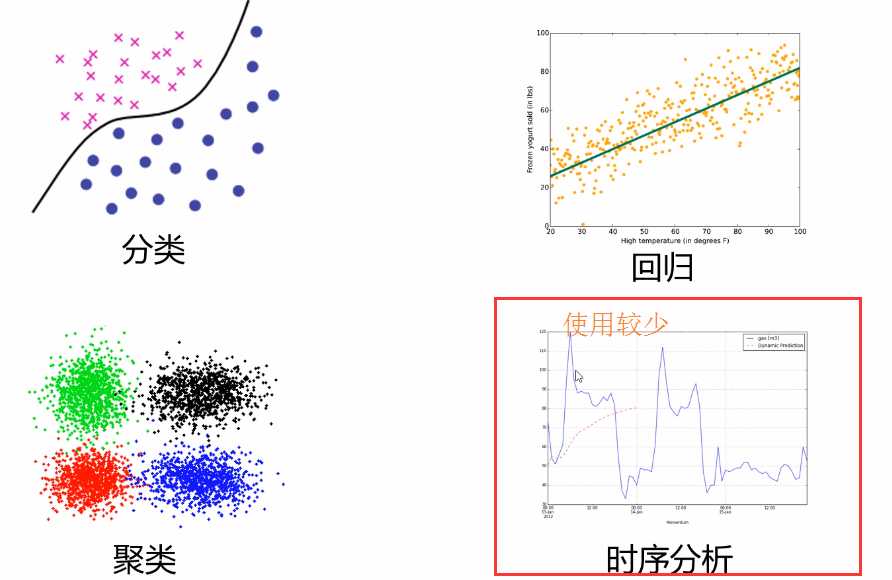
1，分类：
应用：人脸识别、垃圾邮件检测、信用卡申请人风险评估等
原理：
1）将数据映射到预先定义的类
2）把具有某些特征的数据项映射到给定的某个类别上
我们需要通过学习出分类的边界
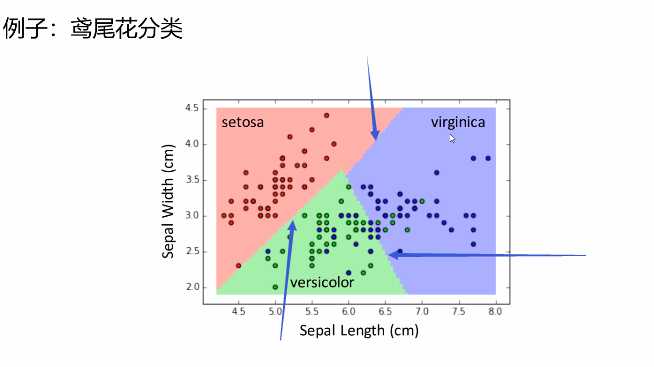
如上图，通过机器的学习确定边界，将新事物放在此维度中，来进行预测或者判断
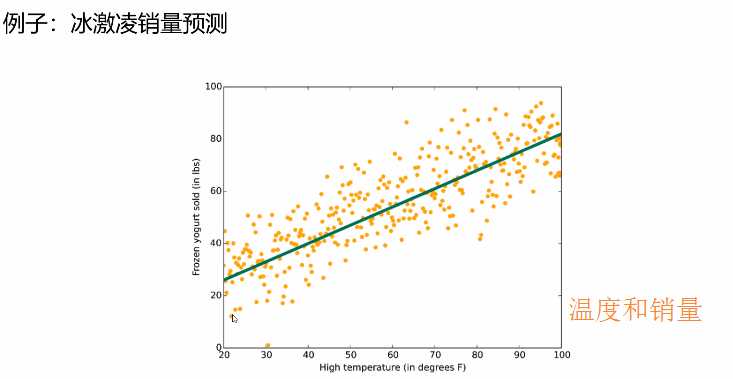
2，回归算法：
应用：预测公司的业务增长量、预测房价等
原理：用属性的历史数据预测未来的趋势；
假设一些已知类型的函数可以拟合目标数据，然后利用某种误差分析确定一个与目标数据拟合程度最好的函数
分类VS回归：
分类模型采用离散预测值（在集合里面的），回归模型采用连续预测值 。看预测的值来进行分类
3，聚类算法：
应用：发现信用卡高级用户、对客户分群达到精确营销的目的
原理：
1，在没有给定划分类的情况下，根据信息相似度进行信息聚类。
2，聚类的输入是一组未被标记的数据，根据样本特征的距离或相似度进行划分。划分原则是保持最大的组内相似性和最小组间相似性
3，挖掘未被标记的样本结构，1) 聚类相似样本，2) 异常样本检测
机器学习按照样本分类：
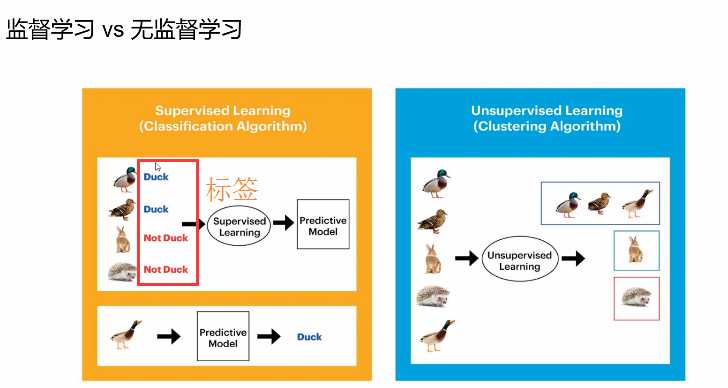
1，监督学习，训练样本包含对应的“标签”，如识别问题（也就是给定的数据外还包括给定的数据标签）
①分类问题，样本标签属于两类或者多类（离散）
②回归问题，样本标签包括一个或多个连续变量（连续）
2，无监督学习，训练样本的属性不包含对应 的“标签”，如聚类问题
线性回归：
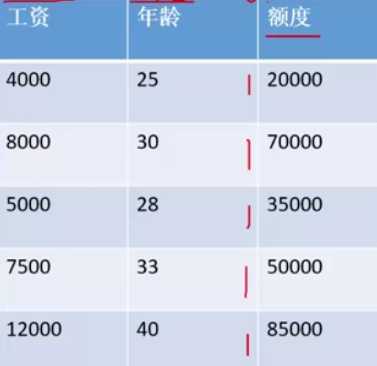
通过上述表中数据来预测年龄和工资对于贷款的影响：
我们把竖向叫做特征、横向叫实例
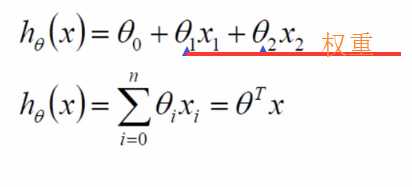
那在这个地方，工资和年龄是两个特征；根据这两个特征得出银行会给贷款多少钱
给定了 具体的额度，也就是这一列就是y，是标签值
x1和x2就代表这两个特征，而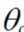
就表示权重系数
默认x0为1
现在需要做一个假设
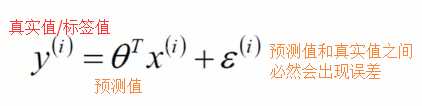
误差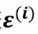
是独立并且具有相同的分布通常认为服从均值为0方差为
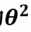的高斯分布
何为相同的分布呢？
何为均值为0？
一条线上下浮动点之间均值不可能百分百为0，但是我们可以上下移动这条线，在一定的范围内可以让上下均值为0，所以做一个均值为0做一个假设
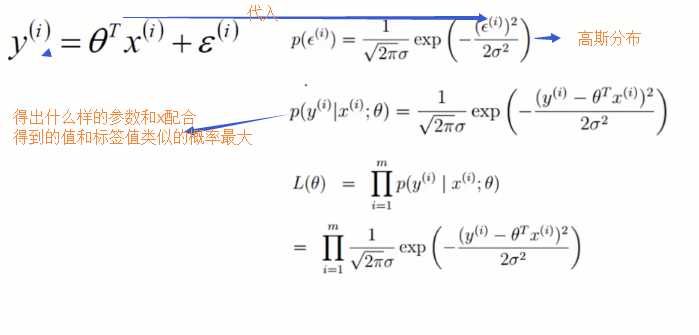
然后对所有的样本进行累乘和，得到的结果自然是越大越好，也就是咱们需要求出什么的参数使得结果最大。
由于累乘法比较麻烦，所以我们引入对数
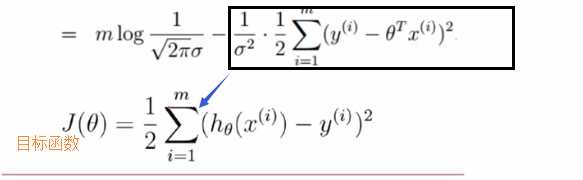
目标函数是越小越好才能让整体概率最大
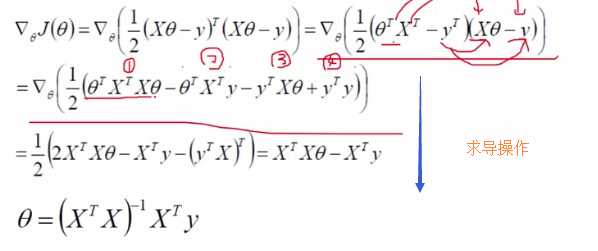
算出极值点，也就是让求导等于0
那在代码中怎么写线性回归呢？
数据集的准备以及划分
样本特征（x）格式
二维数组，形状（n_samples,n_features）
标签（y）格式
一维数组，形状（n_samples）
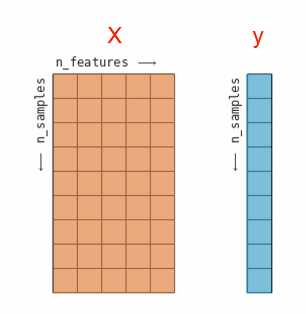
将数据集划分为训练集和测试集
在训练集上训练模型
输入训练数据的特征和标签
在测试集上测试模型
输入测试数据的特征
根据输出的预测标签和真实标签进行比较检验模型的性能
sklearn提供了一个非常便捷的划分函数
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X, y,test_size=1/4,random_state=0)
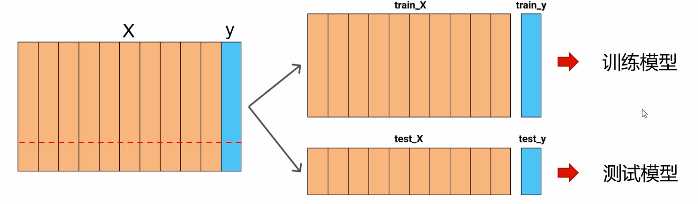
其中X是原来所有数据集的特征矩阵，y对应所有样本的标签，random_state代表随机种子，保证下次运行生成的数据依旧是相同的
import sklearn from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(X, y,test_size=1/4,random_state) from sklearn.neighbors import KNeighborsClassifier # K近邻算法 knn = KNeighborsClassifier（n_neighbors=1） # 设置邻居参数为1 knn.fit(X_train,y_train) # 对训练集进行训练 print("结果为：{:.2f}".format(knn.score(X_test, y_test))) # 通过score方法直接得出准确率
上述的代码片段包含了应用scikit-learn中任何机器学习算法的核心代码。fit，predict和score方法是scikit-learn监督学习模型中最常见的接口。
原文：https://www.cnblogs.com/zhoulixiansen/p/10835869.html